Графика. Окружности: касание, пересечение, связь с другими объектами

Первое решение.

Пусть решение данной системы. Предположим, что тогда тоже решение системы. Кроме того, так как хотя бы одно из чисел не равно (иначе бы то возникают дополнительные пары Но ведь должно же быть два решения, значит, или Тогда разберем случаи.

1.

Получим:

Значит,

2.

Имеем:

Значит,

Заметим, что нет гарантии того, что найденные значения будут подходить под условие задачи, так как мы нашли при условии, что пара вида будет решением. Теперь проверим полученные значения

1.

Тогда Но значит, такое не подходит.

2.

Система принимает вид:

Заметим, что из системы следует, что Значит, Тогда Откуда имеет две пары Значит, такое значение нам подходит.

3.

Система принимает вид:

Заметим, что из системы следует, что Значит, Тогда Откуда имеет две пары Значит, такое значение нам подходит.

Второе решение.
Решим задачу графически. Первое уравнение задает окружность с центром в начале координат и радиусом или пустое множество (при Значит Второе уравнение задает гиперболу, либо совокупность прямых Тогда будет ровно решения, когда окружность касается гиперболы, то есть расстояние от начала координат до графика второго уравнения будет равно

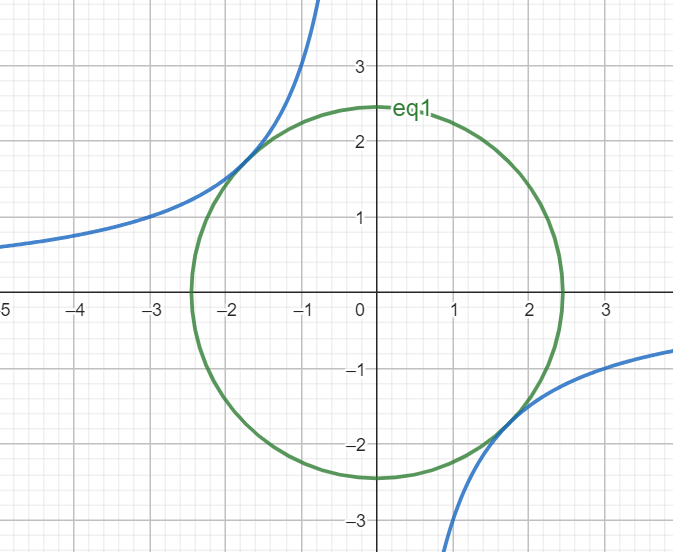
Пусть лежит на гиперболе, тогда

Квадрат расстояния от начала координат до этой точки равно:

Тогда расстояние от начала координат до графика второго уравнения (наименьшее расстояние от начала координат до точки на графике второго уравнения) будет равно Имеем:

Так как то