Графика. Окружности: касание, пересечение, связь с другими объектами

1) . Тогда наше неравенство имеет вид , которое, очевидно, решений не имеет.

2) . Построим графики и . График есть полуокружность с центром в точке в начале координат и радиусом График — прямая. Оба этих график представлены на рисунке:

Решением неравенства будут все точки, при которых график находится выше графика , причем, согласно условию задачи, среди решений должно быть хотя бы одно отрицательное. Это будет в том и только том случае, если прямая будет проходить ниже точки Последнее будет иметь место, если Итак, нам осталось решить неравенство .

Случай 1.

Случай 2

Пусть . Тогда, с учётом допустимых значений , неравенство равносильно системе

Решения этой системы - точки на полуокружности , лежащие ниже графика функции .

При изменении параметра график функции перемещается вдоль оси . При значениях , близких к в качестве множества решений имеем непересекающихся интервала. При значениях , близких к получается интервала.

Крайнее положение графика, при котором получается два интервала, изображено на рисунке:

Координаты точки пересечения окружности и прямой равны

Так как , то .

Таким образом, ответом является множество

Эту задачу неприятно решать алгебраически, поскольку у нас есть знак модуля. С другой стороны, легко понять, как построить график каждого уравнения. Тогда давайте решим эту задачу графически. Второе уравнение представляет из собок пучок прямых, проходящих через точку (1;0). А первое уравнение равносильно системе:

Теперь перепишем первые два условия в другом виде, поделим на 2 третье условие:

Первое условие задает окружность с центром (1; -1) и радиусом 1, второе - окружность с центром (-1; 1) и радиусом , а третье - область «не выше» прямой Тогда график первого уравнения выглядит так:

Тогда нам нужно найти , при которых пересечения графиков обоих графиков есть хотя бы 3.

Заметим, что нам подходят только , при которых прямая будет лежать «между» красной и оранжевой прямой. Красная прямая касается окружности в точке (1;0), а оранжевая прямая - прямая, которая задается уравнением Найдем уравнение красной прямой. Пусть - центр окружности , - точка с координатой (1;0), - точка с координатой (-1;0). Тогда треугольник - прямоугольный, по теореме Пифагора

Так как перпендикулярна к красной прямой, то Значит, ответ к задаче

Первое решение.

Пусть решение данной системы. Предположим, что тогда тоже решение системы. Кроме того, так как хотя бы одно из чисел не равно (иначе бы то возникают дополнительные пары Но ведь должно же быть два решения, значит, или Тогда разберем случаи.

1.

Получим:

Значит,

2.

Имеем:

Значит,

Заметим, что нет гарантии того, что найденные значения будут подходить под условие задачи, так как мы нашли при условии, что пара вида будет решением. Теперь проверим полученные значения

1.

Тогда Но значит, такое не подходит.

2.

Система принимает вид:

Заметим, что из системы следует, что Значит, Тогда Откуда имеет две пары Значит, такое значение нам подходит.

3.

Система принимает вид:

Заметим, что из системы следует, что Значит, Тогда Откуда имеет две пары Значит, такое значение нам подходит.

Второе решение.
Решим задачу графически. Первое уравнение задает окружность с центром в начале координат и радиусом или пустое множество (при Значит Второе уравнение задает гиперболу, либо совокупность прямых Тогда будет ровно решения, когда окружность касается гиперболы, то есть расстояние от начала координат до графика второго уравнения будет равно

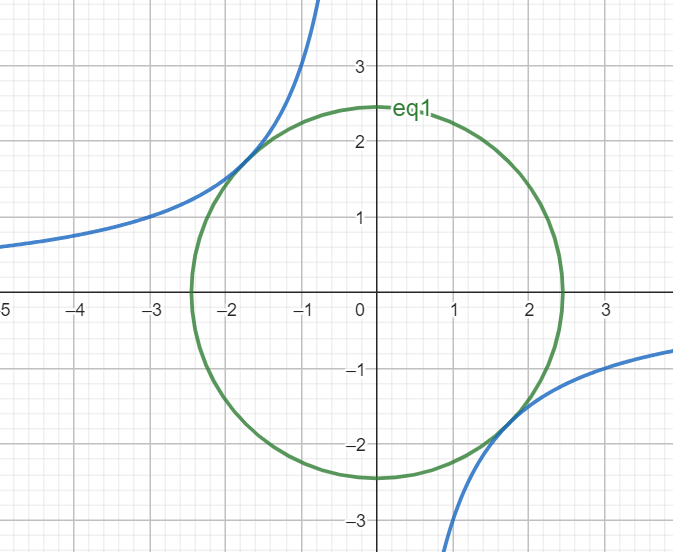
Пусть лежит на гиперболе, тогда

Квадрат расстояния от начала координат до этой точки равно:

Тогда расстояние от начала координат до графика второго уравнения (наименьшее расстояние от начала координат до точки на графике второго уравнения) будет равно Имеем:

Так как то

Второе уравнение системы равносильно совокупности

Эта совокупность задаёт две непересекающиеся окружности и — с центрами в точках и и радиусами и соответственно.

Теперь рассмотрим первое уравнение системы:

Видим, оно определяет прямую с угловым коэффициентом При фиксированном значении — т.е. при фиксированном угле наклона — и при получаем всевозможные прямые с угловым коэффициентом

Чтобы система имела ровно решения, прямая должна пересекать каждую из окружностей ровно в двух точках. Это возможно в том и только том случае, когда угловой коэффициент прямой по модулю меньше, чем угловой коэффициент общей внутренней касательной двух данных окружностей (тогда за счёт выбора параметра можно подобрать такое положение прямой, что она пересекает каждую из окружностей дважды).

Проведём общую внутреннюю касательную к окружностям (пусть и — точки касания этой прямой с и соответственно). Пусть — прямая, параллельная и проходящая через точку пусть также ( поэтому — угол наклона общей внутренней касательной). Так как

а также то из прямоугольного имеем

Значит,

С учётом сказанного выше подходят все значения углового коэффициента, по модулю меньшие, чем откуда

Нарисуем графики неравенств в плоскости Первое неравенство задает множество внутри квадрата со стороной Распишем второе неравенство:

Второе неравенство задает множество точек вне окружности с радиусом Чтобы нарисовать третье неравенство будем использовать метод областей:

Нарисуем эти две прямые и методом областей найдем множество точек, удовлетворяющие третьем неравенству.

В итоге получаем следующую картинку:

Заметим, что нужна нам фигура это треугольник без меньшего сегмента Вычислим площадь треугольника

Высота треугольника совпадает со стороной квадрата и равняется Длина отрезка равняется Тогда площадь равняется

Вычислим площадь сегмента:

Угол радиус окружности тогда площадь сегмента равняется:

Тогда площадь сегмента это разность сектора и треугольника и его площадь:

Тогда искомая площадь равняется:

Перепишем первое уравнение:

При второе уравнение имеет решение , которое не подходит под первое уравнение системы. Заметим, что при перед нами две окружности: с центром радиусом и с центром в радиусом

Условие, что окружности касаются, равносильно тому, что расстояние между центрами равно разности или сумме радиусов. Тогда либо (внутреннее касание), либо (внешнее касание).

Итак, или .

Второе уравнение можно переписать как , это уравнение окружности с центром в и радиусом .

Уравнение симметрично относительно замены на , а при подстановке в систему обнаруживаем, что пара является решением системы при любых значениях параметра.

Нарисуем графики наших уравнений при разных .

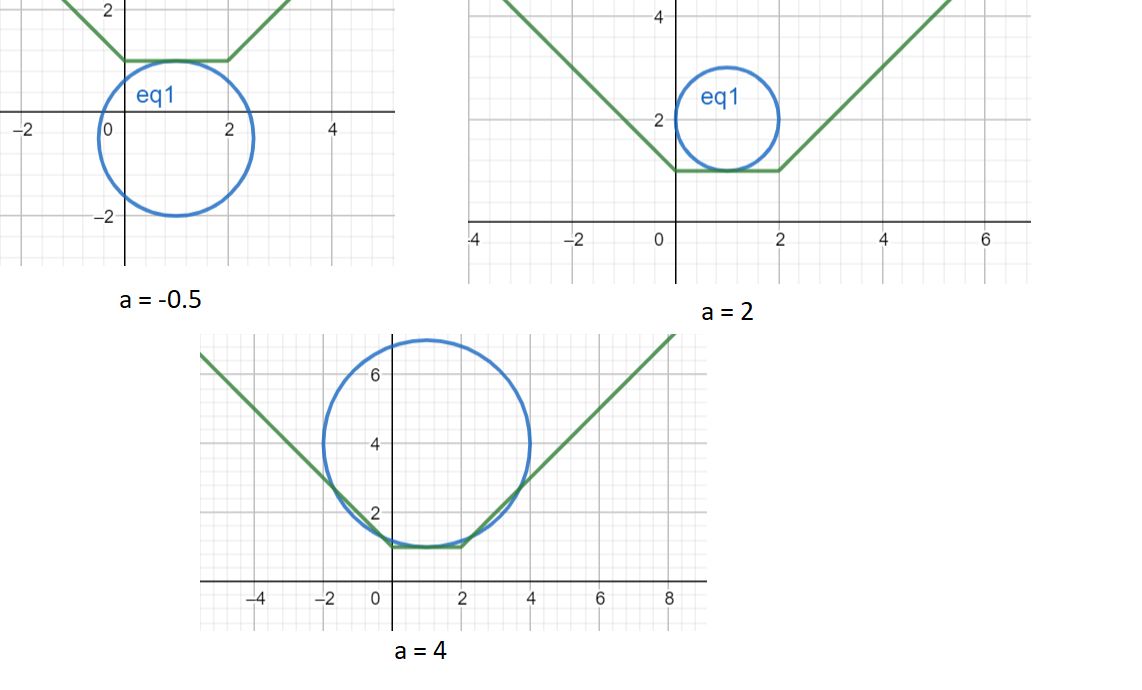
Заметим, что , поэтому если , то

и решение у системы только

Других решений, кроме на отрезке для не может быть, так как в таком случае и опять .

Значит, есть по одному решению при и при (из симметрии). То есть система

должна иметь одно решение.

Заметим, что при эта система имеет одно решение только тогда, когда окружность касается прямой. Иначе если точек пересечений больше одной, то для обеих верно, что , так как и поэтому .

Окружность касается прямой, если они пересекаются в одной точке, так что уравнение имеет одно решение относительно . Дискриминант этого уравнения равен нулю при .

С учётом остаётся Это значение подходит под предыдущие условия и при у системы получится тоже одно решение по симметрии.

В левой части равенства применим формулу синуса двойного угла, а в правой части применим формулу суммы синусов:

Случай 1:

Случай 2:

Семейство горизонтальных прямых на плоскости с уравнениями принадлежат множеству

Случай 3:

Семейство вертикальных прямых на плоскости с уравнениями принадлежат множеству Семейство прямых разбивает плоскость на равные прямоугольные треугольники с катетами и

Радиус круга, вписанного равен Если радиус круга, не имеющего с общих точек, имеет радиус то его центр принадлежит одному из треугольников разбиения, а окружность его границы имеет общие точки со сторонами треугольника. Таким образом, радиус такой окружности меньше радиуса вписанной окружности.

Для начала в силу неотрицательности можем сделать замену , после чего зафиксируем все точки вида на окружности , откуда получим уравнение . Любое решение изначального уравнения будет решением этого для какого-то фиксированного радиуса. То есть остаётся понять, когда есть решения у системы

Решения несложно представить графически, переписав второе, как . Заметим, что ищем мы их только в первой четверти, поэтому при неположительных значениях обязательно откуда — единственное решение, которое, вообще говоря, будет решением для любого значения параметра. Далее

Видно, что “ближайшая точка окружности к прямой” — это , полученная построением перпендикуляра из центра — именно в ней будет происходить касание. Далее при условии можем посчитать

Данное расстояние должно быть больше радиуса, чтобы решений при положительном не оказалось — это нам и требуется. Значит, .

Остаётся последний случай: отрезок прямой лежит внутри окружности, тогда крайний случай — совпадение точки , которая в силу лежит дальше от начала координат с верхней точкой окружности, тогда

после этого отрезок прямой в первой четверти лежит строго внутри окружности и решений при положительном радиусе не будет (то есть меньшие подходят, откуда и получаем ответ).

Первое уравнение системы не меняется при замене на и/или на Следовательно, множество точек, задаваемых первым уравнением симметрично относительно обеих осей координат. В первой четверти получаем часть прямой отрезок, соединяющий точки и Используя симметрию множества относительно координатных осей, получаем ромб вершинами ,

Второе уравнение системы может быть записано в виде Оно задаёт окружность с центром радиуса или точку , если При решений нет, так что рассмотрим случай окружности.

а) И ромб, и окружность симметричны относительно оси абсцисс, следовательно 3 решения возможны только в том случае, когда одна из общих точек окружности и ромба лежит на оси абсцисс. Это происходит, если радиус окружности равен отрезку или отрезку , т.е. или Несложно видеть, что при система имеет 3 решения, а при решений. Значит, 3 решения возможны только при

б) Пусть – радиус той окружности, которая касается сторон и , a радиус той окружности, которая касается сторон и ромба. Система имеет ровно два решения в том и только том случае, когда . Пусть окружность радиуса касается стороны в точке , а окружность радиуса касается стороны в точке Треугольник прямоугольный, равен угловому коэффициенту прямой , т.е. Тогда По теореме Пифагора для треугольника получаем , откуда Поскольку треугольники и подобны и коэффициент подобия равен , то Окончательно получаем

Второе неравенство равносильно системе неравенств

Значит, исходная система равносильна следующим:

Множества точек, задаваемых этими неравенствами на плоскости и при этом выступают в роли параметров), - это круги радиуса с центрами соответственно. Условие задачи означает, что полученная система должна иметь решение относительно , то есть все три круга должны иметь по крайней мере одну общую точку.

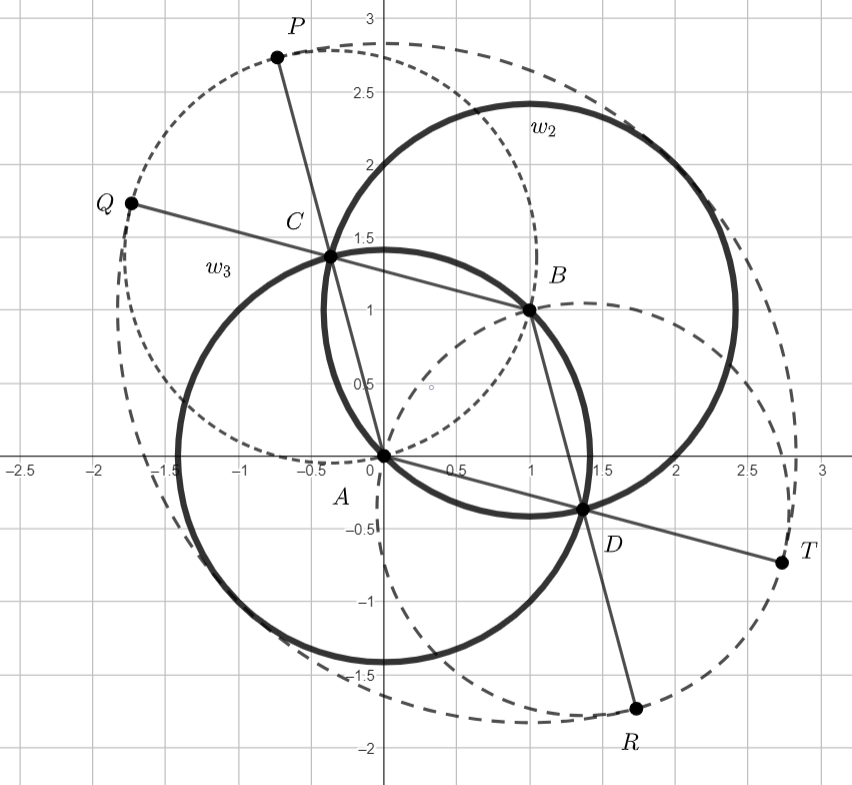
Пусть окружности, ограничивающие и , пересекаются в точках и (тогда треугольники и - равносторонние). Пересечение кругов и есть фигура , представляющая собой совокупность двух меньших сегментов этих кругов, ограниченных хордой . Тогда фигура состоит из всевозможных точек , находящихся на расстоянии не более от фигуры . (Это совокупность всех кругов радиуса , центры которых принадлежат фигуре .)

Пусть точки и симметричны точкам и (соответственно) относительно точки ; точки и симметричны точкам и (соответственно) относительно точки .

А само множество есть объединение следующих четырёх секторов (центральный угол всех секторов меньше ):

• сектор круга с центром в точке и радиуса
• сектор круга с центром в точке и радиуса
• сектор круга с центром в точке и радиуса
• сектор круга с центром в точке и радиуса

Заметим, что первые два сектора пересекаются по ромбу , и никаких других пересечений между секторами нет. При этом первые два сектора равны между собой, и последние два сектора также равны между собой. Таким образом, площадь фигуры равна

Изображено множество точек (в плоскости (𝑎; 𝑏), удовлетворяющих второму неравенству системы – 2 балла; указано (или изображено, описано) множество решений первого неравенства – баллы не добавляются; верно описан способ построения фигуры 𝑀 (например, совокупность кругов заданного радиуса, центры которых лежат в некотром множестве), но сама она построена неверно – 1 балл; изображена фигура 𝑀 – 3 балла; найдена её площадь – 2 балла. Если фигура 𝑀 изображена неверно, нахождение площади не оценивается, и за задачу ставится не более 3 баллов. Если фигура 𝑀 представляет собой пересечение двух кругов с центрами 𝐴 и 𝐵 радиусов 2𝐴𝐵, за задачу ставится 3 балла (при этом не играет роли, найдена ли площадь)

Запишем ОДЗ:

Видно, что если то решений нет, поэтому пусть

Получаем, что принадлежит пересечением отрезков и

Заметим, что

Стало быть, графики функций и — верхние половины окружностей радиуса 2 с центрами в точках и соответственно. График же функции — верхняя половина окружности радиуса с центром в точке Первые две полуокружности имеют одну общую точку —

Рассмотрим несколько случаев: 1) При третья полуокружность первые две не пересекает и решение будет одно.

2) При третья полуокружность пересекает первые две в точках с абсциссами из отрезка

3) При точки пересечения совпадают.

4) При третья полуокружность либо пересекает первые две в точках с абсциссами по модулю большими 1, либо не пересекает вообще.

Стало быть, решение будет единственным при

Рассмотрим первое уравнение системы и изобразим множество его решений на координатной плоскости. Для раскрытия модулей найдём множества точек, в которых выражения под модулями обращаются в ноль. Это прямые и . Они делят плоскость на 4 части, и в каждой из этих частей знаки выражений под модулями постоянны. Чтобы их определить, можно выбрать в каждой из четырёх частей по точке и найти знаки выражений в этих точках. Возьмём область, расположенную снизу от обеих прямых. В ней лежит, например, точка . Подстановкой несложно убедиться, что в этой точке оба выражения и отрицательны. Таким образом, уравнение принимает вид , откуда . C учётом рассматриваемых ограничений подходит отрезок с концами в точках и . Аналогично рассматриваем остальные три случая, и в итоге получаем границы квадрата с вершинами в точках и . Эта фигура не имеет пересечения с полуплоскостью , поэтому можно считать, что . С учётом указанного замечания второе уравнение можно записать в виде (опустив модуль у переменной . Обозначим множество точек, определяемых этим уравнением, через . Если , у уравнения нет решений. При оно задаёт две точки и (-4;3). Поскольку обе они не принадлежат квадрату , система не имеет решений, и значение не удовлетворяет условию задачи. Перейдём к случаю .

При уравнение принимает вид , и мы получаем окружность радиуса с центром в точке (или её часть, лежащую в полуплоскости , если вся она в этой полуплоскости не помещается). Поскольку уравнение инвариантно относительно замены на , множество симметрично относительно оси . Таким образом, есть совокупность полученной выше окружности (или её части) и окружности, получающейся из уже построенной отражением относительно оси

Если , график не пересекает квадрат , и система уравнений не имеет решений. Если , система уравнения имеет два решения - точки и . Если , дуга окружности пересекает отрезок дважды эти две точки, а также им симметричные относительно оси , образуют 4 различных решения системы. Если , дуга окружности пересекает отрезки и в двух точках с положительной абсциссой. Аналогично, эти две точки, а также им симметричные относительно оси Оy, образуют 4 различных решения системы. Если 25 , система уравнений имеет два решения - точки и . Наконец, если , дуга окружности не пересекает стороны квадрата и система уравнений не имеет решений. Таким образом, система уравнений имеет ровно два решения только при и .

Рассмотрим второе уравнение системы. При оно принимает вид и мы получаем часть окружности радиуса с центром в точке , лежащую в первой четверти. При замене на множество точек заданное уравнением системы, симметрично относительно оси ординат, а при замене на — относительно оси абсцисс. Значит, график уравнения состоит из четырёх дуг окружностей и начала координат

Первое уравнение перепишем в виде Оно определяет окружность радиуса с центром в точке В зависимости от значения центр окружности перемещается по прямой

Система имеет два решения тогда и только тогда, когда эта окружность имеет ровно две общие точки с множеством, заданным вторым уравнением. Это возможно при

Рассмотрим второе уравнение системы. Оно инвариантно относительно замены на и/или на . Это означает, что множество точек, задаваемых этим уравнением, симметрично относительно обеих осей координат. В первой четверти (включая её границы), раскрывая модули, мы получаем . Это уравнение задаёт окружность с центром (4; 3) радиуса 5. В первой четверти лежит дуга этой окружности и точка (0; 0). Отображая эту дугу симметрично относительно начала координат и обеих координатных осей, получаем множество точек, задаваемых вторым уравнением (см. рисунок).

Геометрическое место точек, заданных первым уравнением, представляет собой совокупность двух лучей и с началом в точке соответствующие и . Отметим, что луч является частью прямой при любом и не пересекается с полуплоскостью . Этот луч либо пересекает график второго уравнения системы в точке (8; 6), либо не пересекает его вовсе. Последний случай не подходит, т.к. при нём луч пересекает график второго уравнения не более чем в двух точках. Таким образом, для того чтобы система имела три решения, необходимо, чтобы луч пересекал график второго уравнения два раза, а луч — один раз.

Рассмотрим положения луча при различных . Если , луч пересекает только дугу окружности, лежащую во второй четверти (назовём её ). Если , луч дополнительно проходит через точку (0, 0) и имеет два пересечения с графиком второго уравнения. Если , луч проходит через точку (0; 6), принадлежащую графику второго уравнения, а также пересекает дугу . При луч пересекает график второго уравнения трижды: дважды он пересекает дугу , а один раз – дугу, лежащую в первой четверти. При луч касается дуги и пересекает дугу окружности в первой четверти (это значение параметра найдено ниже). Наконец, при луч может пересечь только дугу окружности, лежащую в первой четверти, и общее количество точек пересечения графиков не превосходит двух.

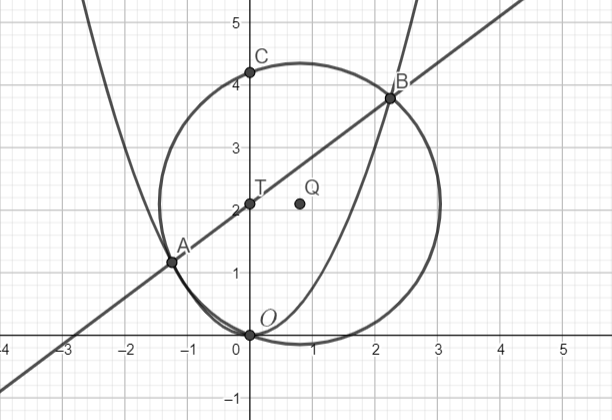
Рассмотрим сначала . Обозначим начало координат через , центр окружности через (так как он лежит на прямой , его ордината равна ; точки пересечения прямой с параболой через и . Пусть также — точка пересечения данной прямой с осью ординат, — точка пересечения окружности с осью ординат, отличная от .

Треугольник равнобедренный как радиусы), — его высота, следовательно, также и медиана, , поэтому точка имеет координаты . Опустим из точки перпендикуляр на ось ординат. Тогда есть угол наклона прямой, его тангенс равен . Отсюда . Аналогично находим, что .

и — две хорды данной окружности. По теореме о пересекающихся хордах , т.е. . Абсциссы и точек пересечения прямой и параболы определяются уравнением . По теореме Виета . Значит, , откуда .

Значение не подходит, так как при этом заданная прямая принимает вид , т.е. проходит через начало координат.

При (естественно, мы рассматриваем только те , при которых прямая и парабола имеют две точки пересечения) оба числа и положительны. Точка является серединой отрезка OC (сохраняем все обозначения первого случая). Тогда с одной стороны выходит, что точка — середина хорды , т.е. лежит внутри окружности. С другой стороны, точки и лежат на окружности, поэтому является хордой этой окружности, а точка лежит на продолжении хорды , т.е. вне окружности. Получаем противоречие, и этот случай невозможен.

Выделим полные квадраты

Каждое из этих уравнений задаёт окружность радиуса 13; у первой из них центром является точка , а у второй - точка .

Если эти уравнения задают одну и ту же окружность, то на этой окружности найдутся точки на расстоянии 10 друг от друга, поскольку диаметр окружности больше . Окружности совпадают в случае, когда у них одинаковые центры. Получаем

Эти равенства выполняются, если либо , либо . В первом случае получаем . Во втором случае , здесь решений нет.

Пусть теперь рассматриваемые окружности различны и пересекаются в точках и . Тогда четырёхугольник - ромб. Известно, что в любом параллелограмме сумма квадратов диагоналей равна сумме квадратов всех четырёх сторон, откуда . Так как мы хотим, чтобы точки и располагались на расстоянии 10 друг от друга, , поэтому . Итак, необходимо, чтобы расстояние между центрами окружностей и было равно 24. Отсюда

Заметим, что первое уравнение при замене на или на не меняется. Тогда график этого уравнения симметричен относительно обеих координатных осей. При и это уравнение имеет вид — луч с началом в точке и угловым коэффициентом Используем симметрию и строим график этого уравнения, получаем два угла: с вершиной в точке и с вершиной в точке и угловыми коэффициентами лучей

Во втором уравнении выделим полный квадрат Тогда это уравнение можно записать так:

Оно задает окружность с центром в точке и радиусом (в случае — это точка ).

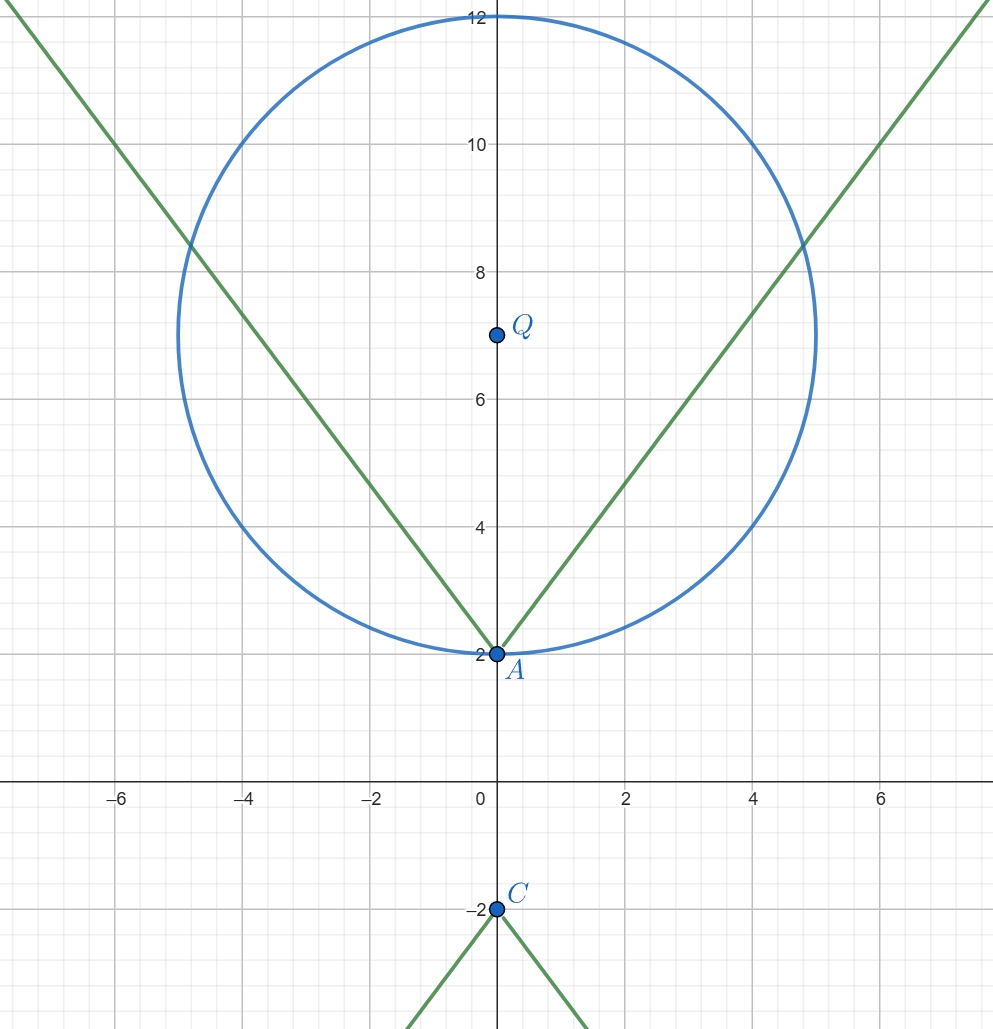
(a) Окружность и график первого уравнения симметричны относительно оси Тогда три решения возможны только в том случае, когда одна из их общих точек лежит на оси этой оси. Это происходит, если радиус окружности равен отрезку или отрезку Так как и то получаем или Видно, что при этих есть еще две общие точки со сторонами угла с вершиной в точке поэтому любое или подходит.

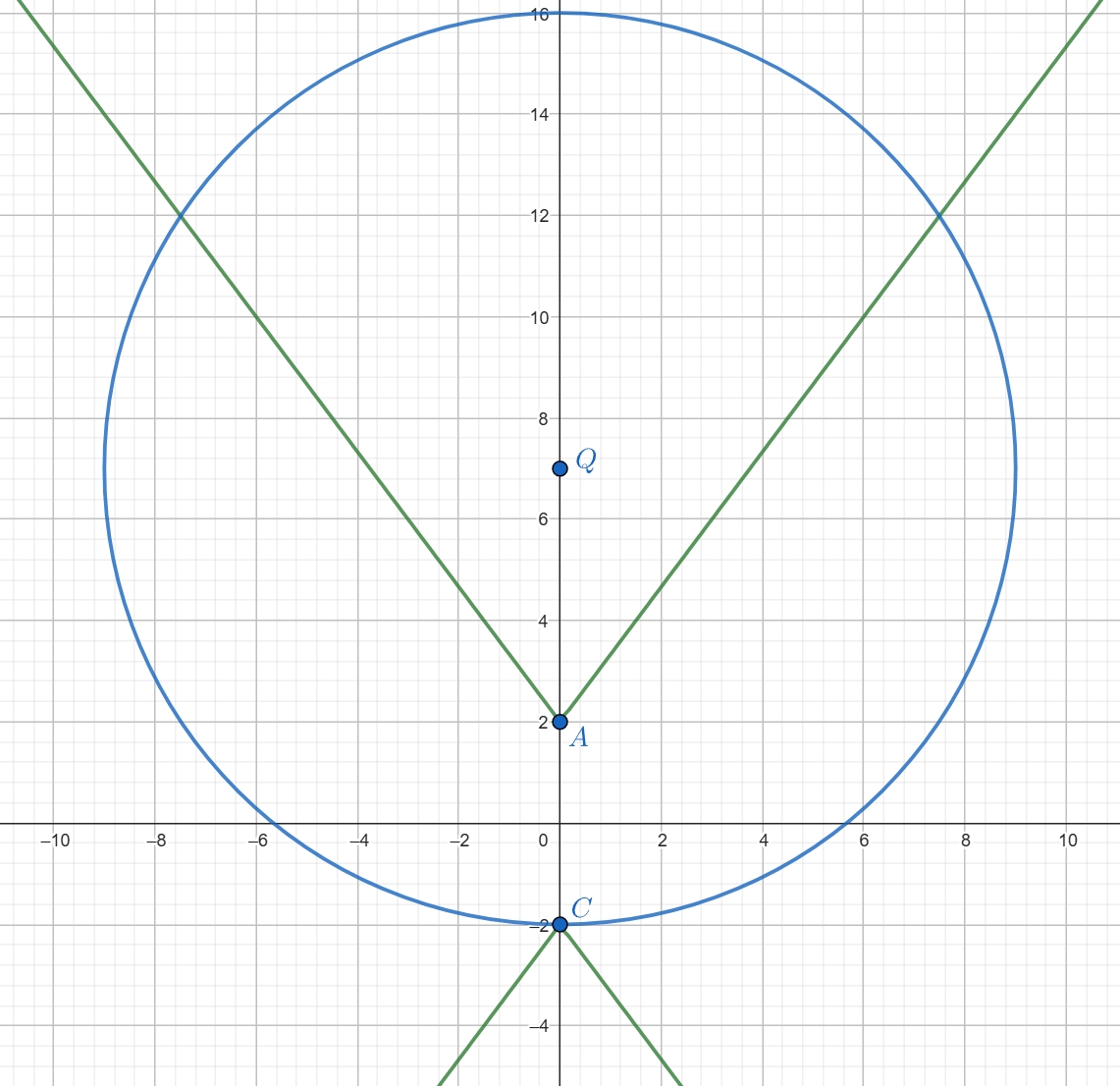
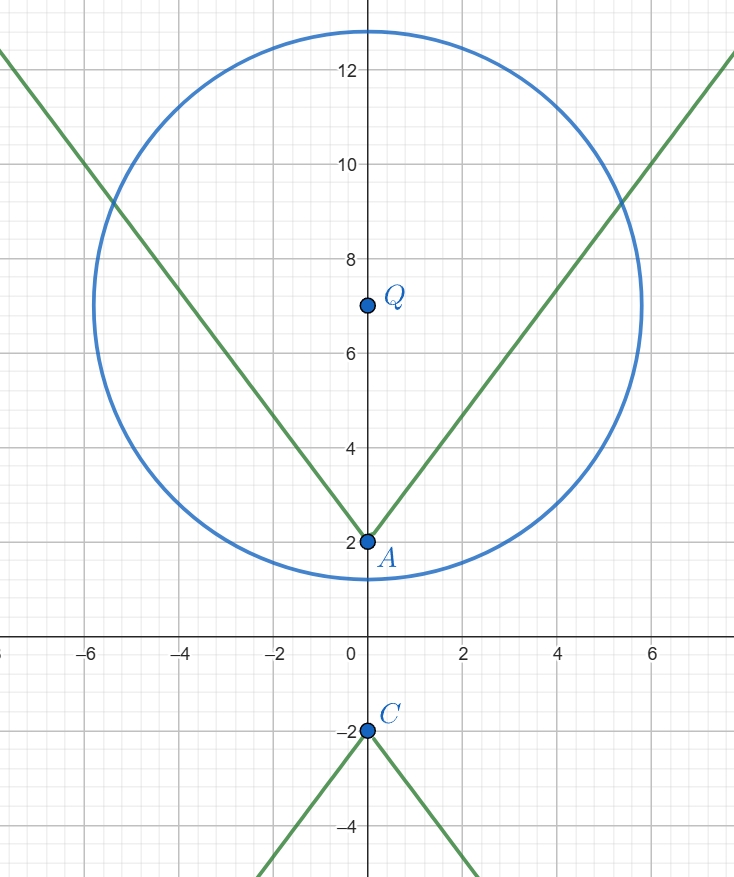
(b) Система дает два решения, если окружность касается угла с вершиной или имеет радиус, больший но меньший Мы уже знаем и так что осталось найти этот радиус (обозначим его ). Для этого опустим перпендикуляр на сторону угла с вершиной в точке Пусть — угол наклона прямой ( Тогда Так как то По теореме Пифагора для получаем Тогда

Рассмотрим неравенство данной системы. При любом значении параметра расстояние от начала координат до прямой равно а точка удовлетворяет этому неравенству. Значит, неравенство задаёт полуплоскость, содержащую точку границей которой является прямая, касающаяся окружности

Уравнение данной системы можно преобразовать к виду Оно задаёт окружность с центром радиуса или точку при

Для того, чтобы система имела решение при любом значении параметра требуется, чтобы окружность пересекала любую из полуплоскостей, определяемых неравенством системы. Пусть радиус той окружности которая касается окружности внешним образом. Тогда сформулированному условию удовлетворяют все значения радиуса из промежутка .

Для окружностей, касающихся внешним образом, сумма радиусов равна расстоянию между центрами. Отсюда получаем, что поэтому а значит .