Графика. Функции с модулем: галочка, корыто и другие

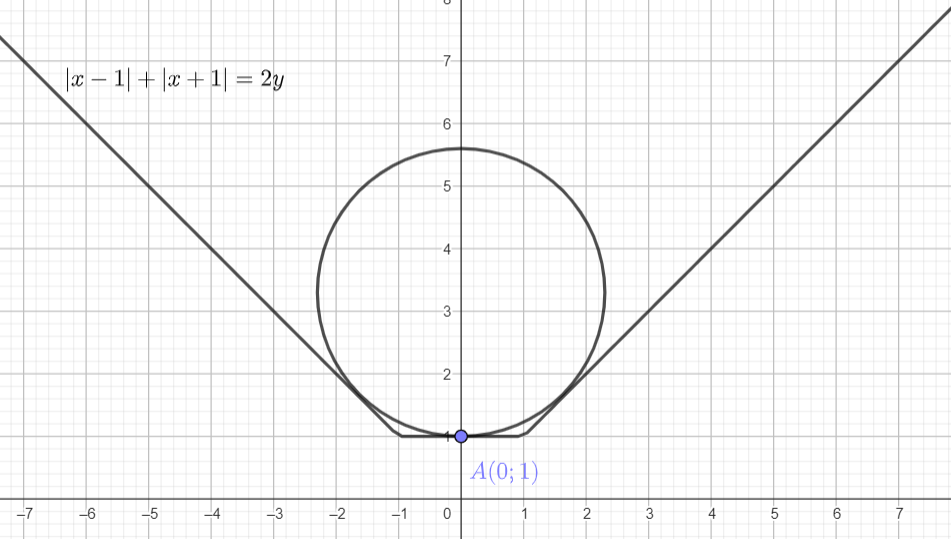
Первое уравнение системы можно записать в виде

Второе уравнение системы преобразуется к виду и является уравнением окружности с центром в точке и радиусом . Эта окружность при любом значении проходит через точку и касается прямой Если то окружность лежит ниже прямой и данная система в этом случае имеет единственное решение При окружность вырождается в точку т. е. в этом случае система тоже имеет единственное решение Если же то окружность расположена выше прямой и система кроме решения будет иметь ещё два решения (симметричных относительно прямой в том случае, когда окружность касается прямых и Это означает, что система

имеет единственное решение, т. е. уравнение имеет единственный корень. Это уравнение можно записать так откуда т. е. Так как то получаем