Графика. Отрезок, ромб, квадрат
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых система уравнений
имеет ровно три решения.
Источники:
Подсказка 1
x² + y² = 3 - это окружность с центром в начале координат и радиусом корень из 3, выражение с модулями - график квадрата с центром в (-2, -9) и длиной диагонали 4, а график второго уравнения системы - окружность с центром в (-2, -4) и радиусом корень из a. А что же является решением системы?
Подсказка 2
Так как нам достаточно, чтобы решение обнуляло хотя бы одну из скобок первого уравнения (а оно будет обнулять ровно одну, так как графики этих скобочек не пересекаются (можно убедиться на чертеже)), значит, решениями будут все пересечения графика второго уравнения с графиками двух скобочек! Какие особенные точки пересечения нужно рассмотреть, чтобы решений было ровно 3?
Подсказка 3
Точки касаний окружности (второе уравнение) с окружностью с центром в начале координат (причём нужно рассмотреть и внешнее, и внутреннее!), а также случай, когда вершины квадрата лежат на окружности с радиусом корень из a(и только они!), именно тогда решений будет три) Осталось лишь вычислить эти точки!
При второе уравнение имеет не больше одного решения, а значит, и вся система иметь трёх решений не может. При
второе
уравнение задаёт окружность с центром
и радиусом
График первого уравнения — объединение окружности с центром
и радиуса
и квадрата с центром
и длиной диагонали
.
Расстояния от центра второй окружности до углов квадрата по прямой равны
и
, а до центра другой окружности
. Мы хотим три точки пересечения с областью решений первого уравнения, поэтому либо окружность с параметром
проходит через обозначенные углы квадрата (иначе пересечений с ним чётное число), либо касается окружности с центром в начале
координат.
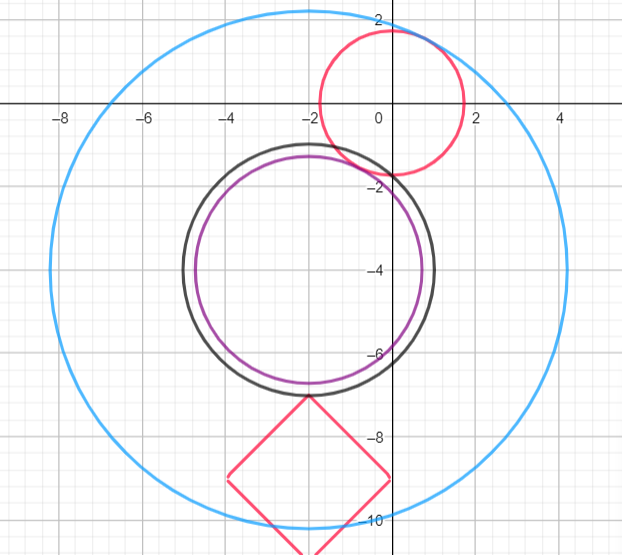
Замечание. Далее цвета окружностей названы в соответствием отображением в светлой, а не тёмной теме на сайте :)
- Касание происходит внешним образом и
, то есть нет пересечений с квадратом (фиолетовая окружность) и пересечение всего одно.
(проходит через вершину квадрата), как раз три точки пересечения, поскольку с красной ровно две точки пересечения (чёрная окружность).
. Здесь также три решения (синяя окружность).
, не пересекает красную окружность, потому решение всего одно.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




