Касательные к сфере (+ каркасный тетраэдр)

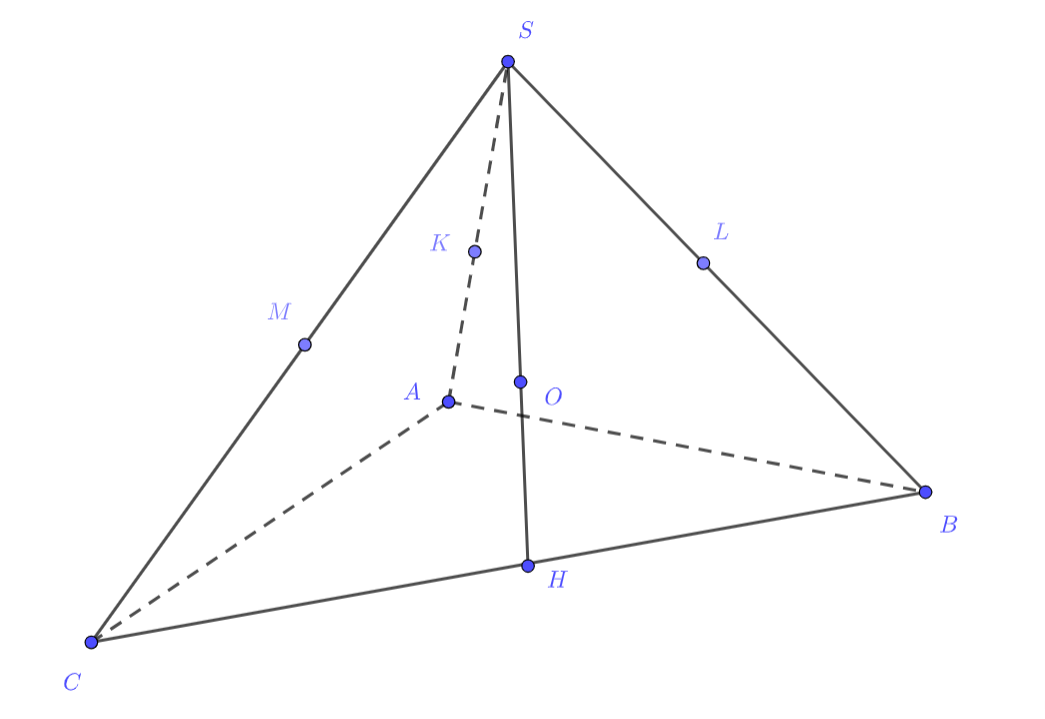
Пусть — центр сферы — основания перпендикуляров, опущенных из точки на ребра соответственно; — высота пирамиды и — радиусы сфер и соответственно.

a) Поскольку точка лежит на серединном перпендикуляре к отрезку она равноудалена от концов этого отрезка, т.е. Аналогично и Значит, поэтому точка является центром сферы . Следовательно, расстояние между центрами сфер равно нулю.

b) Из равенства прямоугольных треугольников , и — общая сторона) следует, что Поскольку точки — это середины боковых рёбер пирамиды, отсюда получаем, что боковые рёбра равны между собой. Тогда высота пирамиды проходит через центр окружности, описанной около основания (действительно, по катету и гипотенузе, откуда ). Но в пирамиде боковые рёбра также равны между собой как радиусы сферы ; значит, и её высота, проведённая из вершины проходит через центр окружности, описанной около основания. Таким образом, высота пирамиды проходит через точку Кроме того, точка является центром окружности, описанной около основания. Поскольку треугольник прямоугольный, — это середина гипотенузы Так как отрезок перпендикулярен плоскости основания, он равен радиусу сферы

Для нахождения соотношения между радиусами рассмотрим прямоугольный треугольник Точка — середина гипотенузы на катете находится точка причём , Треугольники , и равны по катету и гипотенузе, следовательно, Значит, Тогда из треугольника находим, что

c) поэтому треугольник — равносторонний, B равнобедренном треугольнике известны боковые стороны и угол при основании Отсюда находим, что . По теореме Пифагора для треугольника находим, что поэтому объём пирамиды равен