Касательные к сфере (+ каркасный тетраэдр)
Ошибка.
Попробуйте повторить позже
Сфера касается всех рёбер пирамиды, в основании которой лежит выпуклый 2024-угольник. Покрасим в шахматном порядке углы между последовательными рёбрами при вершине вне многоугольника в синий и красный цвета. Докажите, что произведение синусов половинок синих углов равно произведению синусов половинок красных.
Источники:
Подсказка 1
Пусть в основании пирамиды лежит 2024-угольник А₁А₂…А₂₀₂₄, а О – её вершина. Для начала будет полезно определиться, что синих и красных углов будет равное количество, так как в пирамиде у нас чётное число боковых граней. Давайте рассмотрим одну боковую грань и попробуем найти синус нужного нам угла. Обратите внимание: нас просят найти синус от половинного угла грани. На какую формулу это может быть намеком?
Подсказка 2
Действительно, просто так искать синус половинного угла мы не очень умеем. Давайте рассмотрим квадрат синуса половинного угла и понизим его степень. sin²(α/2) = (1 – cos(α)) / 2. А вот cos(α) мы уже умеем находить, например, по теореме косинусов. Но мы всё ещё никак не использовали нашу сферу. Как может помочь то, что она касается всех ребер пирамиды?
Подсказка 3
Если сфера касается всех ребер, значит, в пересечении с нашей боковой гранью будет получаться окружность, вписанная в треугольную боковую грань пирамиды. Пускай такая окружность касается стороны OА₁ в точке B₁, стороны OА₂ - в точке B₂, а стороны А₁А₂ - в точке С₁. Тогда по теореме об отрезках касательных к окружности, проведенных из одной точки, А₁B₁ = А₁С₁ = x, А₂B₂ = А₂С₁ = y, OB₁ = OB₂ = z. Как тогда выражается sin²(α/2) через x, y, z?
Подсказка 4
Давайте воспользуемся теоремой косинусов для треугольника А₁А₂O, но выразим стороны через x, y, z. Чему тогда будет равно (1 – cos(α)) / 2?
Подсказка 5
После преобразований получаем sin²(α/2) = (А₁B₁* А₂B₂) / (OА₁ * OА₂), где α = ∠А₁OА₂. Заметьте, что данная формула будет верна, как для красных, так и для синих углов, если вместо 1 подставить i, а вместо 2 – (i + 1). Объясните, почему в таком случае произведение синих углов будет равно произведению красных.
Пусть в основании пирамиды лежит 2024-угольник , точка
— вершина пирамиды. Пусть для всех
, сфера
касается ребер
в точке
, а ребер
в точке
(
).
Рассмотрим треугольник . Сечением сферы в его плоскости является вписанная в него окружность, которая касается его сторон
в точках
,
,
. Пусть
Из теоремы косинусов имеем
Как известно,
По условию достаточно показать, что произведения квадратов половинных синих и половинных красных углов равны. Но из равенства
выше каждое из таких произведений равно произведению отношений для всех
, что доказывает исходное
равенство.
Ошибка.
Попробуйте повторить позже
Длина ребра куба равна 1. Найдите радиус сферы, проходящей через точку
и касающейся прямых
и
.
Источники:
Подсказка 1
Тут у нас и параллельные прямые, и биссектрисса - давайте поищем равные углы. Помним, что биссектрисса отсекает от параллелограмма равнобедренный треугольник.
Подсказка 2
Верно, получаем MCK равнобедренный. Тогда ОС (где О - центр окружности) - серединный перпендикуляр КМ, а треугольники KOC и МОС равны и равнобедренны. На этом этапе давайте остановимся в изучении чертежа и подумаем, как нам доказать требуемое. Какой признак может указывать на принадлежность точки О описанной окружности BCD?
Подсказка 3
Конечно, в нашем случае проще всего будет доказывать через равенство вписанных углов. Для каких двух углов будет удобнее это доказать?
Подсказка 4
Конечно, легче находится, что OBC и ODC равны и опираются на дугу ОС. Это несложно вывести, если увидеть равенство треугольников BKO и DCO. Теперь остаётся только последовательно всё доказать
Введём декартову систему координат с центром в точке , ось абсцисс — луч
, ось ординат — луч
, ось аппликат — луч
.
Пусть — проекция центра сферы на грань
куба. Определим ее местоположение. Так как сфера касается прямых
и проходит через точку
, то расстояние от точки
до прямых
и
и точки
одинаково (обозначим его
).
Тогда
лежит на луче
, который является биссектрисой угла
. Осталось учесть условие, что центр сферы
касается прямой
, то есть нужно проверить, что расстояние от центра до прямой
совпадает с радиусом сферы
.
Заметим, что есть два случая расположения точки (на рисунке показаны разными цветами):
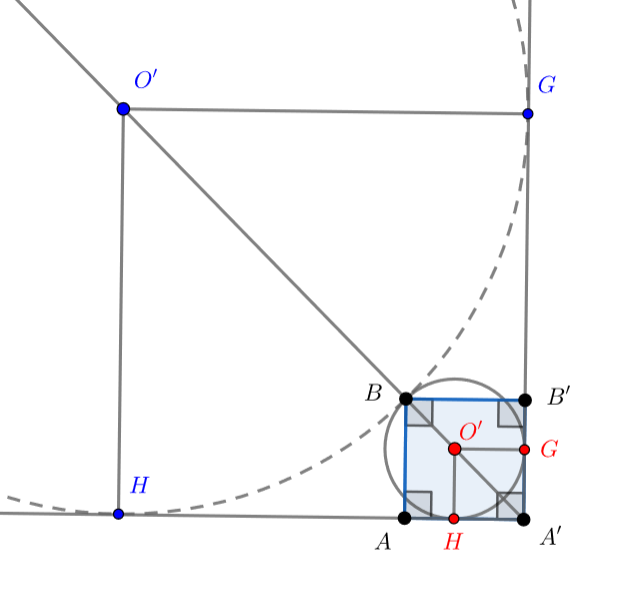
Случай 1: точка лежит на диагонали
.
Тогда из теоремы Пифагора для прямоугольного треугольника получим:
, откуда
. Значит,
центр сферы
имеет координаты
.
Расстояние до прямой равно
. То есть радиус
Случай 2: точка лежит на продолжении луча
.
Тогда из теоремы Пифагора для прямоугольного треугольника получим:
, откуда
. Значит,
центр сферы
в этом случае имеет координаты
.
Расстояние до прямой равно
. То есть радиус
Ошибка.
Попробуйте повторить позже
В основании прямой призмы лежит ромб со стороной 3. Найдите объём призмы, если известно, что существует сфера радиуса 1, касающаяся плоскости нижнего основания, двух противоположных боковых рёбер и всех рёбер верхнего основания.
Источники:
Подсказка 1
Построим чертёж! Проведите перпендикуляры из центра сферы к параллельным между собой боковым рёбрам (в точки касания). Что можно сказать о фигуре, образованной диагональю ромба, частями этих рёбер и проведёнными перпендикулярами?
Подсказка 2
Теперь мы знаем диагональ ромба! Это позволяет нам полностью обсчитать ромб, найти его углы/высоту/площадь и всё что нам нужно!
Подсказка 3
Спроецируем радиус сферы, проведённый в точку касания её с ребром верхнего основания, на плоскость основания. Эта проекция — половина высоты ромба.
Подсказка 4
Работа с теоремой Пифагора поможет нам отыскать оставшуюся часть высоты призмы. Осталось подставить числа в формулу и записать ответ.
Пусть дана призма
— центр данной сферы, которая касается боковых рёбер
и
в точках
и
Заметим, что и
следовательно
А раз
и все четыре точки
лежат в
одной плоскости, то
и
— прямоугольник, значит,
при этом
как диаметр данной
сферы.
Рассмотрим треугольник и найдём высоту
По формуле Герона
тогда
Проецируем на нижнее основание, обозначим проекцию на
она будет являться серединой
Пусть
— точка касания сферы
с
а
— её проекция на нижнее основание.
![]()
Раз , то в силу ТТП и свойств проекции
Тогда
— средняя линия в треугольнике
следовательно
Рассмотрим прямоугольную трапецию в ней
и
Пусть
тогда по теореме
Пифагора
Теперь зная это, посчитаем объём призмы
Ошибка.
Попробуйте повторить позже
Дана треугольная пирамида медианы
и
треугольника
пересекаются в точке
Сфера
касается ребра
в точке
и касается плоскости основания пирамиды в точке
лежащей на отрезке
Сфера
пересекает отрезок
в точках
и
Известно, что
площадь треугольника
равна
а) Найдите произведение длин медиан и
б) Найдите двугранный угол при ребре пирамиды, если дополнительно известно, что
касается грани
в точке
а радиус сферы
равен 5.
Источники:
Пункт а), подсказка 1
Давайте просто начнём хоть что-нибудь делать в задаче и в дальнейшем посмотрим, что из этого получится. У нас есть касание со сферой и секущая. Какой тогда факт связанный со сферой можно сразу заметить?
Пункт а), подсказка 2
Верно, можем записать два выражения по теореме о касательной и секущей. Какую тогда пару равенств отрезков мы получаем?
Пункт а), подсказка 3
Точно, тогда у нас равны произведения в соотношениях, откуда равны SL и MK, а также AM и SA. Но мы знаем, что SA=12 и BC=12. Давайте не будем забывать, что у нас проведены медианы в основании треугольника. Какие тогда ещё отрезки можно найти и какой сделать вывод про треугольник BMC?
Пункт а), подсказка 4
Верно, MA₁=6 по свойству точки пересечения медиан. Но тогда MA₁=BA₁=CA₁=6, и треугольник BMC прямоугольный. Далее, зная площадь треугольника ABC, найти произведение двух оставшихся медиан несложно, так как катеты и будут частями исходных медиан.
Пункт б), подсказка 1
Раз нам нужен двухгранный угол, нужно его сначала построить. Из какой тогда точки удобнее всего опустить перпендикуляр на ребро BC для достижения цели?
Пункт б), подсказка 2
Верно, опустим перпендикуляр KH из точки K. Но тогда, применяя несколько раз теорему о трёх перпендикулярах, получаем, что NH ⊥ BC. Значит нам нужно искать ∠NHK. Но из-за равенства двух прямоугольных треугольников, ∠NHK = 2∠OHK, где O — центр сферы. Чтобы найти угол, скорее всего, надо будет найти сторону прямоугольного треугольника. Но её мы пока не знаем... Какой дополнительное построение тогда можно сделать, где нам что-то известно?
Пункт б), подсказка 3
Верно, давайте проведём ещё высоту в треугольнике BMC, которую мы можем найти. А также у нас два треугольника подобны. Осталось только до конца воспользоваться равенством касательных к сфере, после чего найти неизвестный катет, и, следовательно, двухгранный угол.
а)
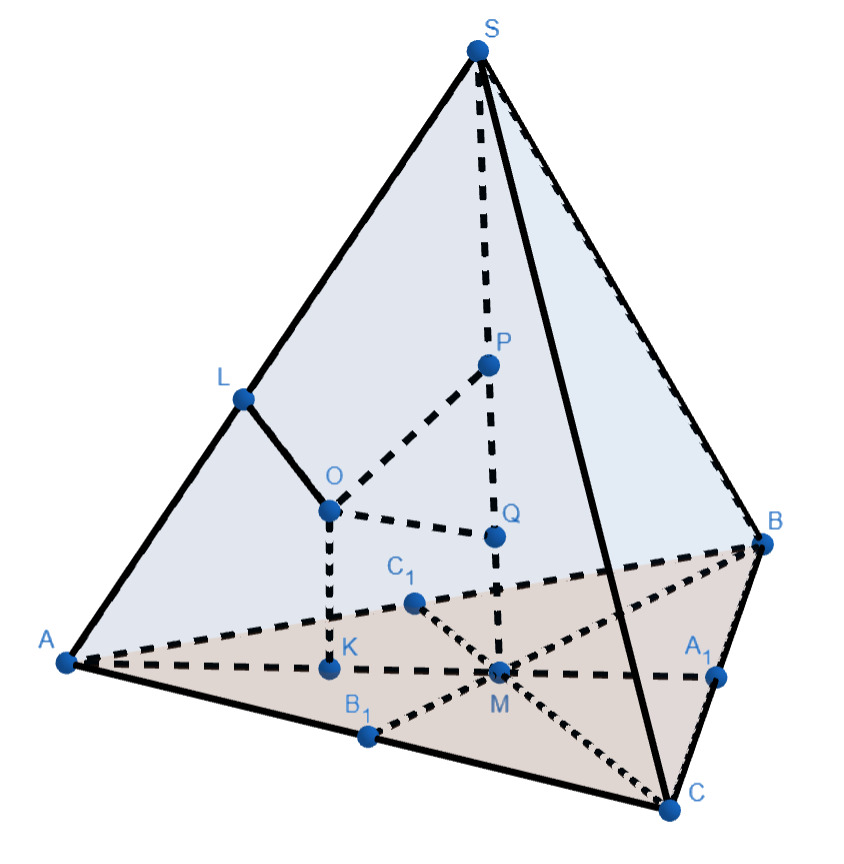
Поскольку — касательная к сфере
а
и
— секущие к ней, то по теореме о касательной и секущей
Аналогично,
А поскольку то
В итоге получаем
Так как как касательные к сфере
проведённые из точки
то
А поскольку медианы треугольника точкой пересечения делятся в отношении считая от вершины, то
Кроме того,
При этом
то есть
Отсюда прямоугольный и
Далее имеем
Значит,
б)
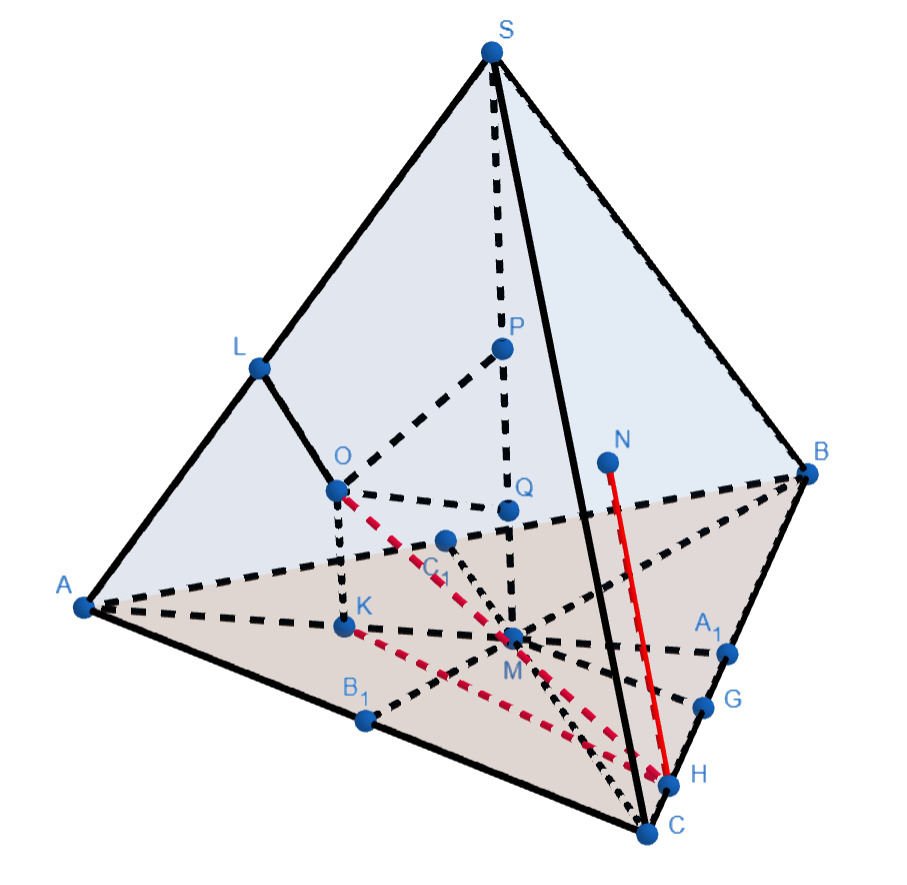
Пусть и
— проекции точек
и
на прямую
соответственно. Заметим, что
потому что
и
— точки касания сферы
со сторонами двугранного угла пирамиды при ребре
Поэтому искомый угол
равен
где — центр сферы
Далее имеем
Так как как касательные к
то
Отсюда получаем
Из подобия и
имеем
Окончательно,
a)
б)
Ошибка.
Попробуйте повторить позже
Дан куб с ребром равным
— сфера, вписанная в каркас этого куба (то есть, касающаяся всех его рёбер). Точка
— середина ребра
Прямая
вторично пересекает сферу
в точке
Найдите
Источники:
Подсказка 1
У нас есть вписанная сфера, а мы хотим найти какой-то отрезок, конец которого лежит на сфере. Может, попробовать применить теорему о касательной и секущей...
Подсказка 2
Наша сфера касается ребра AA₁ в точке K, где K- середина AA₁. Тогда AK²=AX*AM. Надо как-то найти AM...
Подсказка 3
Мы работаем с кубом, поэтому логично было бы поискать теоремки Пифагора. Например для треугольника AMB₁. А почему он прямоугольный?
Подсказка 4
Потому что C₁B₁ перпендикулярен плоскости ABB₁. Тогда по теореме Пифагора для AMB₁: AM²=AB₁²+MB₁². Мы знаем, что B₁M=x/2. Осталось только найти AB₁² и досчитать AX.
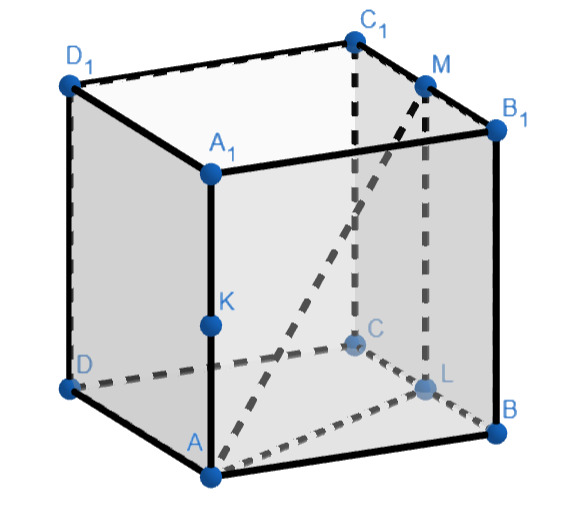
Пусть — середина ребра
тогда
Т.к.
— куб, по теореме Пифагора из прямоугольного
получаем
— середина
а
— середина
следовательно,
как средняя линия квадрата
равна
т.е. равна
Т.к.
— куб, по теореме Пифагора из прямоугольного
получаем
Пусть — середина ребра
тогда
Т.к. сфера
вписана в каркас куба
значит, точками касания
являются середины рёбер. Следовательно, используем теорему о касательной и секущей
Ошибка.
Попробуйте повторить позже
Дана правильная треугольная пирамида. Известно, что центр сферы, описанной около этой пирамиды, равноудалён от боковых рёбер и от
плоскости основания пирамиды. Найдите радиус сферы, вписанной в эту пирамиду, если длина ребра её основания равна
Подсказка 1
Назовём нашу пирамиду SABC, где △ABC будет основанием. Попытаемся узнать длину бокового ребра, пользуясь данными о том, что центр описанной около этой пирамиды сферы равноудалён от боковых рёбер и плоскости основания. Где относительно высоты пирамиды будет расположен центр описанной сферы? Пусть Н — основание высоты, а О₁ — центр описанной сферы. Что можно сказать про △ASH, пользуясь тем, что точка О равноудалена от точки Н и прямой AS, а также от точек S и A?
Подсказка 2
Пирамида правильная, значит мы точно знаем положение точки Н, длину АН и отсюда сможем вытащить AS. Теперь мы знаем длины всех рёбер пирамиды! Подумайте, как можно вытащить радиус вписанной сферы?
Подсказка 3
Центр вписанной сферы О₂ также лежит на высоте пирамиды. Нетрудно доказать, что если М — середина АВ, то именно в плоскости (MSH) будут лежать радиусы, проведённые в точки касания сферы с гранями АВС и SAB. Рассмотрите △MSH, как мы можем в нём посчитать O₂H?
Подсказка 4
MH нетрудно ищется из свойств правильного треугольника. Пифагор поможет нам найти SM и SH. О₂, как точка равноудалённая от сторон МН и MS лежит на биссектрисе угла M. Осталось только применить свойство биссектрисы и задача решена!
Пусть — основание пирамиды,
— вершина,
— центр треугольника
— середина
— центр описанной сферы,
— центр вписанной сферы. Поскольку точка
равноудалена от
и
— биссектриса треугольника
Стало быть,
![]()
Поскольку имеем
откуда
Для треугольника
имеем
откуда
Поскольку
— биссектриса,
Стало быть,
откуда
Ошибка.
Попробуйте повторить позже
Даны четыре точки , не лежащие в одной плоскости. Сфера касается прямых
и
в точке
, а прямых
и
в
точке
Найдите радиус сферы, если известно, что
и углы
и
прямые.
Касательные, проведенные из одной точки к сфере, равны. Значит, и
. Следовательно, треугольники
и
равны по трем сторонам.
Угол прямой, так что высота
треугольника
, опущенная из вершины
, попадает на сторону
Из равенства треугольников
и
следует, что
. Ясно, что плоскость
содержит центр
сферы.
![]()
В прямоугольном треугольнике известны катет
и гипотенуза
Отсюда легко найти, что
.
Из теоремы Пифагора для треугольника
находим, что
(ибо
, а угол
по условию прямой). Кроме
того, из
следует, что
В прямоугольном треугольнике мы нашли катет
и высоту
. Осталась тривиальная планиметрическая задача
нахождения катета
, равного радиусу сферы.
Ошибка.
Попробуйте повторить позже
Сфера касается всех рёбер пирамиды , причём боковых рёбер
и
— в точках
и
Найдите объём пирамиды
, если
и
![]()
Поскольку сфера касается всех рёбер, пирамида обладает тем свойством, что , откуда получаем
, следовательно, треугольник
равносторонний. Тогда треугольник
тоже равносторонний, поэтому
Найдём объём пирамиды как правильной пирамиды с основанием
Поскольку
окончательно получаем
Ошибка.
Попробуйте повторить позже
Сфера касается всех рёбер тетраэдра . Известно, что произведения длин скрещивающихся рёбер равны. Известно также, что
. Найдите
Источники:
Подсказка 1
Подумаем, как можно применить условие о том, что сфера касается всех рёбер тетраэдра? Более всего с длинами рёбер тут связывается свойство касательных: отрезки касательных к сфере, проведенных из одной точки, равны! Обозначьте одной буквой все равные отрезки проведённые из каждой из вершин и при помощи этих букв запишите равенство произведений длин скрещивающихся рёбер. ---
Подсказка 2
Поработайте теперь с нашим двойным равенством: рассмотрите две пары уравнений и попробуйте их преобразовать. Какие интересности связанные с отрезками касательных из разных вершин можно заметить?
Подсказка 3
Если сделать всё аккуратно, то получится несколько вариантов: равны либо отрезки касательных проведённые из вершин А и С, либо проведённые из вершин В и D. Рассмотрите оба случая, не выходит ли в одном из них противоречий с условием задачи? (Не зря же нам даны AB и BC). Аналогично рассмотрите вторую пару вершин, отрезки касательных из которых равны. Останется лишь внимательная арифметика и АС откроется нам!
Расстояния от вершины до точек касания сферы с рёбрами
равны. Обозначим это расстояние
. Соответствующие
расстояния от вершин
обозначим
,
соответственно. По условию
, что
равносильно после раскрытия скобок системе
Если , то
, а это не так. Значит,
. Тогда либо
, либо
. Если
, то
, что
противоречит неравенству треугольника. Значит,
и, стало быть,
Замечание.
Тетраэдр, у которого произведения длин скрещивающихся рёбер равны, называется каркасным, можете поизучать его свойства. В задаче по сути просили доказать, что у такого тетраэдра суммы длин скрещивающихся рёбер равны.
Ошибка.
Попробуйте повторить позже
Около шара радиуса описана правильная
-угольная призма, все ребра которой касаются некоторого другого шара. Докажите, что
и найдите объём этой призмы.
Источники:
Подсказка 1
В этой задаче самое главное — связать боковую сторону и сторону многоугольника основания. Так как в основании у нас правильный многоугольник, в который вписана окружность радиуса 1, то чему в этом случае равна сторона основания? А какой факт можно извлечь из того, что вторая сфера касается каждого ребра?
Подсказка 2
В этом случае, сторона равна 2tg(pi/n) — просто опускаем высоту из центра на какую-нибудь сторону и вычисляем. А вот из того, что вторая сфера касается каждого ребра, следует, что прямоугольник боковой стороны является описанным. Осталось связать этот факт и тот, что в призму вписана сфера с радиусом 1, и получим ответ!
Высота призмы и боковое ребро равны (диаметру вписанного шара). Основания призмы являются правильными
-угольниками,
описанными около окружностей радиуса
Согласно известной формуле, сторона основания в этом случае равна
Поверхность
шара, касающегося рёбер призмы, пересекает каждую из граней по окружности. Это значит, что прямоугольники, служащие боковыми
гранями, описанные, а потому являются квадратами. Отсюда
и
Таким образом, призма представляет собой куб
Ошибка.
Попробуйте повторить позже
(a) Сфера с центром касается боковых рёбер
пирамиды
в точках
соответственно, а
также касается её основания
Через точку сферы, ближайшую к точке
проведена плоскость, касающаяся сферы.
Площадь сечения пирамиды
этой плоскостью равна 9, а
. Найдите площадь треугольника
(b) Пусть дополнительно известно, что а плоскости
и
параллельны. Найдите объём пирамиды
а) Пусть радиус сферы равен . Обозначим точки пересечения прямой
со сферой через
и
(точка
лежит на
отрезке
, а
— вне него). Треугольники
и
прямоугольные (углы при вершинах
прямые,
так как касательные перпендикулярны радиусам, проведённым в точку касания). Эти треугольники равны по катету и
гипотенузе
— общая), следовательно,
(обозначим эти углы через
); высоты, опущенные из точек
на гипотенузу
, равны, а их основания — одна и та же точка
, лежащая в плоскости
(назовём эту плоскость
. Пусть
— касательная плоскость к сфере, проведённая
через точку
. Обозначим точку пересечения
и
через
. Рассмотрим сечение пирамиды и сферы плоскостью
![]()
Из прямоугольного треугольника получаем
. Тогда
Пусть площадь сечения пирамиды плоскостью равна
, а плоскостью
. Из подобия следует, что
Следовательно,
б) Если плоскости и
параллельны, то точка
совпадает с точкой
такой, что
![]()
Тогда, обозначив площадь треугольника через
, получаем
Ошибка.
Попробуйте повторить позже
Сфера радиуса 10 вписана в каркас тетраэдра (т.е. касается всех его рёбер). Сумма длин рёбер тетраэдра составляет 180. Докажите, что объём тетраэдра не превосходит 3000.
Подсказка 1
Во-первых, нам надо понять, через что оценивать. Если у нас есть сфера, которая касается ребер, то это значит, что её сечения гранями - это вписанные в треугольники этих граней окружности. А это значит, что мы можем оценивать объем тетраэдра через маленькие тетраэдры OABC, OABD, OACD, OBCD , где О - центр сферы.
Подсказка 2
Понятно, что ситуация относительно каждого тетраэдра равноправна, потому, нам надо получить оценку только на 1 (то есть, если мы получили какую-то оценку на один маленький тетраэдр, то сможем получить эту же оценку и на другие). Возьмем тогда тетраэдр OABC. Если центр вписанной окружности - это I, то объём OABC равен 1/3 * OI * S(ABC). Как нам тогда связать периметр и объем?
Подсказка 3
Верно, нам надо выразить площадь треугольника как p_abc*r (p_abc - полупериметр). Тогда у нас в силу равнозначности тетраэдров и равнозначности сторон треугольника здесь, при суммировании объемов будет один и тот же коэффициент при каждом ребре тетраэдра и значит, мы выразим площадь. Остается связать r*OI(то, что вылезает при подсчете объема) и R(R - радиус сферы). Как связаны эти три отрезка?
Подсказка 4
Они образуют прямоугольный треугольник. При этом, OI^2 + r^2 = R^2. Значит, у нас есть у нас есть факт, что сумма квадратов OI и r равна квадрату R, а мы хотим оценить произведение. Что нам это должно напомнит?
Подсказка 5
Конечно, неравенство о среднем квадратичном и геометрическом. Тогда, произведение OI*r оценивается сверху как R^2/2. Осталось только сложить все неравенства(ведь мы это проделали только относительно одной грани) и получить требуемое.
Обозначим тетраэдр центр сферы, вписанной в каркас —
а саму сферу —
Объём тетраэдра равен сумме объёмов маленьких
тетраэдров
и
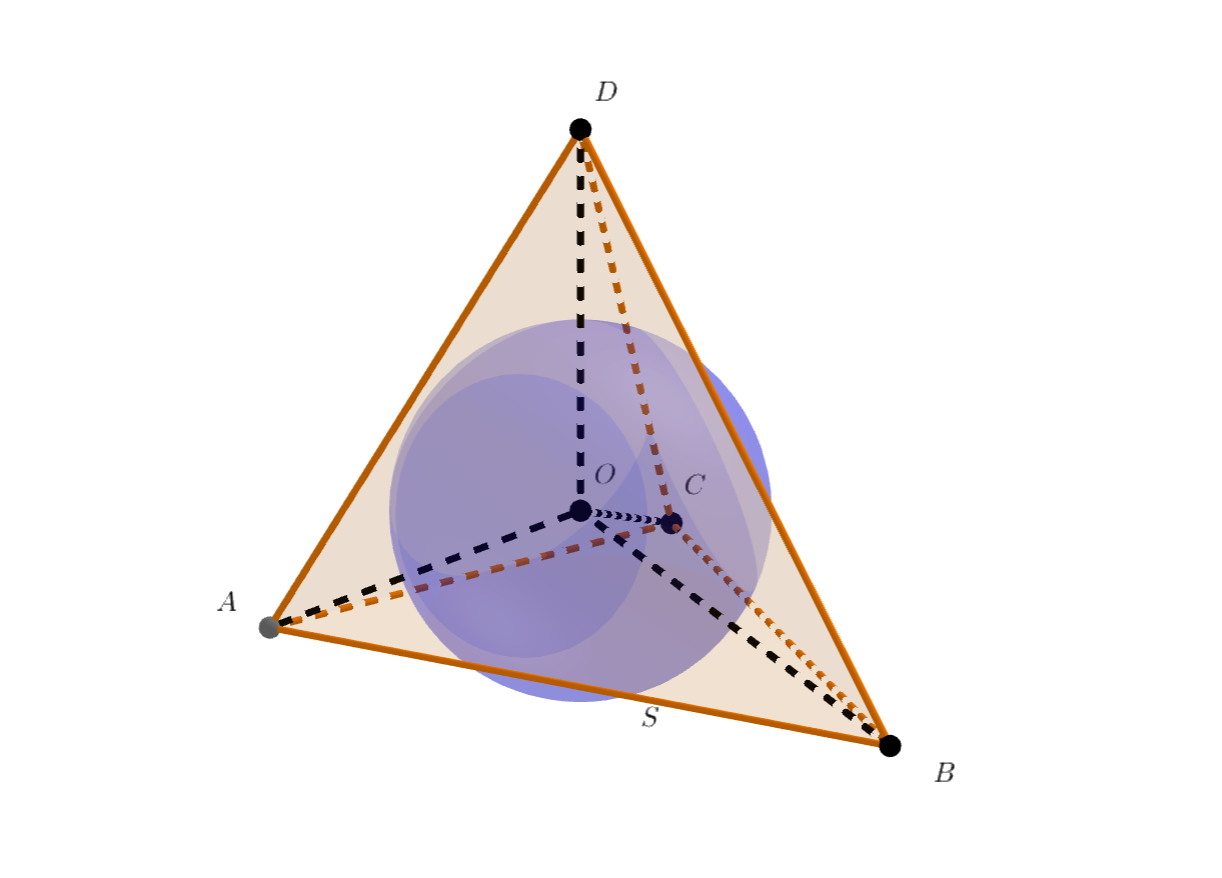
Пересечение и плоскости
это вписанная окружность треугольника
Обозначим за
её центр, тогда
— высота
тетраэдра
Пусть
— радиус сферы
— радиус вписанной окружности треугольника
Тогда выполняется равенство
Тогда
![]()
где — полупериметр треугольника
По неравенству о среднем геометрическом и среднем квадратичном
получаем
то есть
Таким образом,
Складывая объёмы четырёх маленьких тетраэдров, получаем
а сумма полупериметров граней это в точности сумма длин рёбер тетраэдра. Значит,
Ошибка.
Попробуйте повторить позже
В основании треугольной пирамиды лежит прямоугольный треугольник
с гипотенузой
. Сфера
касается
плоскости основания пирамиды и касается всех трёх её боковых рёбер в их серединах. Пусть
— сфера, описанная около пирамиды
(a) Найдите расстояние между центрами сфер и
.
(b) Найдите отношение радиусов сфер и
.
(c) Пусть дополнительно известно, что Найдите объём пирамиды
.
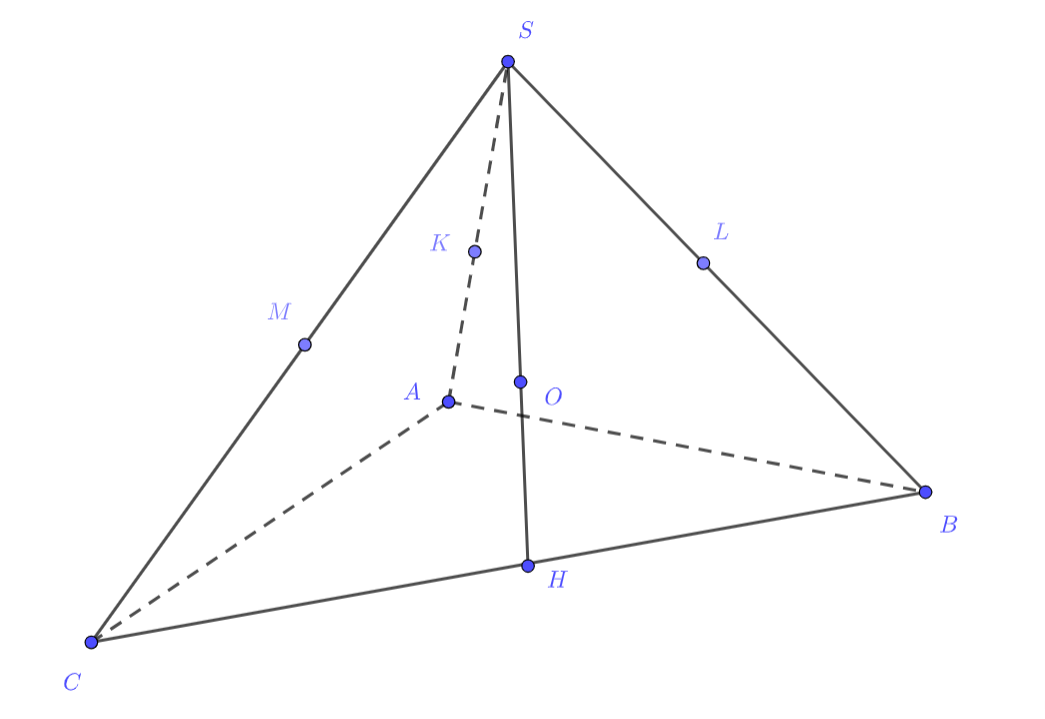
Пусть — центр сферы
— основания перпендикуляров, опущенных из точки
на ребра
соответственно;
—
высота пирамиды
и
— радиусы сфер
и
соответственно.
a) Поскольку точка лежит на серединном перпендикуляре к отрезку
она равноудалена от концов этого отрезка, т.е.
Аналогично
и
Значит,
поэтому точка
является центром сферы
. Следовательно,
расстояние между центрами сфер равно нулю.
b) Из равенства прямоугольных треугольников ,
и
— общая сторона) следует, что
Поскольку точки
— это середины боковых рёбер пирамиды, отсюда получаем, что боковые рёбра
равны между собой. Тогда высота пирамиды проходит через центр окружности, описанной около основания (действительно,
по катету и гипотенузе, откуда
). Но в пирамиде
боковые рёбра
также равны между собой как радиусы сферы
; значит, и её высота, проведённая из вершины
проходит через центр
окружности, описанной около основания. Таким образом, высота пирамиды
проходит через точку
Кроме того, точка
является центром окружности, описанной около основания. Поскольку треугольник
прямоугольный,
—
это середина гипотенузы
Так как отрезок
перпендикулярен плоскости основания, он равен радиусу
сферы
Для нахождения соотношения между радиусами рассмотрим прямоугольный треугольник Точка
— середина гипотенузы
на катете
находится точка
причём
,
Треугольники
,
и
равны по катету
и гипотенузе, следовательно,
Значит,
Тогда из треугольника
находим, что
c) поэтому треугольник
— равносторонний,
B равнобедренном треугольнике
известны боковые стороны
и угол при основании
Отсюда находим, что
.
По теореме Пифагора для треугольника
находим, что
поэтому
объём пирамиды
равен
Ошибка.
Попробуйте повторить позже
Основанием треугольной пирамиды является правильный треугольник
со стороной
Боковое ребро
перпендикулярно основанию и имеет длину
Сфера, центр
которой лежит в плоскости
касается рёбер
,
и
в точках
и
соответственно. Найдите
расстояние от точки
до ребра
и радиус
сферы.
Источники:
Обозначим Пусть
и
проекции точки
на прямые
и
соответственно. Пусть
— радиус сферы.
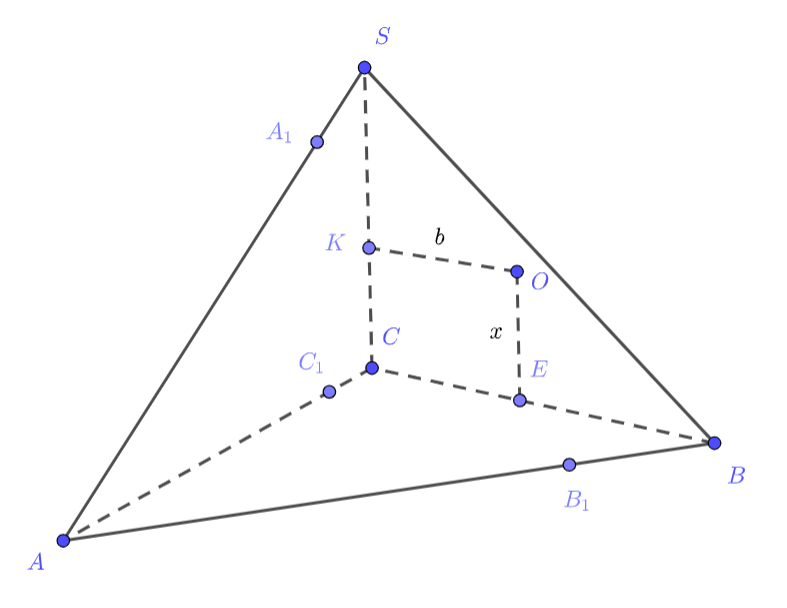
Так как — перпендикуляр к плоскости
, а
то по теореме о трёх перпендикулярах получаем
.
Аналогично
Из равенства прямоугольных треугольников
и
следует, что
Из
равенства прямоугольных треугольников
и
так как
получаем, что
Тогда
Кроме того, из равенств отрезков касательных, проведённых к сфере из точки
следует,
что
Для нахождения
и
выразим
из треугольников
и
Так как
и
то
где
Следовательно,
откуда получаем
T. e. Тогда
.



