Касательные к сфере (+ каркасный тетраэдр)
Ошибка.
Попробуйте повторить позже
Дана треугольная пирамида медианы
и
треугольника
пересекаются в точке
Сфера
касается ребра
в точке
и касается плоскости основания пирамиды в точке
лежащей на отрезке
Сфера
пересекает отрезок
в точках
и
Известно, что
площадь треугольника
равна
а) Найдите произведение длин медиан и
б) Найдите двугранный угол при ребре пирамиды, если дополнительно известно, что
касается грани
в точке
а радиус сферы
равен 5.
Источники:
Пункт а), подсказка 1
Давайте просто начнём хоть что-нибудь делать в задаче и в дальнейшем посмотрим, что из этого получится. У нас есть касание со сферой и секущая. Какой тогда факт связанный со сферой можно сразу заметить?
Пункт а), подсказка 2
Верно, можем записать два выражения по теореме о касательной и секущей. Какую тогда пару равенств отрезков мы получаем?
Пункт а), подсказка 3
Точно, тогда у нас равны произведения в соотношениях, откуда равны SL и MK, а также AM и SA. Но мы знаем, что SA=12 и BC=12. Давайте не будем забывать, что у нас проведены медианы в основании треугольника. Какие тогда ещё отрезки можно найти и какой сделать вывод про треугольник BMC?
Пункт а), подсказка 4
Верно, MA₁=6 по свойству точки пересечения медиан. Но тогда MA₁=BA₁=CA₁=6, и треугольник BMC прямоугольный. Далее, зная площадь треугольника ABC, найти произведение двух оставшихся медиан несложно, так как катеты и будут частями исходных медиан.
Пункт б), подсказка 1
Раз нам нужен двухгранный угол, нужно его сначала построить. Из какой тогда точки удобнее всего опустить перпендикуляр на ребро BC для достижения цели?
Пункт б), подсказка 2
Верно, опустим перпендикуляр KH из точки K. Но тогда, применяя несколько раз теорему о трёх перпендикулярах, получаем, что NH ⊥ BC. Значит нам нужно искать ∠NHK. Но из-за равенства двух прямоугольных треугольников, ∠NHK = 2∠OHK, где O — центр сферы. Чтобы найти угол, скорее всего, надо будет найти сторону прямоугольного треугольника. Но её мы пока не знаем... Какой дополнительное построение тогда можно сделать, где нам что-то известно?
Пункт б), подсказка 3
Верно, давайте проведём ещё высоту в треугольнике BMC, которую мы можем найти. А также у нас два треугольника подобны. Осталось только до конца воспользоваться равенством касательных к сфере, после чего найти неизвестный катет, и, следовательно, двухгранный угол.
а)
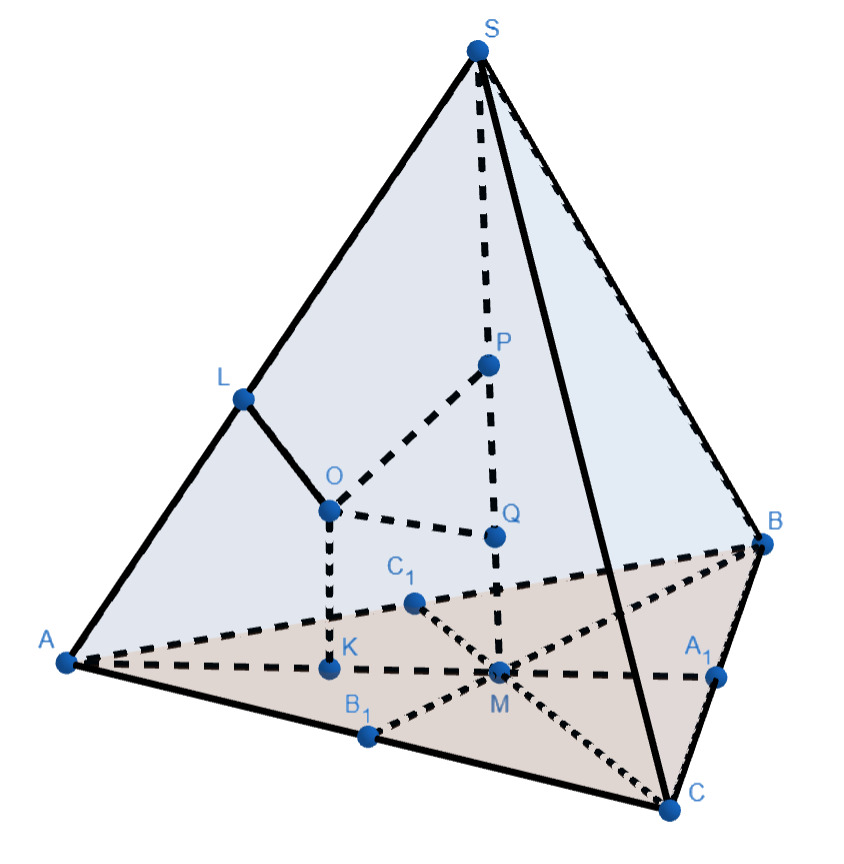
Поскольку — касательная к сфере
а
и
— секущие к ней, то по теореме о касательной и секущей
Аналогично,
А поскольку то
В итоге получаем
Так как как касательные к сфере
проведённые из точки
то
А поскольку медианы треугольника точкой пересечения делятся в отношении считая от вершины, то
Кроме того,
При этом
то есть
Отсюда прямоугольный и
Далее имеем
Значит,
б)
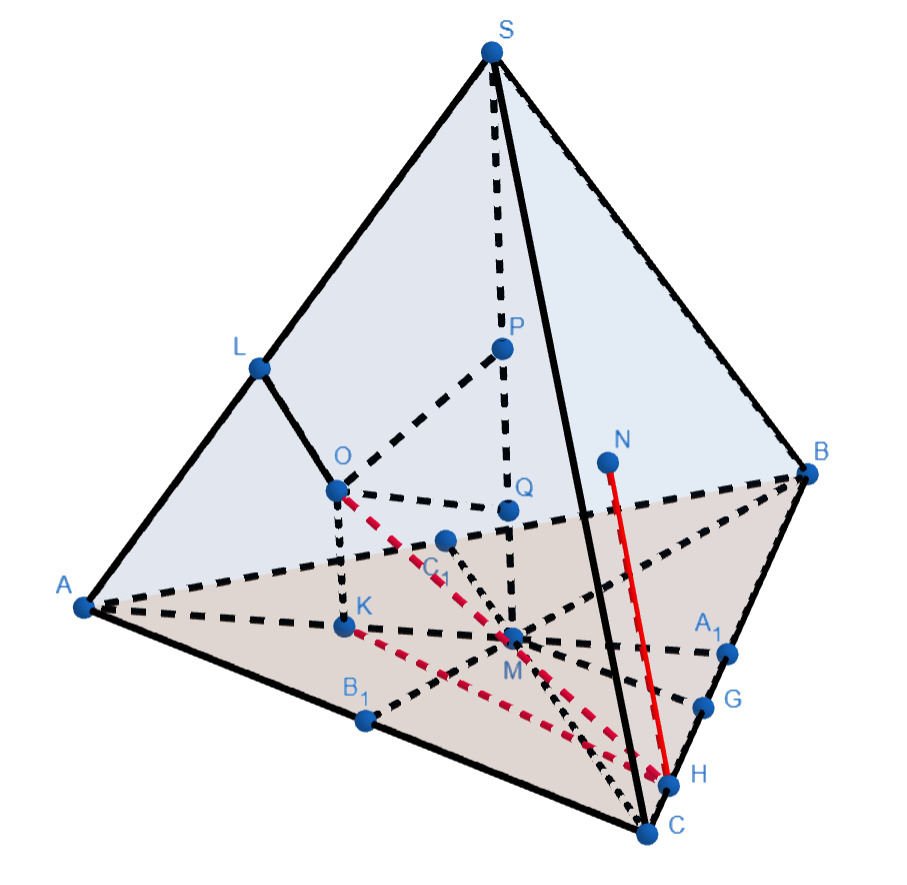
Пусть и
— проекции точек
и
на прямую
соответственно. Заметим, что
потому что
и
— точки касания сферы
со сторонами двугранного угла пирамиды при ребре
Поэтому искомый угол
равен
где — центр сферы
Далее имеем
Так как как касательные к
то
Отсюда получаем
Из подобия и
имеем
Окончательно,
a)
б)
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




