Касательные к сфере (+ каркасный тетраэдр)
Ошибка.
Попробуйте повторить позже
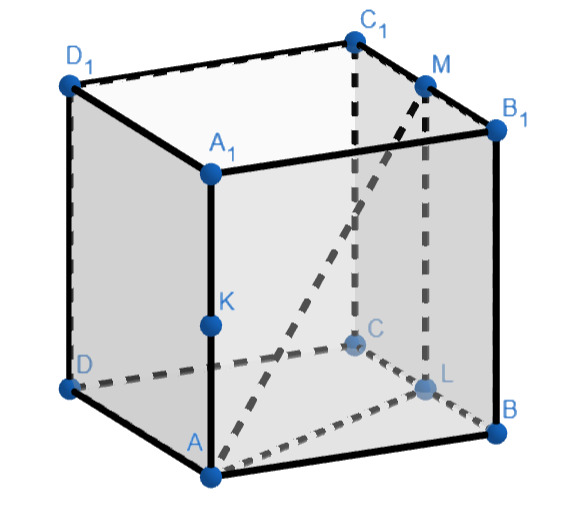
Дан куб с ребром равным
— сфера, вписанная в каркас этого куба (то есть, касающаяся всех его рёбер). Точка
— середина ребра
Прямая
вторично пересекает сферу
в точке
Найдите
Источники:
Подсказка 1
У нас есть вписанная сфера, а мы хотим найти какой-то отрезок, конец которого лежит на сфере. Может, попробовать применить теорему о касательной и секущей...
Подсказка 2
Наша сфера касается ребра AA₁ в точке K, где K- середина AA₁. Тогда AK²=AX*AM. Надо как-то найти AM...
Подсказка 3
Мы работаем с кубом, поэтому логично было бы поискать теоремки Пифагора. Например для треугольника AMB₁. А почему он прямоугольный?
Подсказка 4
Потому что C₁B₁ перпендикулярен плоскости ABB₁. Тогда по теореме Пифагора для AMB₁: AM²=AB₁²+MB₁². Мы знаем, что B₁M=x/2. Осталось только найти AB₁² и досчитать AX.
Пусть — середина ребра
тогда
Т.к.
— куб, по теореме Пифагора из прямоугольного
получаем
— середина
а
— середина
следовательно,
как средняя линия квадрата
равна
т.е. равна
Т.к.
— куб, по теореме Пифагора из прямоугольного
получаем
Пусть — середина ребра
тогда
Т.к. сфера
вписана в каркас куба
значит, точками касания
являются середины рёбер. Следовательно, используем теорему о касательной и секущей
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




