Счёт в синусах и просто теорема синусов
Ошибка.
Попробуйте повторить позже
Пусть — ортоцентр остроугольного треугольника
. Докажите, что
Подсказка 1
Тригонометрия в соотношении, которое нам нужно доказать, и куча прямых углов —> счёт в синусах явно может нам помочь! Отыщите прямоугольные треугольники, в которых фигурируют все 3 объекта из равенства в условии, и поработайте с ними!
Подсказка 2
Попробуйте от одной стороны, домножая на синусы/косинусы, пропутешествовать к другой! Например, домножив (или разделив?) BC на синус угла BCA, мы превратим его в высоту из вершины B. А эту же высоту мы можем превратить с помощью угла BAC (а он нам нужен!) в AB₁ Как теперь от AB₁ добраться до AH? Не забывайте: куча прямых углов —> куча вписанных четырёхугольников —> куча равных углов
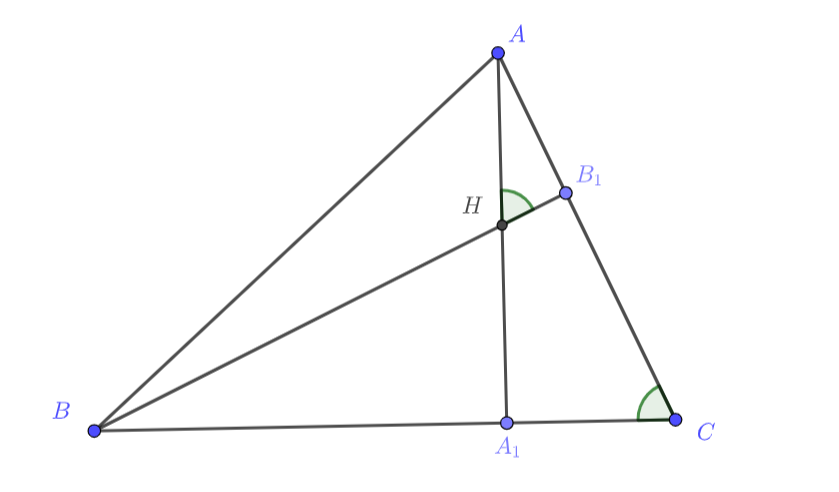
Обозначим основания высот из точек и
за
и
соответственно. Из прямоугольного
имеем
Тогда из прямоугольного получаем
Остаётся заметить, что вписанный, так как
, поэтому
. Значит, из
выполнено
Замечание. Подумайте, как поправить формулу расстояния от вершины до ортоцентра, чтобы она была корректной не только в случае остроугольного треугольника.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




