Счёт в синусах и просто теорема синусов
Ошибка.
Попробуйте повторить позже
На биссектрисе угла с вершиной отмечена точка
. Через
проводится прямая, пересекающая стороны угла в точках
и
.
Докажите, что величина
не зависит от выбора прямой.
Подсказка 1
Какая-то величина не зависит от выбора прямой —> пробуем выразить её через что-то фиксированное на рисунке! А у нас в целом на рисунке не так много всего, так что попробуйте эти фиксированные объекты для начала найти, а затем подумать, как бы их связать с величиной из условия
Подсказка 2
Например, у нас есть фиксированные углы, на которые биссектриса делит угол А, и длина АР. Угол и сторона —> может, поможет теорема синусов? И в ней как раз есть дроби, как в нашем соотношении из условия! Можем записать по теореме синусов на треугольник, выразить из них 1/AB и 1/AC, а дальше дело техники (тригонометрической)!
Первое решение.
Покажем, что сумма из условия выражается через инвариантные относительно выбора точек и
параметры
и
При произвольном выборе
для треугольника
по теореме синусов получаем
А для треугольника по теореме синусов
Складывая эти равенства, получаем
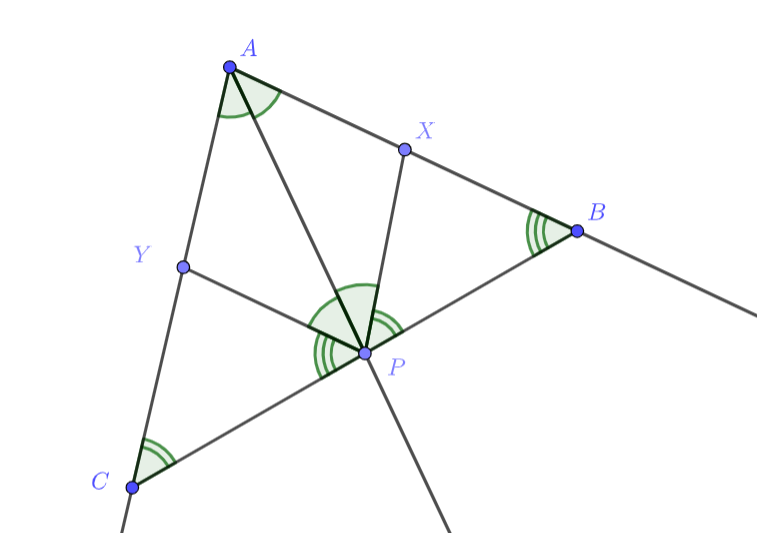
Второе решение.
Выберем на
и
так, что
и
. Отметим равные углы (помним, что
— биссектриса), откуда в
параллелограмме
все стороны равны и
. Заметим, что
, откуда выполнено
Поскольку не зависит от выбора прямой по построению, то требуемое доказано.
что и требовалось доказать
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




