Счёт в синусах и просто теорема синусов
Ошибка.
Попробуйте повторить позже
Пусть — высоты остроугольного треугольника
. Докажите, что треугольник с вершинами в ортоцентрах
треугольников
,
равен треугольнику
.
Подсказка 1
Конструкция громоздкая! Если нарисовать треугольник с вершинами в ортоцентрах, то увидеть что-то будет проблемно. Так как тогда стоит переформулировать условие? Если мы хотим доказать, что треугольники равны, то явно не с помощью углов – углы треугольника с вершинами в ортоцентрах неудобно “летают в воздухе”. Тогда можно доказать равенство трёх сторон! При аккуратном построении картинки можно даже догадаться каких, а учитывая некую симметрию в нашей картинки при поворотах треугольника, можно в целом сказать, что мы лишь хотим равенства двух отрезков!
Подсказка 2
Проведите те самые отрезки, равенство которых мы хотим – если мы знаем, что они равны, то образуется приятный параллелограммчик. Параллельность двух других сторон в нём мы и так знаем, а значит остаётся доказать их равенство – и вот они уже не выглядят “висящими в воздухе”! Так, мы что-то много думали – пора считать! Как это и бывает часто полезно, введём все углы искомого треугольника и радиус его описанной окружности – через них и посчитаем искомые два отрезка
Подсказка 3
Попробуем каждый из этих отрезков “перенести” на части сторон искомого треугольника: свяжите их с помощью теоремы синусов в треугольниках, где они лежат вместе! Это и поможет нам выразить всё через введённые переменные! Ведь теперь нам нужно лишь перенести углы из этого треугольника в более удобное место (куча вписанностей поможет) + выразить отрезок на стороне треугольника (а это мы легко умеем!), и задача будет убита
Кстати, искомые отрезки – это расстояния от вершин до ортоцентра в соответствующих треугольниках, а такие расстояния связаны изящно с противоположной стороной через котангенс угла. Можно с помощью этой связи раскрутить счёт побыстрее!)
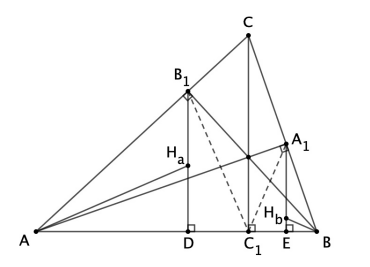
Пусть — ортоцентры треугольников
,
соответственно. Докажем равенство
, откуда
аналогично последуют равенства
и
, поскольку все обозначения в задаче симметричны, и искомые
треугольники окажутся равны по трём сторонам.
Прямые и
перпендикулярны
, поэтому
. Докажем, что
, откуда последует, что
параллелограмм, и
окажется равен
.
Вычислим отрезок . Пусть
.
— радиус описанной окружности треугольника
.
Поскольку четырёхугольник
вписан (
— диаметр, на который опираются равные углы по
), то
и
. Аналогично
.
Первое решение.
В остроугольном треугольнике расстояние от вершины до ортоцентра равно произведению котангенса угла при этой вершине на длину
противоположной стороны. То есть По тем же причинам
Второе решение.
Поскольку и
, то
и
. По теореме синусов в треугольнике
имеем
Поскольку это выражение симметрично относительно и
, то и отрезок
равен тому же (
станет им, если поменять
вершины
и
местами).
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




