Счёт в синусах и просто теорема синусов
Ошибка.
Попробуйте повторить позже
Дан угол, равный . На его биссектрисе взята точка
;
и
— проекции
на стороны угла. На отрезке
взята точка
,
причём
. Прямая, проходящая через
перпендикулярно
, пересекает стороны угла в точках
и
. Найдите площадь
треугольника
.
Подсказка 1!
1) У нас в задаче опять обилие прямых углов! Знак того, что можно поискать вписаности!
Подсказка 2!
2) Верно, рассмотрим четырехугольники BAKP и KAMC. В них по два прямых угла, а это значит, что они вписанные, и можно написать несколько равенств углов. Хм, кажется, что у нас на картинке есть еще один приятный четырехугольник XPKM. Попробуем использовать свойства всех этих четырехугольников!
Подсказка 3!
3) Ага, нам нужно получить равенство углов BKA и CKA, а дальше площадь треугольника BCK вычислится сама собой, ведь мы знаем биссектрису (хм, только ли биссектрису...) и угол!
Точка лежит на биссектрисе угла
, поэтому ясно, что
и
— вписанный
дельтоид,
Рассмотрим два случая выбора точки на отрезке
:
. Тогда
. Тогда
В случае
рассуждение совпадает с точностью до переобозначений.
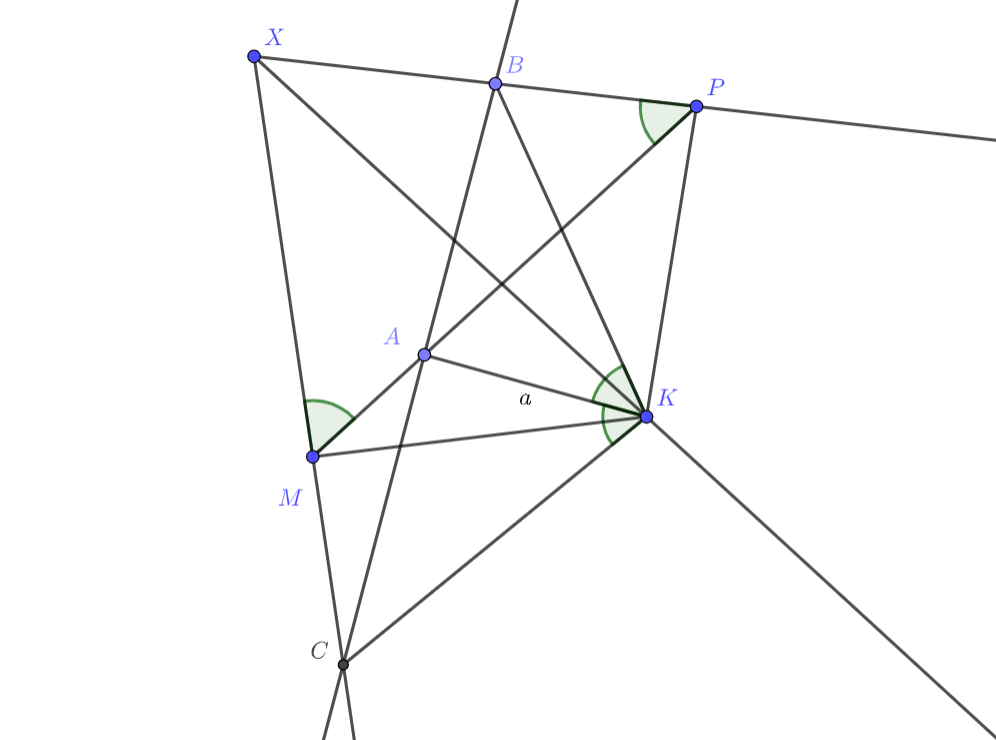
Заметим, что вписан, поскольку
, отсюда
.
Аналогично из получаем вписанность
и равенство
.
Итак, является биссектрисой и высотой
, откуда он равнобедренный, его площадь
.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




