Счёт в синусах и просто теорема синусов
Ошибка.
Попробуйте повторить позже
Дан треугольник, у которого длины сторон — числа рациональные. Докажите, что рациональным числом является
а) отношение где
и
— радиусы описанной и вписанной
окружности;
б) значение где
— углы треугольника.
Источники:
Пункт а), подсказка 1
В условии сказано сразу про три стороны треугольника. Какие формулы сразу с величинами всех сторон есть в геометрии?
Пункт а), подсказка 2
Если в условие что-то говорится сразу про три стороны треугольника, то полезным будет воспользоваться формулами площади для треугольника: через стороны и радиус описанной, через полупериметр и радиус вписанной и формулой Герона.
Пункт а), подсказка 3
Правильно выразив и подставив величины из формул, можно найти отношение R/r.
Пункт б), подсказка 1
Полезным будет выразить гамма через альфа и бетта, пользуясь теоремой о сумме углов треугольника.
Пункт б), подсказка 2
Вместо гамма теперь в аргументе синуса стоит (180-альфа-бетта) Нужно попробовать свести все аргументы к сумме либо разности альфа и бетта.
Пункт б), подсказка 3
Аккуратно и правильно примените несколько тригонометрических формул из произведения в сумму.
Пункт б), подсказка 4
В конечном итоге мы получаем выражение которое зависит только от косинусов альфа, бетта и гамма. Рациональность данных величин нетрудно доказать, используя теорему косинусов.
Первое решение.
Введём длины сторон, как
— площадь,
— полупериметр. Далее воспользуемся формулами
откуда
Для углов известно зная это, распишем произведение
Осталось воспользоваться теоремой косинусов. Например, для угла имеем
То есть косинусы также рациональны, откуда следует рациональность произведения.
Второе решение.
а)
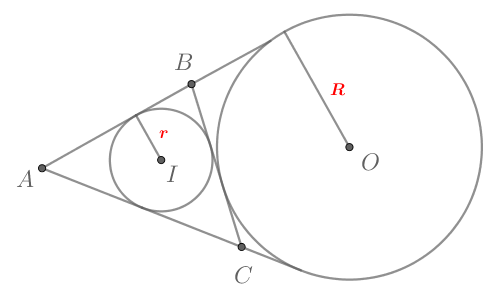
Мы знаем, что где
— площадь треугольника, а
— его полупериметр. С другой стороны,
где
—
стороны треугольника. Тогда
Следовательно,
По формуле Герона
Тогда
Заметим, что здесь каждый из множителей рационален, а следовательно и отношение рационально.
б) Запишем теорему синусов:
Отсюда получаем
Пусть — точка пересечения биссектрис треугольника
Рассмотрим треугольник
и запишем для него теорему
синусов:
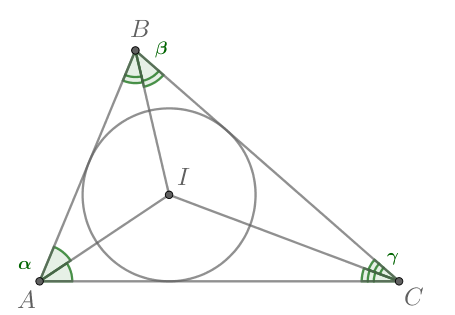
Подставим распишем синус двойного угла и синус суммы, получим
Отсюда получаем
Аналогично
Заметим, что
Таким образом,
Тогда
По предыдущему пункту рационально, значит и
рационально.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




