Счёт в синусах и просто теорема синусов
Ошибка.
Попробуйте повторить позже
В неравнобедренном треугольнике серединные перпендикуляры к сторонам
и
пересекают высоту из вершины
в точках
и
соответственно. Найдите радиус описанной около этого треугольника окружности, если
Источники:
Пусть для определенности углы — острые, обозначим
. Так как
— высота, то
Пусть
— середины
соответственно.
Первое решение.
![]()
Отметим точку пересечения серединных перпендикуляров
и
к сторонам треугольника
. Эта точка является центром
описанной около треугольника окружности. Заметим, что угол
вдвое меньше центрального угла
поэтому равен
вписанному углу
то есть
При этом
из вписанности четырёхугольника
(два прямых угла
дают вписанность). Тогда обратим внимание, что
касается описанной окружности треугольника
, так как угол
между ней и хордой
равен углу
опирающемуся на эту хорду. По теореме о касательной и секущей получаем
Второе решение.
![]()
Не будем думать и посчитаем в синусах: из прямоугольных треугольников
Тогда получается
Наконец, по теореме синусов радиус описанной окружности равен
Ошибка.
Попробуйте повторить позже
Две окружности радиусов и
касаются прямой
в точках
и
. Пусть
— точка пересечения этих окружностей,
наиболее удалённая от
. Докажите, что радиус описанной окружности треугольника
не зависит от положения
окружностей.
Не нарушая общности, точка принадлежит окружности радиуса
назовём её
а точка
принадлежит окружности радиуса
назовём её

Пусть
Тогда на дугу
в
опирается вписанный
угол
поэтому
аналогично
По теореме синусов имеем
что не зависит от положения окружностей.
Ошибка.
Попробуйте повторить позже
Окружности радиусов и
касаются внутренним образом в точке
. Хорда
большей окружности перпендикулярна
диаметру
меньшей окружности.
— одна из точек пересечения
с меньшей окружностью. Найти радиус окружности, описанной
около треугольника
.
Обозначим центры окружностей как и
соответственно.
Тогда .
![]()
Треугольники и
равнобедренные, пусть
и
Тогда по свойству внешнего угла треугольника
По теореме синусов в треугольнике получаем
По теореме синусов в треугольнике получаем
Теперь применим теорему синусов к треугольнику обозначив искомый радиус описанной около него окружности за
Следовательно
Ошибка.
Попробуйте повторить позже
В остроугольном треугольнике отметили основания высот
из вершин
и
соответственно. Пусть
—
окружности, вписанные в треугольники
и
соответственно, касающиеся сторон
и
в точках
и
соответственно. Пусть прямая
вторично пересекает окружности
в точках
и
соответственно. Докажите, что
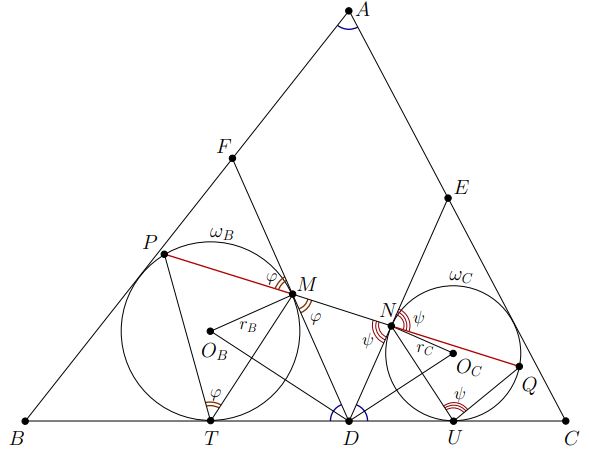
Пусть и
— центры
и
их радиусы —
и
а точки касания с
—
и
Из вписанных четырёхугольников
и
имеем:
Значит, прямоугольные треугольники и
подобны c коэффициентом
Пусть и
Прямые
и
касаются
и
откуда:
(Возможно, что точка или
совпала с
или
или лежит внутри треугольника
или
Чтобы убрать привязку к
конкретным случаям, можно использовать направленные углы)
В окружностях и
длины хорд
и
равны соответственно:
Напишем теорему синусов для треугольника
Наконец, собирая все полученные равенства:
получаем требуемое.
Ошибка.
Попробуйте повторить позже
В окружность вписан четырёхугольник
. На стороне
отмечена точка
таким образом, что
и
. Найдите радиус окружности
, если известно, что
и
.
Источники:
Первое решение.
![]()
из треугольника
из треугольника
из вписанности четырёхугольника
По теореме синусов для треугольника
По теореме синусов для треугольника
Наконец, применяя теорему синусов для :
Подставляем в последнюю пропорцию выражения для и
, которые получили выше:
Отсюда видно, что подходит, т.к.
, а из
понятно, что этот угол определяется однозначно (он лежит в интервале от до
, и мы знаем численное значение его
котангенса).
Таким образом, можно выразить радиус окружности из треугольника
______________________________________________________________________________________________________________________________________________________
Второе решение.
Посчитаем углы:
Отметим на такую точку
что
![]()
Тогда то есть
откуда
А
то есть
откуда
Значит, треугольник
равнобедренный, а так как
то
ещё и равносторонний, то есть
Итак, мы получили, что
откуда точка является центром окружности, описанной около треугольника
Отсюда искомый радиус равен
1.
Ошибка.
Попробуйте повторить позже
Внутри угла с вершиной отмечена точка
Рассматриваются всевозможные
пары точек
и
на сторонах угла такие, что
Докажите, что
все прямые
пересекаются в одной точке.
Проведём через точку прямую, перпендикулярную
Пусть она пересекает
стороны угла в точках
и
причем точки
и
лежат на одной стороне
угла, точки
и
— на другой.
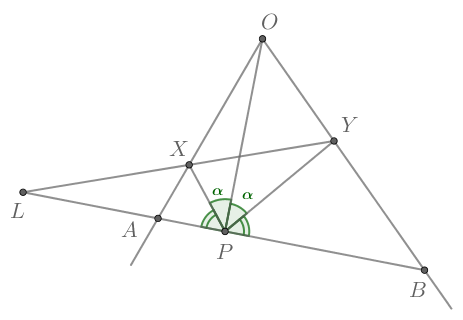
Обозначим за
По условию
Тогда
Рассмотрим треугольник По теореме синусов
В треугольнике по теореме синусов
Сумма смежных углов равна поэтому
Тогда
Тогда
Аналогично запишем отношение
Пусть По теореме Менелая для треугольника
Так как расположение точек и
не зависит от выбора точек
и
то отношение
фиксированно и зависит только от выбора точки
Тогда и отношение
фиксированно и не зависит от выбора точек
и
а значит, все прямые
пересекают
в точке
для
которой верно
Тогда все прямые
пересекаются в одной
точке.
Ошибка.
Попробуйте повторить позже
Дан треугольник, у которого длины сторон — числа рациональные. Докажите, что рациональным числом является
а) отношение где
и
— радиусы описанной и вписанной
окружности;
б) значение где
— углы треугольника.
Источники:
Первое решение.
Введём длины сторон, как
— площадь,
— полупериметр. Далее воспользуемся формулами
откуда
Для углов известно зная это, распишем произведение
Осталось воспользоваться теоремой косинусов. Например, для угла имеем
То есть косинусы также рациональны, откуда следует рациональность произведения.
Второе решение.
а)
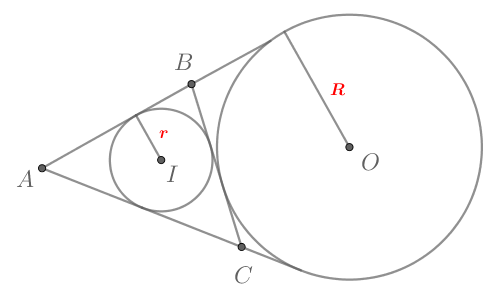
Мы знаем, что где
— площадь треугольника, а
— его полупериметр. С другой стороны,
где
—
стороны треугольника. Тогда
Следовательно,
По формуле Герона
Тогда
Заметим, что здесь каждый из множителей рационален, а следовательно и отношение рационально.
б) Запишем теорему синусов:
Отсюда получаем
Пусть — точка пересечения биссектрис треугольника
Рассмотрим треугольник
и запишем для него теорему
синусов:
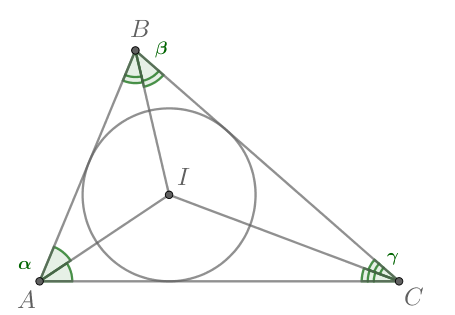
Подставим распишем синус двойного угла и синус суммы, получим
Отсюда получаем
Аналогично
Заметим, что
Таким образом,
Тогда
По предыдущему пункту рационально, значит и
рационально.
Ошибка.
Попробуйте повторить позже
B неравнобедренном треугольнике проведены биссектрисы
и
. Известно, что
и что радиус
окружности, касающейся стороны
и продолжений сторон
и
, равен 1. Найдите периметр треугольника
Источники:
![]()
Докажем, что . Для этого положим
,
и воспользуемся теоремой синусов.
Имеем:
откуда
С учетом условия это означает, что
. Равенству
противоречит условие
задачи.
Поэтому , откуда
и
Теперь найдем периметр треугольника . Пусть окружность с центром
касается стороны
в точке
, а продолжений
сторон
и
- в точках
и
соответственно.
Тогда и
Ошибка.
Попробуйте повторить позже
В треугольнике с тупым углом проведены высоты
и
Докажите, что отрезок, соединяющий проекции точки
на прямые
и
, равен отрезку, соединяющему проекции точки
на прямые
и
Пусть проекции на
это
, проекции
на
—
. Тогда требуется показать
Пусть ,
. Тогда
.
Заметим, что вписан в окружность с диаметром
, поскольку в нём
. Отсюда по теореме
синусов
Далее можно сразу заметить симметричность обозначений, а можно повторить рассуждения для и вписанного
.
Ошибка.
Попробуйте повторить позже
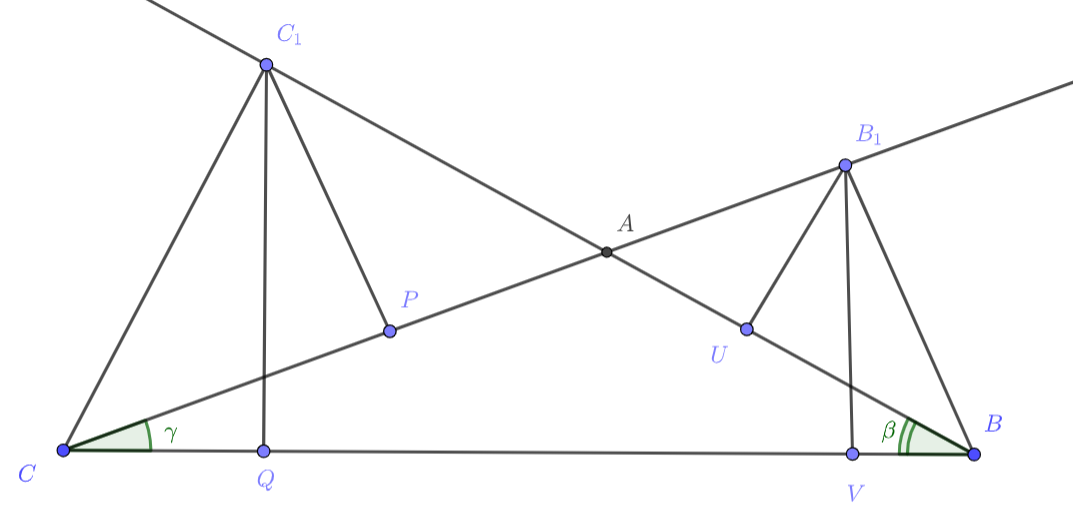
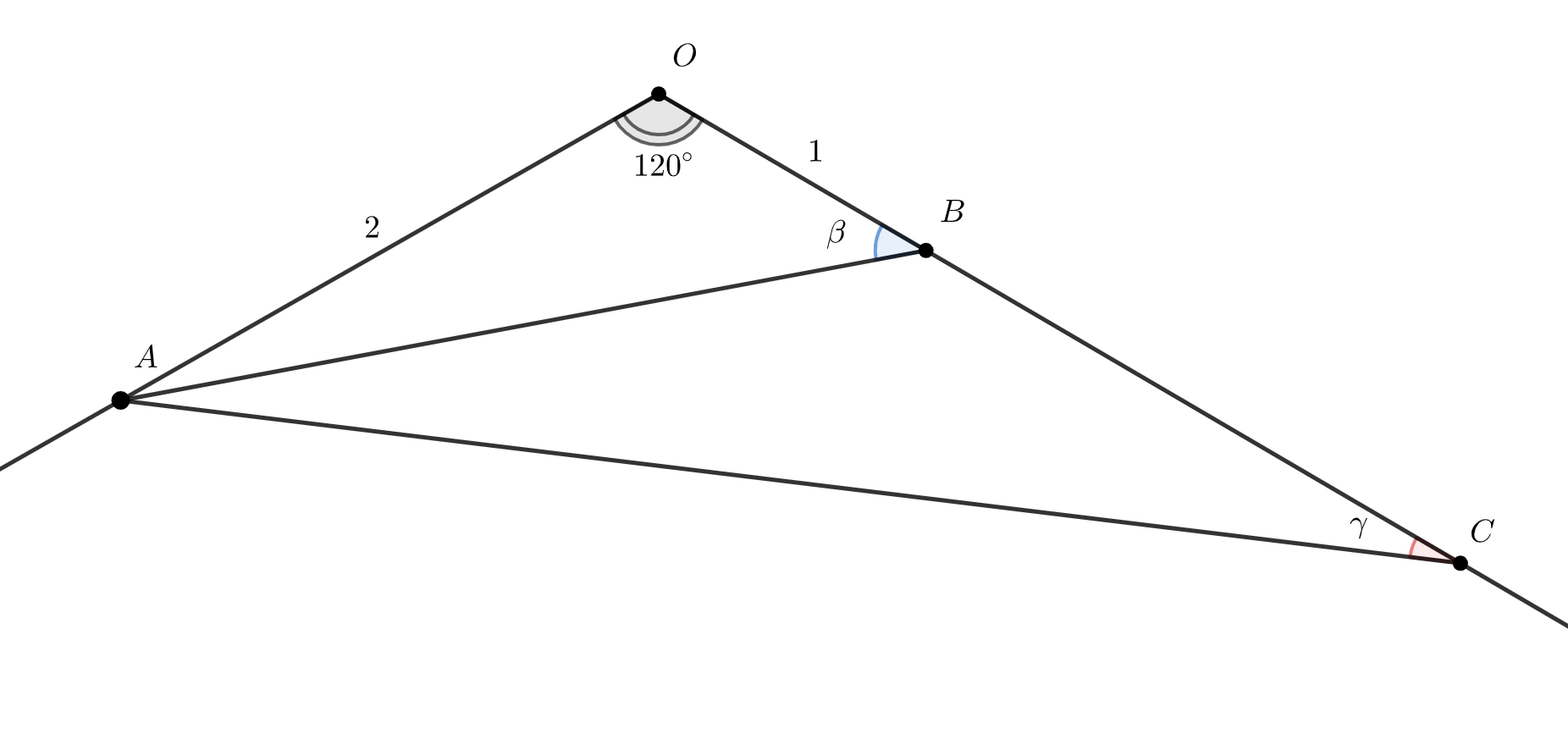
Дан угол с вершиной в точке и градусной мерой
. На одной его стороне отмечена точка
, на другой — точки
и
.
Известно, что
,
. Оказалось, что тангенс угла
в два раза больше тангенса угла
. Найдите
.
Источники:
Обозначим угол через
, угол
— через
.
Из теоремы синусов для треугольника имеем
, откуда
. Поделив на
и
применив формулу синуса разности, получаем
. Аналогично
. Вспомнив, что
, получаем уравнение
Ошибка.
Попробуйте повторить позже
Выпуклый шестиугольник вписан в окружность. Докажите, что его диагонали
,
,
пересекаются в одной точке
тогда и только тогда, когда
Предположим, что диагонали шестиугольника пересекаются в одной точке. Рассмотрим треугольник В нем прямые
и
являются чевианами, пересекающимися в одной точке.
Тогда, согласно синусной теореме Чевы
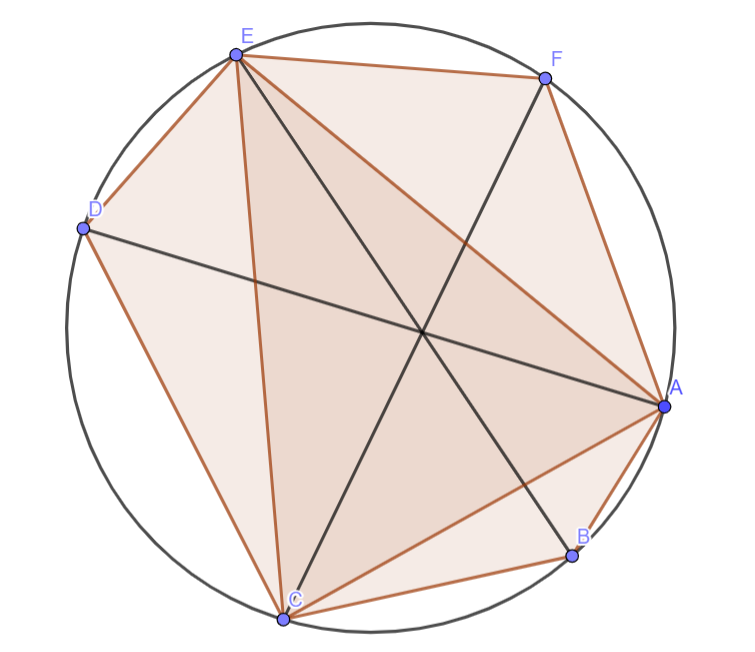
Из теоремы синусов следует, что синусы двух углов в окружности относятся также, как и хорды, на которые они опираются. Заменим в выражении выше отношения синусов на отношения хорд:
что и требовалось доказать.
В обратную сторону утверждение доказывается с помощью обратной синусной теоремы Чевы. Снова выделим треугольник По
условию
и значит
Согласно теореме, чевианы
и
пересекаются в
одной точке.
Ошибка.
Попробуйте повторить позже
Биссектриса угла треугольника
пересекает
в точке
Через середину
провели прямую, пересекающую стороны
и
в точках
и
Докажите, что
Докажем для начала следующую лемму.
Лемма. — треугольник,
— чевиана в нём. Тогда
Доказательство. Запишем теорему синусов для треугольников и
Теперь мы можем выразить отсюда и
Подставим в наше равенство
Так как синусы смежных углов равны, то можем вынести общий множитель, а сумма отрезков станет равна Перепишем равенство
в таком виде
Заменим левую часть по теореме синусов для треугольника
Теперь мы можем сократить на тем самым получая на самом деле теорему синусов для треугольника
Лемма
доказана.
_________________________________________________________________________________________________________________________________________________________________________________
Пусть – середина
Применим лемму к треугольнику
и чевиане
а также к треугольнику
и чевиане
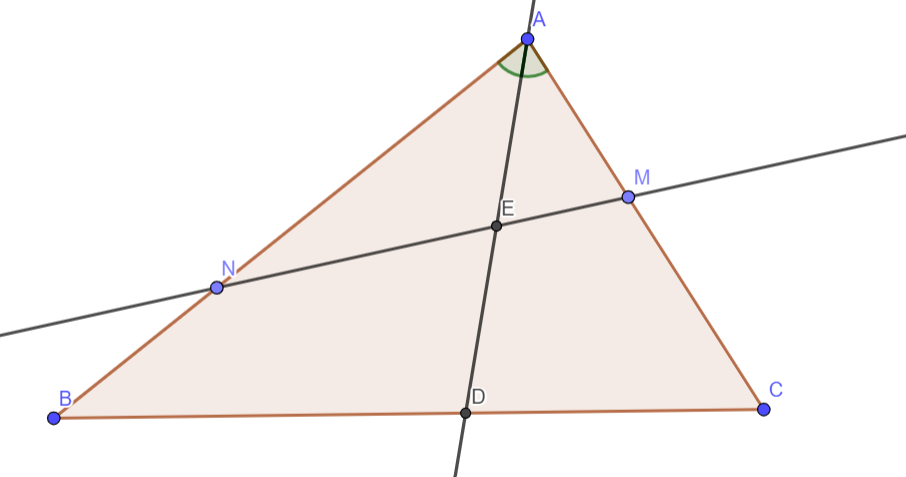
Левая часть второго тождества вдвое большое левой части первого. Запишем, что правая часть второго тождества также вдвое больше правой части первого
Чтобы получить утверждение задачи, осталось поделить обе части на
Ошибка.
Попробуйте повторить позже
Точка — центр описанной окружности треугольника
Прямая
пересекает
в точке
Точки
и
на сторонах
и
соответственно таковы, что
и
лежат на одной окружности. Докажите, что длина проекции отрезка
на прямую
не зависит от положения точек
и
Пусть Тогда, по теореме синусов
Аналогично,
Из треугольника
угол между прямыми
и
составляет
поэтому проекция
на
равна
по формуле косинуса суммы.
Аналогично, из треугольника можно найти угол между прямыми
и
и вычислить длину проекции
на
Ясно, что длина проекции на
равняется сумме длин проекций
и
на
Нетрудно видеть, что первые слагаемые в
выражениях длин проекций
и
сокращаются при сложении, и остается сумма
и это выражение зависит от элементов треугольника но не зависит от выбора точек
и
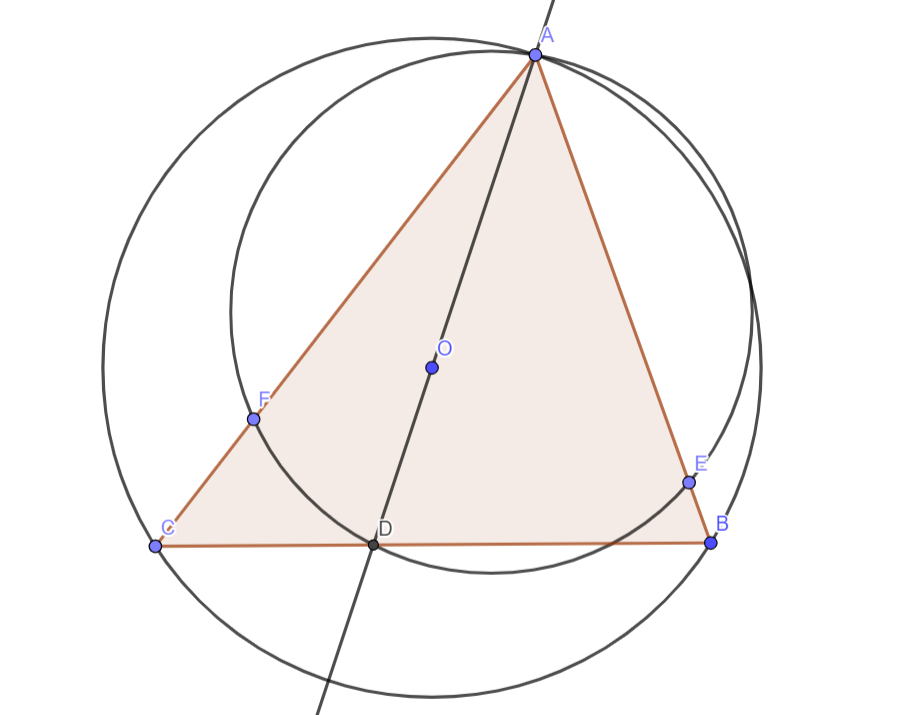
Ошибка.
Попробуйте повторить позже
Пусть — окружность, описанная около остроугольного треугольника
Точки
и
лежат на отрезках
и
соответственно, причём
Серединные перпендикуляры к отрезкам
и
пересекают меньшие дуги
и
окружности
в точках
и
соответственно. Докажите, что прямые
и
параллельны, или
совпадают.
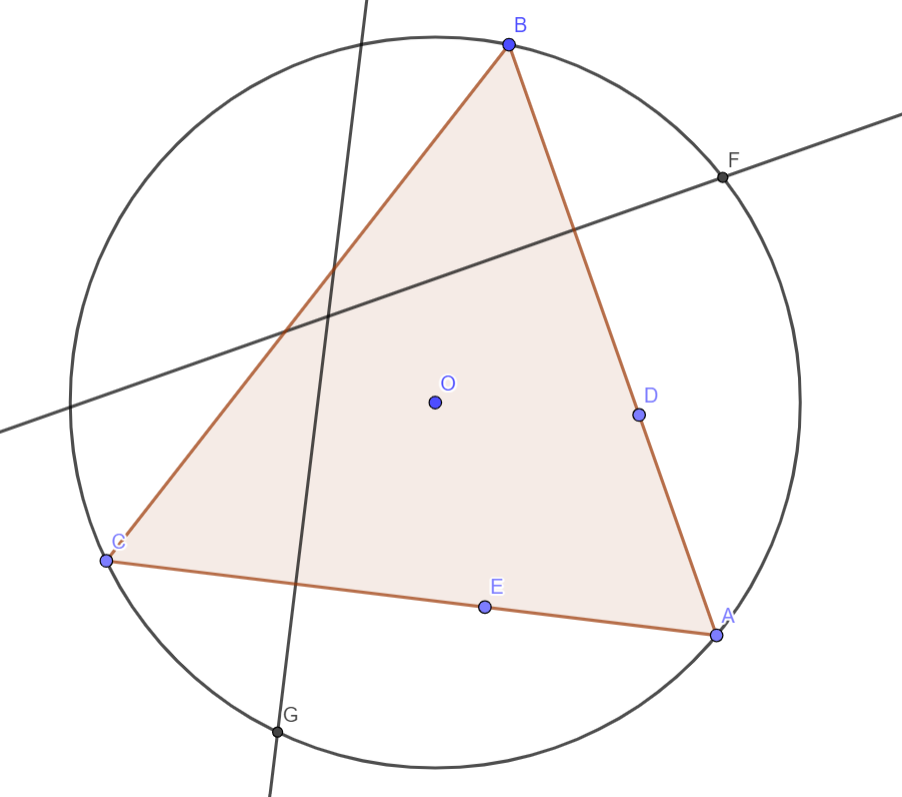
Достаточно доказать, что биссектриса угла перпендикулярна прямой
– поскольку
равнобедренный треугольник,
перпендикулярна этой биссектрисе. Перпендикулярность равносильна тому, что
или
Рассмотрим треугольник
. В нем
Аналогично,
Поэтому, исходная
задача равносильна утверждению о том, что
Отметим, что оба угла меньше так как каждый является полуразностью двух дуг, про которые известно, что их полусумма меньше
(на дуги
и
опираются углы остроугольного треугольника). Синус является инъективной функцией на отрезке
и так
как про углы известно, что они острые, достаточно лишь показать равенство их синусов:
Для этого, применим
теорему синусов к треугольникам
и
Заметим, что все шесть отношений на самом деле равны так как удвоенному радиусу
аналогично
= удвоенному радиусу
В частности,
и, так как
что и
требовалось доказать.
Ошибка.
Попробуйте повторить позже
В остроугольном треугольнике проведена высота
На сторонах
и
выбраны точки
и
соответственно таким
образом, что
— биссектриса угла
а
Докажите, что
Обозначим Тогда
![]()
Распишем теорему синусов для треугольников и
и получим:
Ошибка.
Попробуйте повторить позже
Вписанная в треугольник окружность с центром
касается сторон
в точках
соответственно. Точка
—
середина
Докажите, что прямые
и
пересекаются в одной точке.
Обозначим точку пересечения буквой
а точку пересечения
буквой
По условию просят доказать, что это
на самом деле одна и та же точка. Докажем тогда, что
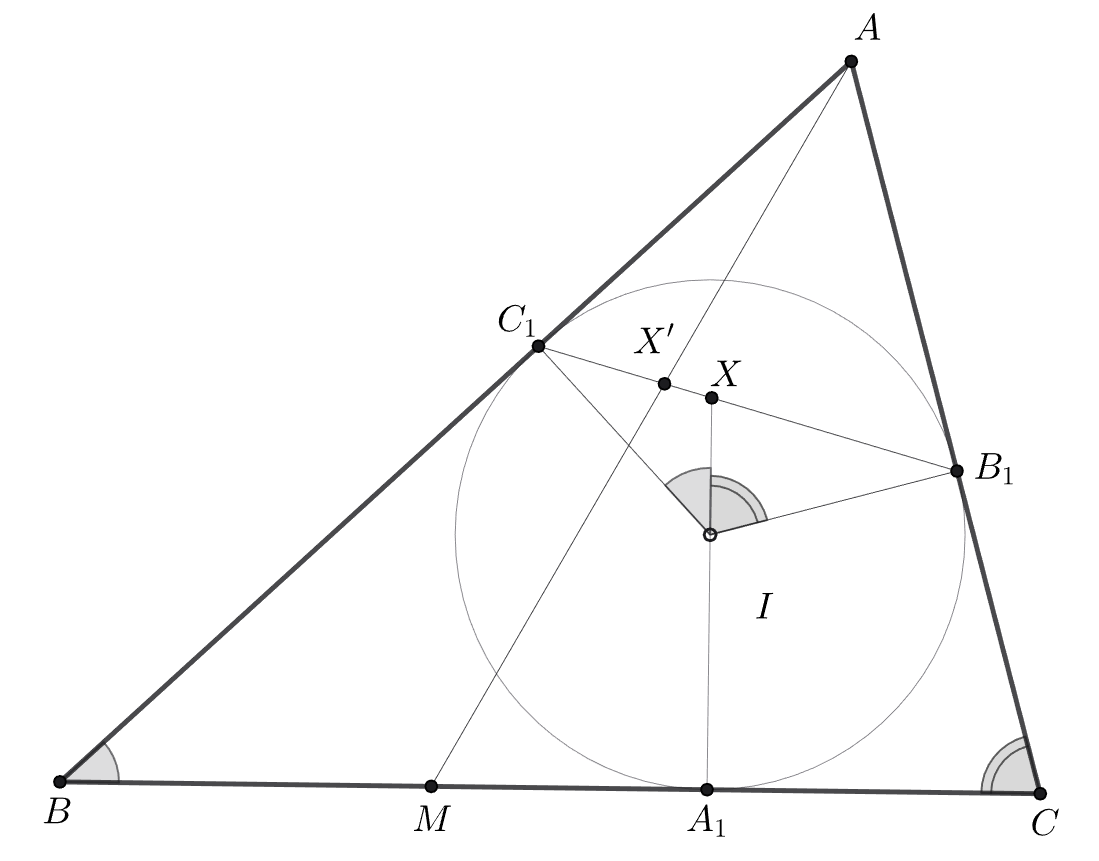
Для этого посчитаем всё в синусах:
Ошибка.
Попробуйте повторить позже
На плоскости даны два треугольника и
Через точку
проведена прямая
параллельная
Аналогично
определены прямые
и
Оказалось, что
и
пересекаются в одной точке. Пусть
— прямая, проходящая через
параллельно
Аналогично определены прямые
и
Докажите, что
и
также пересекаются в одной
точке.
![]()
Распишем синусную теорему Чевы для треугольника
По обратной синусной теореме Чевы для треугольника получаем, что
и
пересекаются в одной
точке.
Ошибка.
Попробуйте повторить позже
В остроугольном треугольнике точка
— центр описанной окружности;
— высота. Докажите, что, если
то
Пусть — радиус описанной окружности,
— середина
![]()
Докажем, что
Применим теорему синусов для
Поскольку то
что верно в силу ограниченности синуса. Т.е. мы доказали, что
Ошибка.
Попробуйте повторить позже
Точка не лежит на сторонах и их продолжениях треугольника
— точка пересечения прямой
с перпендикуляром к
проходящим через точку
Аналогично определяются точки
Докажите, что точки
лежат на одной
прямой.
Наша цель — доказать, что для треугольника и точек
на его сторонах выполнена теорема Менелая
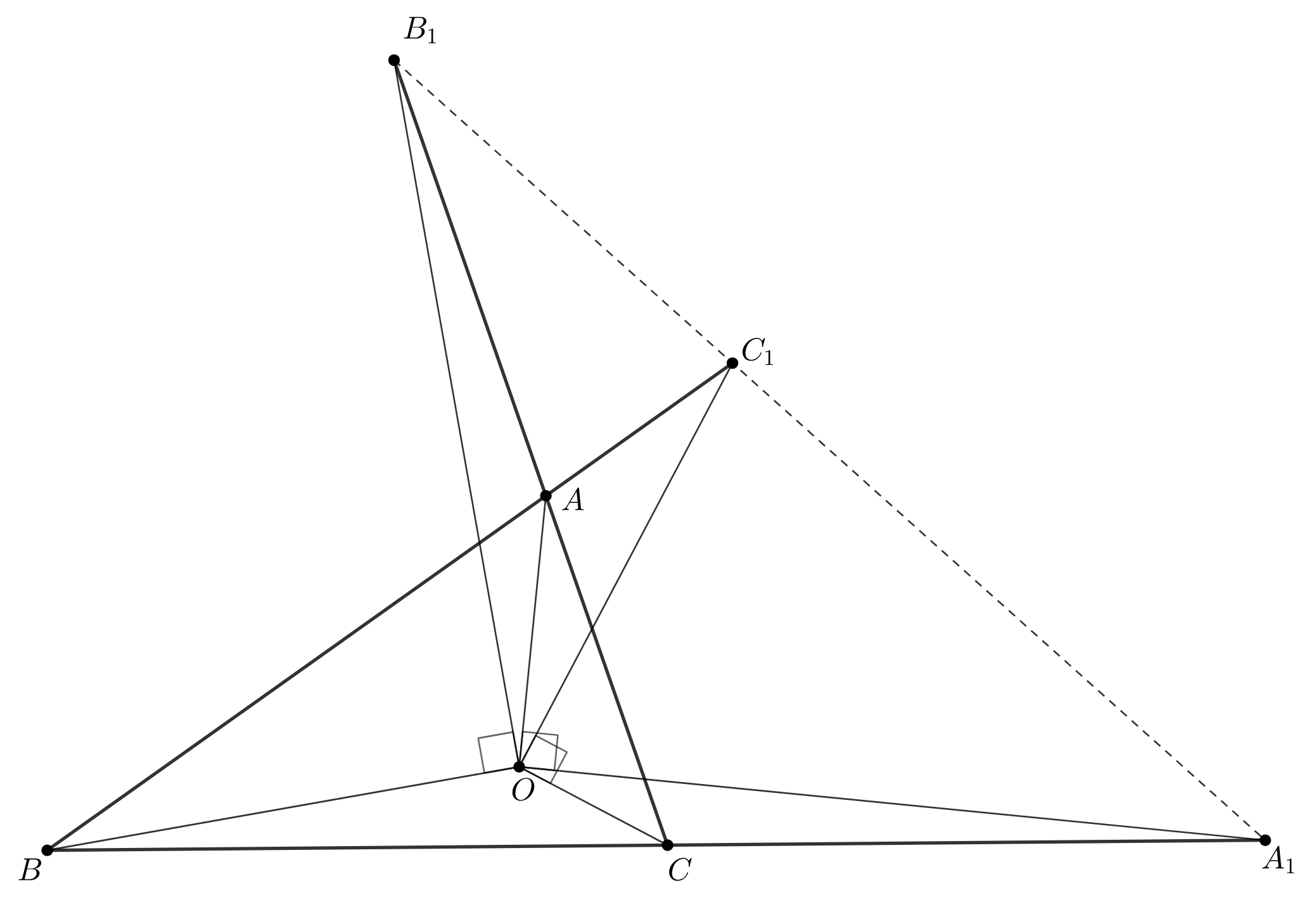
Начнём считать в синусах.
Для треугольника
Для треугольника
Наконец, отношение имеет вид
Выражая аналогично все отношения искомого произведения, получим, что достаточно доказать справделивость равенства
А ведь по синусной теоремы Чевы для треугольника и чевиан
выполнено соотношение
Тем самым, осталось доказать, что выполнено соотношение
Заметим, что откуда следует равенство
Аналогично заключаем
равенства
и
Таким образом, произведение числителей равно произведению
знаменателей.
Ошибка.
Попробуйте повторить позже
(Свойство внешней биссектрисы) В треугольнике провели внешнюю биссектрису
(
лежит на продолжении
за
точку
). Докажите, что
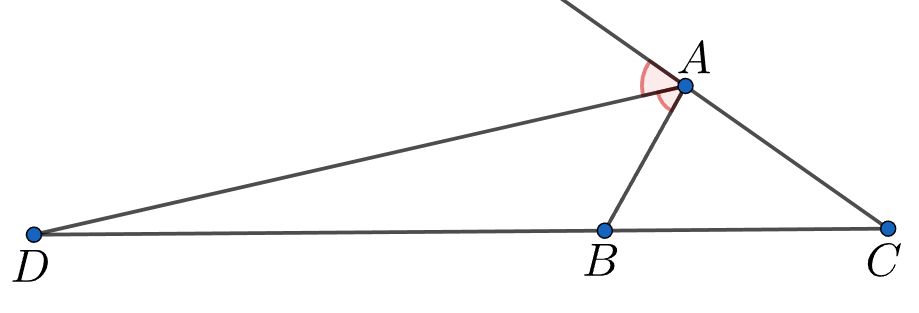
Заметим, что потому что у них общая высота. Распишем теперь эти площади через синус угла при вершине
:
Осталось заметить, что углы и
в сумме даёт
то есть они равны. Сокращаем на синусы и
получаем, что
Что и требовалось.



