Счёт в синусах и просто теорема синусов
Ошибка.
Попробуйте повторить позже
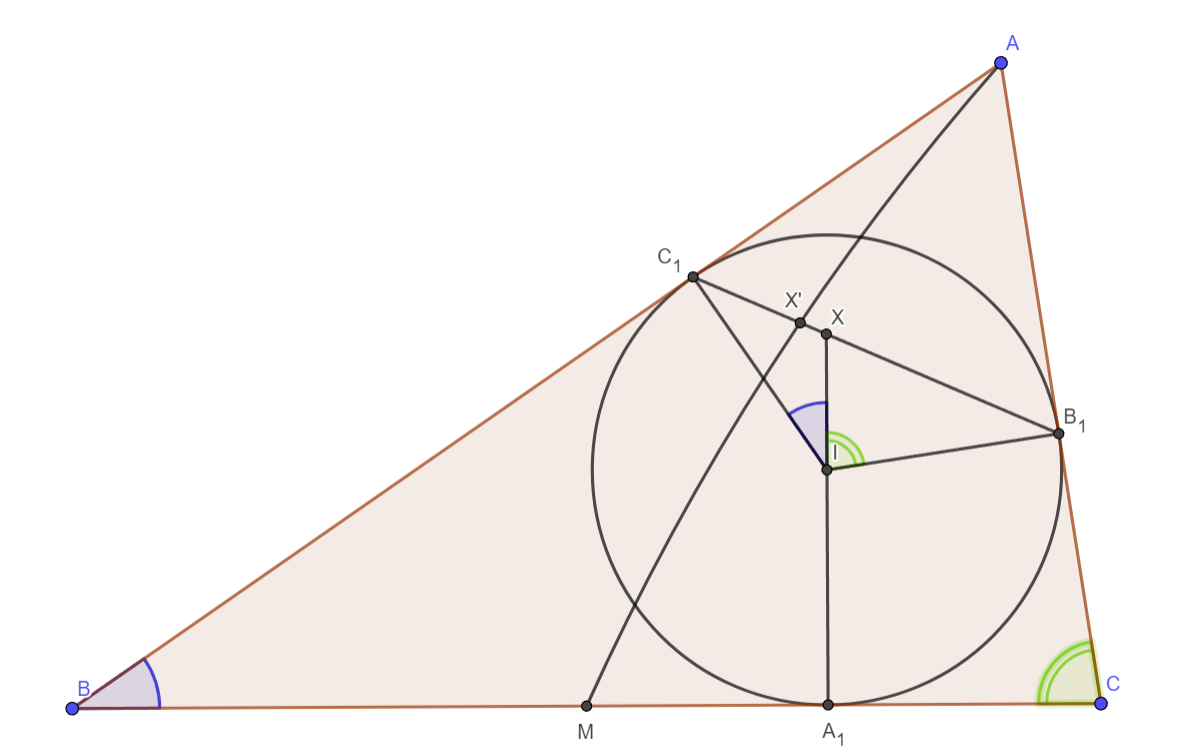
Вписанная в треугольник окружность с центром
касается сторон
в точках
соответственно. Точка
—
середина
Докажите, что прямые
и
пересекаются в одной точке.
Подсказка 1
Одно из типичных доказательств для того, что три прямые пересекаются в одной точки, — пересечь две прямые, и показать что третья там же. Удобнее всего показывать, что АМ пересекает В₁С₁ там же, где и А₁I пересекает В₁С₁. То есть если X₁ = А₁I ∩ В₁С₁ и X₂ = АМ ∩ В₁С₁ , то хотим X₁ = X₂, самое простое — показать, что они делят В₁С₁ в одинаковом отношение. Попробуйте использовать теорему синусов, ведь на чертеже много равных отрезков, например, равенство радиусов, отрезков касательных и отрезков, на которые медиана делит сторону.
Подсказка 2
С₁X₁ лежит напротив ∠С₁IX₁, а чему он равен? Что мы знаем про углы между радиусом, проведённым в точку касания, и касательной? Тогда из трёх теорем синусов для △С₁IX₁, △В₁IX₁ и △АВС выразите отношение С₁X₁/X₁В₁ через что-то, что есть на чертеже с АМ и X₂ без А₁I и X₁.
Подсказка 3
Для △С₁IX₁ и △В₁IX₁ верно, что С₁I = В₁I. Также sin(∠С₁X₁I) = sin(180° - ∠С₁X₁I) = sin(∠B₁X₁I). Тогда, используя теорему синусов для △АВС, равенство ∠С = ∠B₁IX₁ и ∠B = ∠С₁IX₁, С₁X₁/X₁В₁ выражается через АВ и АС.
Подсказка 4
Для нахождения отношения С₁X₂/X₂В₁, используйте теоремы синусов для △АС₁X₂, △АВ₁X₂, △АВМ и △АСМ. И не забывайте факт, что sin(∠β) = sin(180° - ∠β).
Обозначим точку пересечения буквой
а точку пересечения
буквой
По условию просят доказать, что это
на самом деле одна и та же точка. Докажем тогда, что
Для этого посчитаем всё в синусах:
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




