Счёт в синусах и просто теорема синусов
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
На сторонах 
и 
вписанного четырехугольника 
выбраны точки 
соответственно. Оказалось, что
четырехугольник 
является ромбом с 
и 
Обозначим через 
вписанные окружности
треугольников 
и 
соответственно. Докажите, что общие внутренние касательные к 
и 
и общие
внутренние касательные к 
и 
пересекаются в одной точке.
Подсказка 1:
Для начала давайте соберём побольше информации про рисунок. Пусть S - точка пересечения внутренних касательных окружностей (AKN) и (CLM). Например, точно можно сказать, что они гомотетичны. А какие ещё объекты связывает эта гомотетия?
Подсказка 2:
Рассмотрите прямую, проходящую через S параллельно KL, пересекающую LM в S_C, KN в S_A. Что можно сказать про отношение S_AS к SS_C? Оно как-то связано с радиусами вышеупомянутых окружностей. А если рассмотреть аналогичные прямую и отношение для точек B и D?
Подсказка 3:
Вероятно, вы пришли к тому, что SS_A относится к SS_C так же, как радиусы вписанных окружностей AKN и CML. Давайте поймём, что если доказать аналогичный факт для аналогичных объектов, связанных с точками B и D, то задача будет решена.
Подсказка 4:
Действительно, применяя аналогичные рассуждения к точке пересечения S' внутренних общих касательных к BKL и NMD, мы увидим, что S' удовлетворяет аналогичным соотношениям, и внутри KLMN существует единственная точка, удовлетворяющая им. Следовательно, S′ = S. Как же теперь прийти к желаемому соотношению?
Подсказка 5:
Давайте заметим, что S_BS к S_DS относятся так же, как KS_A к S_AN. С этим отношением работать проще.
Подсказка 6:
Для доказательства стоит обратить внимание на четырёхугольник, который получится соединением треугольников AKN и LCM. Основная идея доказательства - это связь отношения отрезков и площади треугольников. А дальше счёт!
Пусть 
— центр 
а 
— его радиус для 
Обозначим через 
и 
точки касания 
и 
с 
и 
соответственно. Предположим, что внутренние общие касательные к 
и 
пересекаются в точке 
, которая является центром
гомотетии 
с отрицательным коэффициентом (а именно, с коэффициентом 
), переводящей 
в 
Эта гомотетия переводит
в 
(так как касательные к 
и 
в точках 
и 
параллельны), следовательно, 
— точка на отрезке 
с
Построим отрезки 
и 
через 
с 
и 
Обратим внимание, что
переводит 
в 
следовательно, 
и 
Докажем, что 
или, что то же самое, 
Это докажет утверждение задачи; действительно, применяя аналогичные
рассуждения к точке пересечения 
внутренних общих касательных к 
и 
мы увидим, что 
удовлетворяет
аналогичным соотношениям, и внутри 
существует единственная точка, удовлетворяющая им. Следовательно,
Далее обозначим через 
и 
инцентры и радиусы вписанных окружностей треугольников 
и
соответственно. Треугольник 
можно сдвинуть на 
чтобы склеить его с треугольником 
в четырехугольник
подобный 
В частности, это показывает, что 
аналогично 
Более того, тот же сдвиг
переводит 
в 
а также 
в инцентр 
треугольника 
Поскольку 
точки 
лежат на
одной прямой. Таким образом, для завершения решения достаточно применить к четырехугольнику 
следующую
лемму.
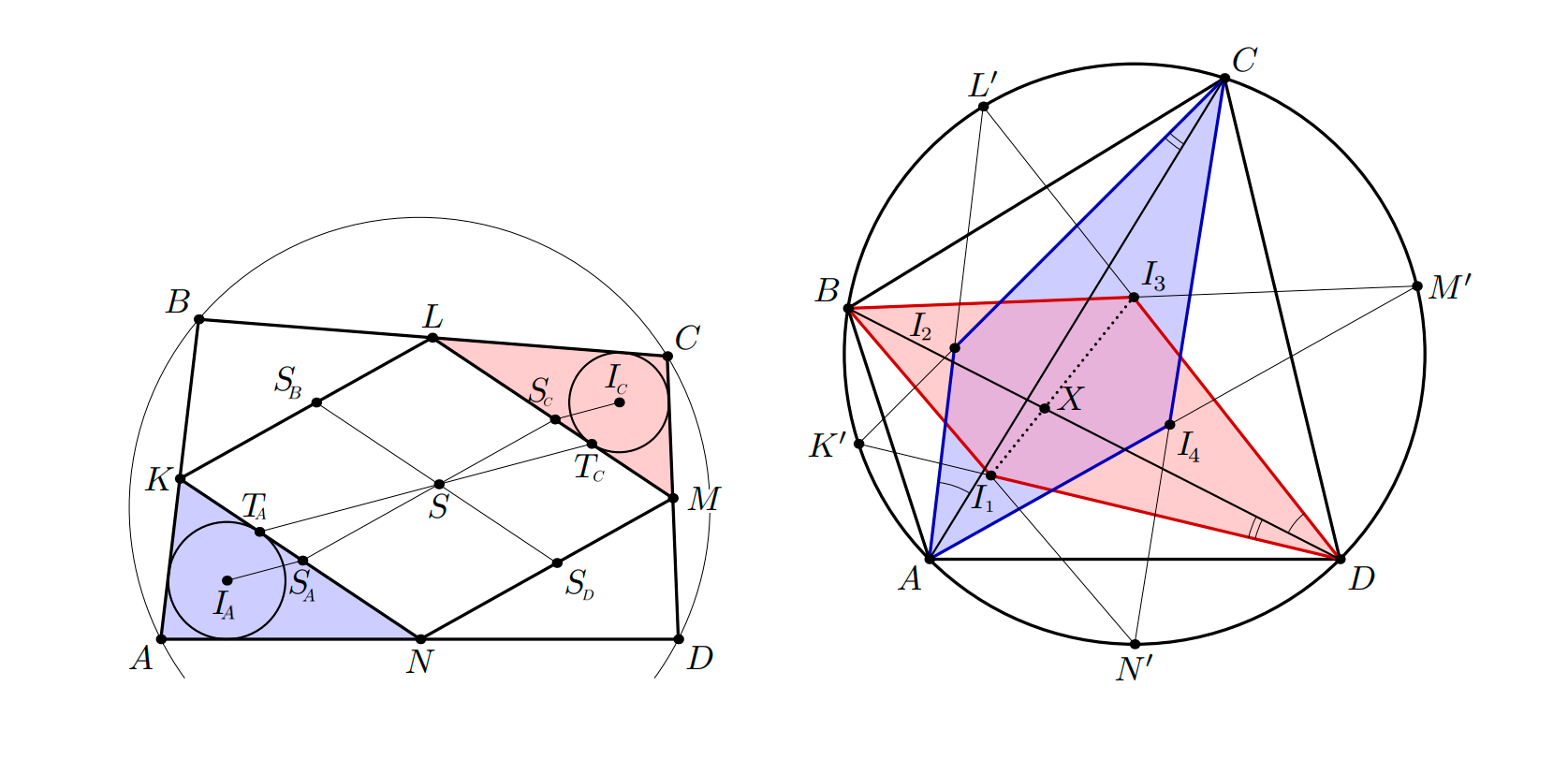
Лемма. Пусть 
— вписанный четырехугольник, и определим 
и 
как выше. Пусть 
пересекается с 
в точке
Тогда 
Доказательство леммы. Пусть в описанной окружности 
и 
— середины дуг 
и 
не
содержащих других вершин 
соответственно. Таким образом, 
и т. д. В дальнейших вычислениях мы обозначим за
![[P]](/api/latex-service/v1/GetSession/141223/index-0eade2dcb7390ba3ad06ec6f6dc7b0bd.svg)
площадь многоугольника 
Используя подобия 
и т.п., а также равенства треугольников 
и
(например, выполнено первое равенство, поскольку 
– общая биссектриса углов 
и 
),
получаем:
![BX- [I1BI3] BI1⋅BI3⋅sinI1BI3 -BI1 BI3 sin-N′BM-′
DX = [I1DI3] = DI1⋅DI3⋅sinI1DI3 =DI1 ⋅CI3 ⋅ sinK′DL′
BK-′ -BL′ sinN′DM-′ -BK′⋅BL-′⋅sinK-′BL-′- sin2N′DM-′
= DN ′ ⋅DM ′ ⋅ sinK ′BL ′ = DN ′⋅DM ′⋅sin N′DM ′ ⋅sin2K ′BL′
[K ′BL′] N ′M ′2 [K′BL′]⋅ AKC′L2′2 [AI2C] r2
= [M′DN-′] ⋅-K′L′2 = [M-′DN′]⋅ AC′2′2-= [AI4C] = r4,
NM](/api/latex-service/v1/GetSession/141223/index-4e74701ff0febb451cac2fe12e28caf4.svg)
что и заканчивает наше доказательство.
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
