Построения циркулем и линейкой
Ошибка.
Попробуйте повторить позже
Постройте треугольник по двум сторонам и разности противолежащих им углов.
Подсказка 1
Какая фигура использует всё, что нам известно: два отрезка заданной длины, угол, который является разностью других углов на картинке?
Подсказка 2
Равнобедренная трапеция! Построим треугольник с двумя заданными сторонами и углом между ними(тот, что в условии). Что нужно сделать, чтобы прийти к трапеции?
Подсказка 3
Опишем около него окружность) Теперь через одну из точек проведем прямую, параллельную другой на картинке, построим трапецию, вписанную в имеющуюся окружность и найдем треугольник, нужный нам!
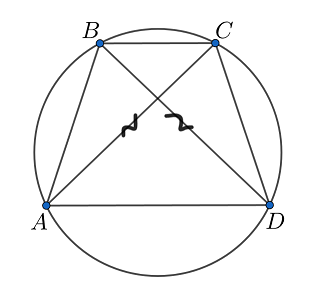
Пусть отрезок — меньшая сторона из двух данных, отложим от неё угол
равный данной разности (точку
отметим так,
что отрезок
равен по длине большей стороне). Опишем окружность около треугольника
(строим серединные перпендикуляры к
двум сторонам, их точка пересечения — центр окружности). Теперь проведём через точку
прямую, параллельную
Пусть она
пересекает окружность в точке
Заметим, что трапеция равнобедренная, а значит
, а угол
равен разности углов
и
.
Следовательно, треугольник
— искомый.
Догадаться до решения можно, если вспомнить про равнобедренную трапецию и увидеть, что там присутствует угол, равный разности нужных нам углов.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




