Построения циркулем и линейкой
Ошибка.
Попробуйте повторить позже
На каждой стороне квадрата отметили по точке. Затем все, кроме этих точек, стерли. Восстановите квадрат с помощью циркуля и линейки
Подсказка 1
Пусть данные точки K, P, R, Q лежат на сторонах AB, BC, CD, AD искомого квадрата ABCD. Отрезок KP виден из точки B под прямым углом ⇒ точка B лежит на окружности, построенной на KP как на диаметре. Аналогично с точкой D. Какой хороший отрезок теперь можно провести?
Подсказка 2
Проведём диагональ BD. Пусть она повторно пересекает окружность, содержащую B, в точке M, а содержащую D — в точке N. BD делит углы KBP и RDQ пополам ⇒ точки M и N — середины полуокружностей KMP и RNQ. Как отсюда вытекает способ построения квадрата?
Подсказка 3
Пусть искомые точки — K, P, R, Q (в указанном порядке). Тогда построим на отрезках KP и RQ как на диаметрах окружности. Если M и N — середины полуокружностей, обращённых друг к другу, то диагональ квадрата лежит на прямой MN. Далее легко достраивается весь квадрат. Всегда ли задача имеет единственное решение?
Подсказка 4
На самом деле если M не совпадает с N, то задача имеет единственное решение, но в противном случае решений бесконечно много!
Предположим, что данные точки и
расположены на сторонах соответственно
и
искомого квадрата
Поскольку отрезок
виден из точки B под прямым углом, то эта точка лежит на окружности с диаметром
Аналогично точка
лежит на окружности с диаметром
Пусть диагональ
квадрата вторично пересекает первую окружность в точке
а вторую —
в точке
Поскольку диагональ квадрата делит его угол пополам, то точки
и
— середины соответствующих
полуокружностей.
Отсюда вытекает следующий способ построения. Пусть — данные точки (в указанном порядке). Построим на отрезках
и
как на диаметрах окружности. Пусть
и
— середины полуокружностей, обращённых друг к другу. Диагональ квадрата лежит
на прямой
Дальнейшие действия очевидны.
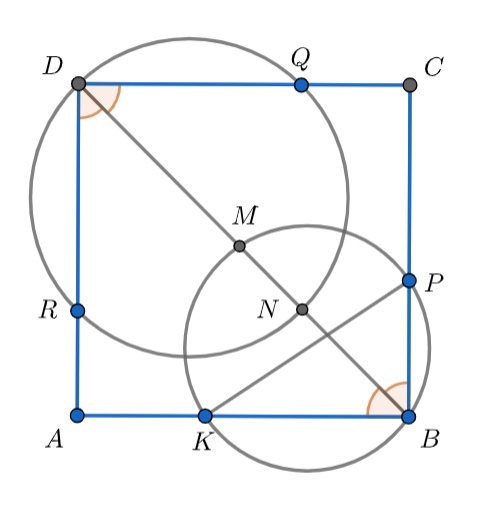
Если точки и
не совпадают, то задача имеет единственное решение. В противном случае задача имеет бесконечно много
решений.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




