Построения циркулем и линейкой
Ошибка.
Попробуйте повторить позже
равных отрезков для любого натурального 
с помощью циркуля и
линейки.
равных углов для любого натурального 
с помощью циркуля и
линейки.
(a) Для начала делим отрезок 
пополам — точка 
(мы знаем, как это сделать с помощью циркуля и линейки), затем каждый из
получившихся отрезков ещё пополам — точки 
и 
и т.д. Таким образом, каждый раз количество отрезков (равных)
удваивается. Так как изначально был 
отрезок, мы сможем разделить его на 
отрезков при любом натуральном 
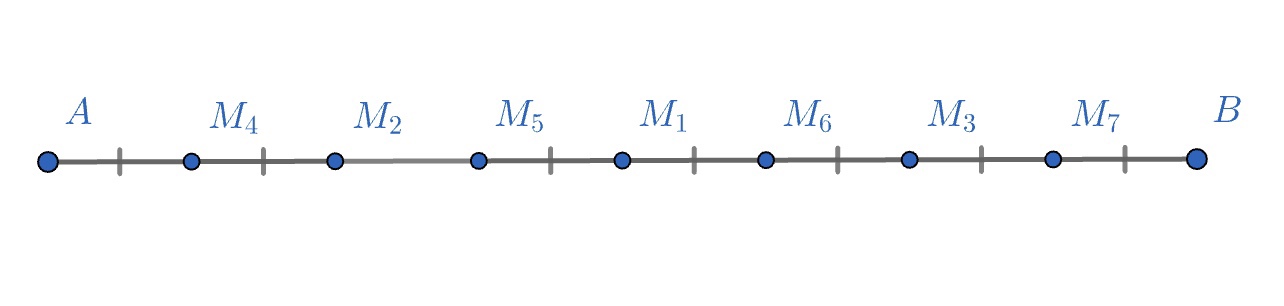
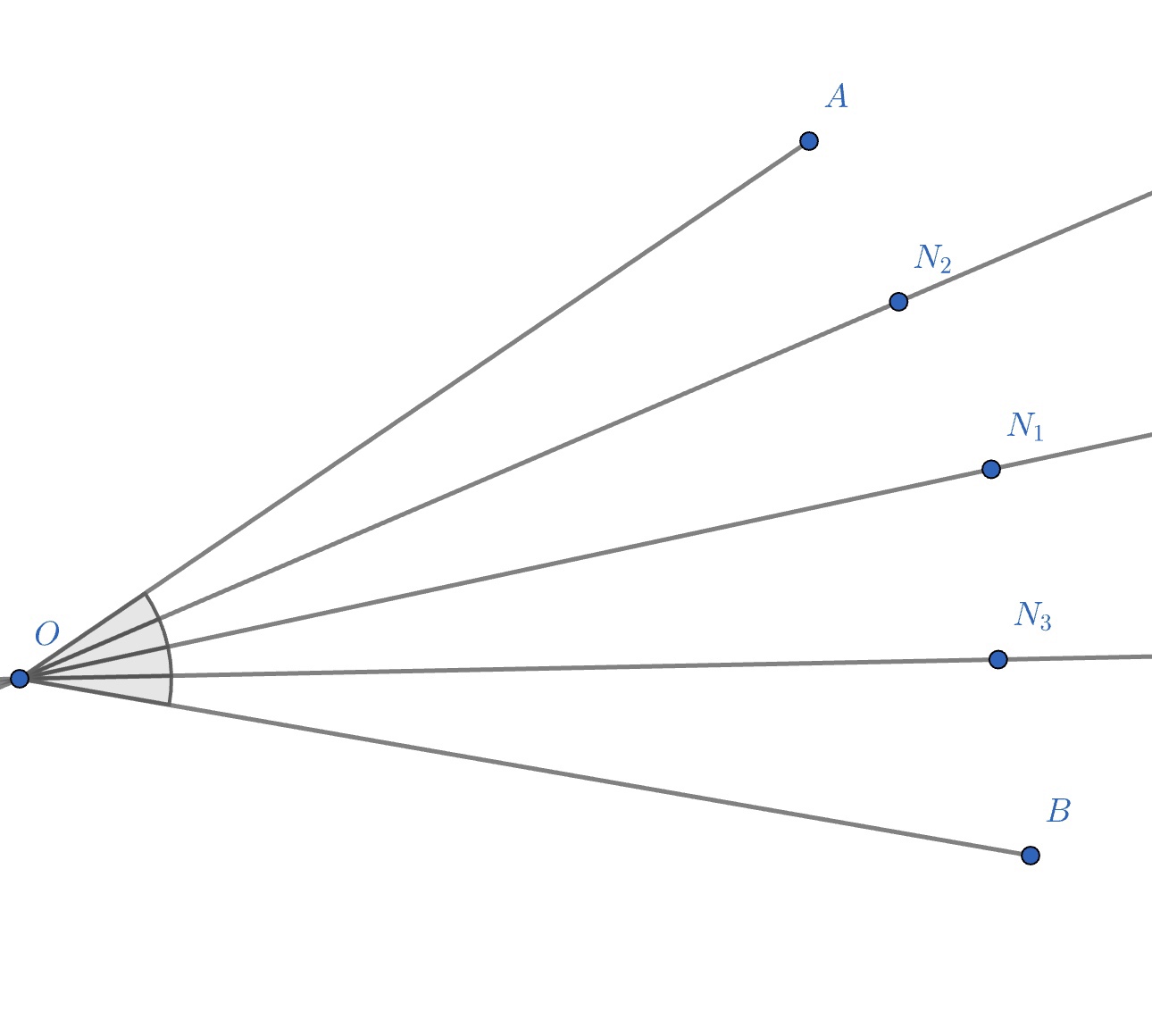
(b) Аналогично пункту 
мы знаем, как поделить угол на 
равных (проводим биссектрису) с помощью циркуля и линейки. Тогда
угол 
делим на 2 равных — 
и 
Далее делим каждый из получившихся углов ещё на два равных и т.д. Таким
образом, каждый раз количество углов (равных) удваивается. Так как изначально был 
угол, мы сможем разделить его на 
угла при
любом натуральном 
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
