Функции на Иннополисе
Ошибка.
Попробуйте повторить позже
Рассмотрим уравнение 
на множестве положительных действительных чисел. Вам требуется явно указать для каждого
вещественного значения 
число таких различных вещественных чисел 
что 
(Пример явного описания: для 
существует единственное число 
такое, что 
Источники:
Подсказка 1
Случай x = 1 уже описан в формулировке задачи. Будем далее полагать, что x ≠ 1 и y ≠ 1. Какие методы решения подобных уравнений Вам знакомы?
Подсказка 2
У нас показательное уравнение. Попробуйте взять логарифм от обеих частей.
Подсказка 3
Мы получим x ⋅ ln(y) = y ⋅ ln(x). И слева, и справа x и y. Давайте перегруппируем множители.
Подсказка 4
Разделим обе части на xy, получим ln(x)/x = ln(y)/y. Видите ли Вы здесь какую-нибудь функцию?
Подсказка 5
Вообще говоря, из нашего уравнения следует, что x/ln(x) = y/ln(y). Рассмотрите функцию f(z) = z/ln(z). Попробуйте построить её график.
Подсказка 6
Чтобы определить области возрастания и убывания f(z), возьмем её производную. Получится (ln(z) - 1) / ln²(z).
Подсказка 7
На интервале (0; 1) функция f убывает от 0 до -∞, на интервале (1; e) f тоже убывает, достигая локального минимума f(e) = e. Потом на интервале (e; +∞) возрастает от e до +∞. Теперь возьмите x > 0 и попробуйте подвести итоги.
Подсказка 8
Например, если 0 < x < 1, то (x / ln(x)) < 0 и функция непрерывно убывает, следовательно (чтобы в этом убедиться, можно нарисовать график), будет единственное подходящее нам вещественное y. Аналогично с остальными промежутками.
Случай 
уже описан в формулировке задачи, поэтому в дальнейшем мы можем предполагать, что 
и 
Возьмем натуральный логарифм от обеих частей исходного уравнения и получим следующее уравнение
Так как 
и 
то это уравнение равносильно новому уравнению
Проанализируем функцию 
и построим ее график. Так как
то на интервале 
функция 
убывает от 
до 
на интервале 
функция 
тоже убывает, достигая локального
минимума 
при 
а потом на интервале 
возрастает от 
до 
Подведём итоги. Пусть 
— произвольное положительное действительное число. Имеем:
- если
то 
и, следовательно, (см. график) существует только единственное подходящее нам вещественное
число 
- если
то, как это уже было сказано, существует только единственное подходящее вещественное число 
- если
или если 
то 
и, следовательно, (см. график) существуют два подходящих вещественных
числа 
- если
то 
и, следовательно, (см. график) существует единственное подходящее вещественное число 
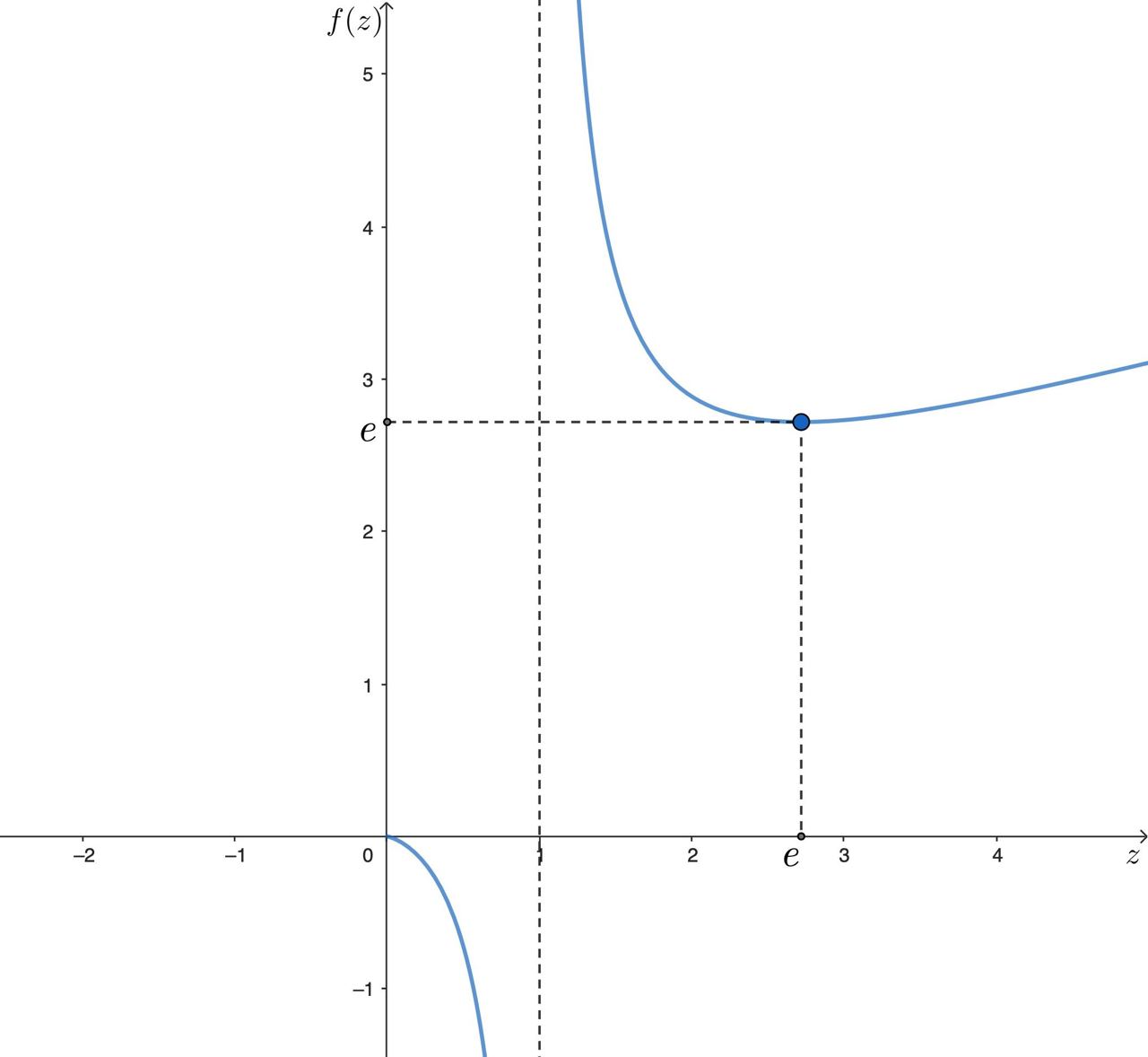
При ![x∈ (0;1]∪e](/api/latex-service/v1/GetSession/257617/index-e45381b0c0c7daa61ec0d873cd8ab766.svg)
— одно решение; при 
— два решения
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
