Отбор Всесиба
Ошибка.
Попробуйте повторить позже
На отрезке , как на диаметре, построен полукруг, в котором точка
середина дуги
. На дуге
выбрана произвольная
точка
, отличная от
и
, через
обозначена точка пересечения прямых
и
. Пусть
— точка пересечения
прямой
и перпендикуляра к прямой
, проведённого через точку
. Докажите, что длины отрезков
и
равны.
Подсказка 1
Первое, что бросается в глаза — большое количество прямых углов на картинке. Прямой ВРТ говорит о том, что для решения задачи достаточно доказать, что угол ТВР, например, равен 45 градусам. Что ещё, связанное со вписанностью и прямыми углами, можно указать на картинке?
Подсказка 2
Хочется показать, что на картинке имеется вписанный четырехугольник, используя один из признаков такого четырехугольника. Также осталось вспомнить, что точка М — середина дуги АВ окружности, это тоже важно для некоторых углов!
Для начала заметим, что так как
— диаметр полуокружности. По условию прямая
— перпендикуляр к
, то
есть
Тогда в четырехугольнике
внутренний угол
равен внешнему углу
при противоположной вершине.
Значит, четырёхугольник
вписанный.
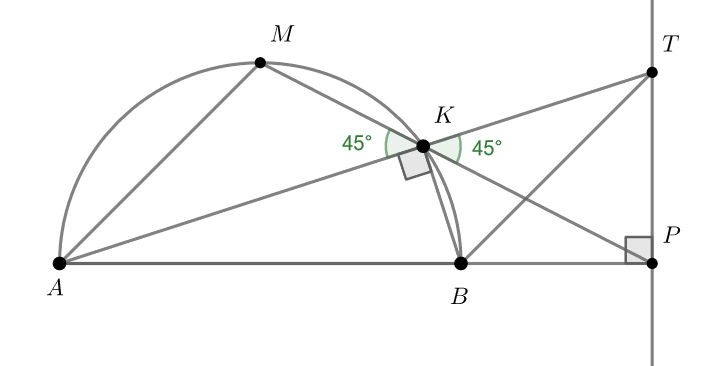
Так как — середина полуокружности,
а опирающийся на эту дугу вписанный угол
как вертикальные углы, а
потому что
— вписанный четырехугольник.
Тогда то есть прямоугольный треугольник
имеет угол в
Значит,
—
равнобедренный и
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




