Неравенство ломаной
Ошибка.
Попробуйте повторить позже
В пространстве даны скрещивающиеся перпендикулярные прямые и
Точки
и
— середины отрезков
и
соответственно. Докажите, что
Источники:
Подсказка 1:
Давайте перенесём EF в левую часть неравенства и будем доказывать в таком формате. Попробуйте ввести некоторые обозначения, чтобы левую часть неравенства можно было записать в более удобном виде.
Подсказка 2:
Деление на 2 намекает, что стоит обозначить через M и N середины AD и BC.
Подсказка 3:
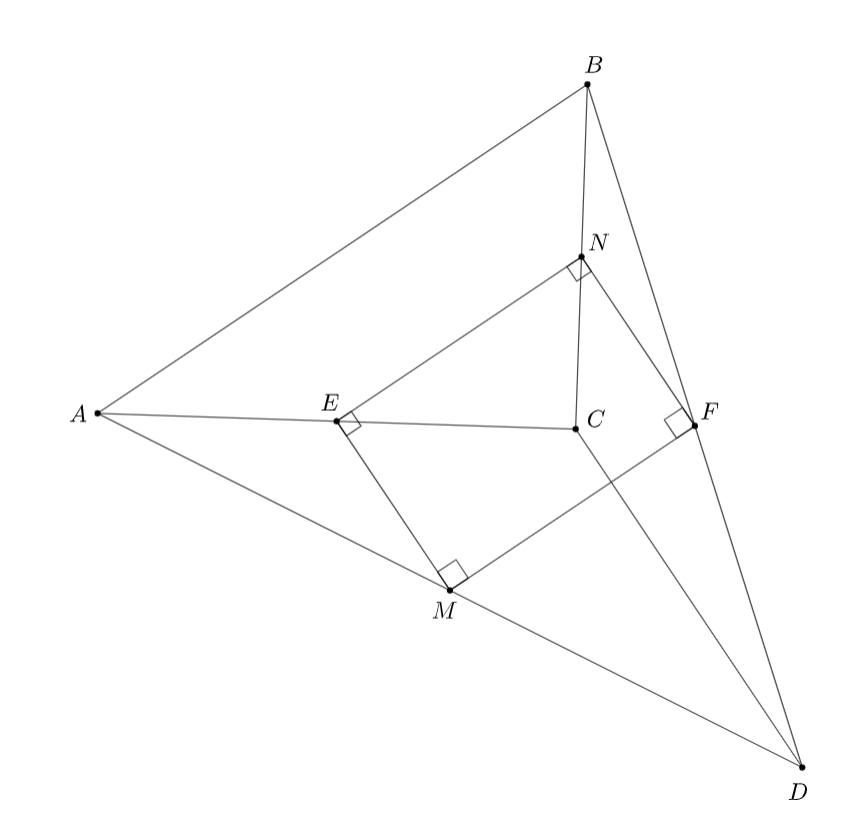
Обратите внимание на четырехугольник MENF. Что про него можно сказать? Не забывайте про перпендикулярность из условия.
Подсказка 4:
MENF — прямоугольник. Используя это, попробуйте превратить левую часть неравенства в сумму звеньев ломаной, которая начинается и заканчивается в BD.
Подсказка 5:
Не забывайте, у прямоугольника диагонали равны.
Обозначим через и
середины отрезков
и
Тогда
— средняя линия в треугольнике
а
— в
треугольнике
Следовательно,
Аналогично
Таким образом, точки
лежат в одной
плоскости, причём из условия
следует, что
— прямоугольник. Значит, равны его диагонали
и
Заметим, что
по неравенству ломаной, остаётся вычесть из обеих частей.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




