Разбиение доски на части
Ошибка.
Попробуйте повторить позже
Назовём расстоянием между двумя клетками клетчатой доски наименьшее количество ходов, за которое шахматный король может
добраться от одной из них до другой. Найдите наибольшее количество клеток, которое можно отметить на доске так, чтобы
среди них не нашлось двух клеток, расстояние между которыми равно
Источники:
Разобьём доску на квадратов
прямоугольников
и один квадрат
(см. рис. слева). В каждом квадрате
клетки разбиваются на
четвёрок так, что расстояние между любыми клетками в одной четвёрке равно
(каждая
четвёрка состоит из клеток с координатами
). Тогда в любой четвёрке может
быть отмечено не более одной клетки, то есть общее число отмеченных клеток в таком квадрате не превосходит
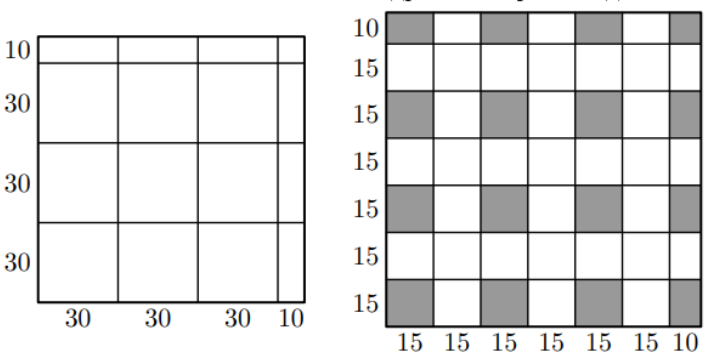
Аналогично, каждый прямоугольник (скажем, с длинной горизонтальной стороной) разбивается на пары клеток, отстоящих
друг от друга на
(с координатами
и
) — поэтому в нём не более
отмеченных клеток. Наконец, в квадрате
всего
клеток. Итого, отмеченных клеток не больше, чем
Пример с таким количеством отмеченных клеток показан на рис. справа.
клеток
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




