Регион 11 класс
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
В каждой клетке доски лежит по рублёвой монете. Даша и Соня играют, делая ходы по очереди, начинает Даша. За один ход
можно выбрать любую монету и передвинуть её: Даша двигает монету на соседнюю по диагонали клетку, Соня — на соседнюю по стороне.
Если две монеты оказываются в одной клетке, одна из них тут же снимается с доски и достаётся Соне. Соня может остановить игру
в любой момент и забрать все полученные деньги. Какой наибольший выигрыш она может получить, как бы ни играла
Даша?
Источники:
Подсказка 1:
Чтобы придумать стратегию за Соню, попробуйте разбить доску на какие-нибудь маленькие части, в рамках которых она сможет легко получать монеты.
Подсказка 2:
Разбейте на квадраты 2 на 2. Давайте заметим, что если в таком квадрате есть хотя бы 2 монеты, то Соня легко сможет получить одну из них (почему?). Исходя из этого, можно понять, каким будет ответ.
Подсказка 3:
Итак, скорее всего вы поняли, что ответ будет 300. Осталось придумать стратегию за Дашу, с помощью которой она всегда сможет сохранить 100 монет на доске. Попробуйте выбрать 100 монет, находящихся в каких-то определённых столбцах.
Подсказка 4:
Будет здорово, если эти столбцы не будут рядом. Тогда Соне будет сложнее забрать какую-то из выбранных монет. Значит, можно взять, например, нечётные столбцы и придумать стратегию, при которой после каждого хода Даши выбранные монеты находятся в этих столбцах.
Сначала приведём стратегию за Соню. Пока она не получила больше 299 монет, перед её ходом на доске остаётся хотя бы 101 монета.
Разобьем доску на 100 квадратов Получается, что какие-то две монеты лежат в одном и том же квадрате
Если эти две
монеты соседние по стороне, то Соня надвигает одну на другую, и получает ещё одну монету. Если они стоят по диагонали, то Соня сдвигает
одну из них в столбец к другой (здесь и далее столбец имеет длину 2, строка — длину 200). Теперь, какой бы ход ни сделала Даша, эти две
монетки всё ещё будут соседними по стороне (либо одна будет снята и уйдёт в доход Сони), значит, своим следующим ходом Соня
сможет получить ещё одну монетку. Таким образом, Соня всегда сможет увеличивать свой выигрыш, пока он меньше
300.
Теперь покажем, как играть за Дашу, чтобы Соня не получила больше 300 монет. Пронумеруем столбцы числами от 1 до 200 по порядку, выберем в каждом нечётном столбце по одной монетке и мысленно покрасим их в красный цвет. Даше достаточно обеспечить, чтобы красные монетки всегда оставались на доске. Для этого, в свою очередь, достаточно, чтобы две красные монеты никогда не попадали в одну клетку, потому что когда в клетку попадают красная и не красная монеты, можно считать, что с доски снимается не красная.
Назовём расположение монет на доске стабильным, если по одной красной монете лежит в столбцах а
ещё одна располагается в одном из двух последних столбцов 199, 200. Легко видеть, что после любого хода из стабильной
позиции две красные монеты не окажутся в одной клетке. Даша будет играть так, чтобы после каждого её хода получалась
стабильная позиция. Если после хода Сони позиция осталась стабильной, то Даша двигает сотую красную фишку между двумя
последними столбцами, так же Даша поступит и своим первым ходом. Если же после хода Сони позиция перестала быть
стабильной, то Соня подвинула одну из красных монет из некоторого столбца
в соседний столбец. Тогда Даша своим ходом
вернёт её в столбец
Таким образом, на доске всегда останется хотя бы 100 монет, и Соня заработает не более трёхсот
рублей.
300
Ошибка.
Попробуйте повторить позже
Найдите все такие пары целых чисел и
, что
Источники:
Подсказка 1:
Давай заметим, что в правой части равенства почти полный квадрат. Не хватает 1. Давайте добавим её слева и справа.
Подсказка 2:
Также хотелось бы разложить на скобочки левую часть, притом желательно на взаимно простые. Если не получается угадать разложение, рассмотрите выражение слева как квадратный трёхчлен относительно (n-2)!.
Подсказка 3:
Итак, вы получили равенство ((n - 1)! - 1)((n - 2)! - 1) = (m - 1)². Являются ли скобки в левой части взаимно простыми?
Подсказка 4:
Для дальнейших продвижения необходимо вспомнить, что если произведение взаимно простых чисел равно квадрату, то каждое из них является квадратом. Кстати, почему это так?
Подсказка 5:
Теперь осталось показать, что при больших n какая-то из скобок не сможет быть большим квадратом. Учитывая особенности факториалов, стоит подумать про остатки. Например, при делении на 4 квадраты могут иметь далеко не все остатки.
Заметим, что
Пусть Заметим, что числа
и
взаимно просты. Предположим, что это не так, и оба этих числа делятся
на простое число
Тогда число
тоже делится на Тогда
делится на
а
не кратно
противоречие. Таким образом, произведение взаимно
простых чисел
и
—– точный квадрат, тогда и каждое из них точный квадрат. Однако, число
при
даёт остаток 3 при делении на 4, поэтому оно точным квадратом быть не может. Остаётся разобрать случаи
При
получается
решений нет. При
мы получаем:
что даёт единственное решение
,
Ошибка.
Попробуйте повторить позже
Существуют ли четыре попарно различных положительных числа при которых все четыре числа
целые?
Источники:
Подсказка 1:
Эта задача — конструктив. Придумайте пример, удовлетворяющий условию.
Подсказка 2:
Чтобы было проще достичь делимости, попробуйте сделать так, чтобы большинство знаменателей были равны 1 или -1.
Пусть ,
,
,
Тогда
Да, существуют.
Ошибка.
Попробуйте повторить позже
Вещественные числа таковы, что
Докажите, что каждое из чисел
меньше
1.
Источники:
Подсказка 1:
Создаётся впечатление, что взяли слагаемые из разложений (x - 1)², (y - 1)² и (z - 1)² и расставили их по неравенствам. Как насчёт того, чтобы сложить какие-нибудь 2 неравенства?
Подсказка 2:
Давайте сложим первые два неравенства и выделим (x - 1)² и (y - 1)². Посмотрите внимательно на оставшиеся слагаемые. Какие на них накладываются ограничения, чтобы неравенство выполнялось?
Первое решение. Сложим первые два неравенства. Преобразуя, получаем неравенство:
Следовательно, Тогда
аналогично для других двух переменных.
_________________________________________________________________________________________________________________________________________________________________________________
Второе решение. Не умаляя общности, предположим, что Тогда
Добавив к обеим частям неравенства
имеем:
откуда наибольшее из чисел Значит, и все числа меньше 1.
_________________________________________________________________________________________________________________________________________________________________________________
Третье решение. Из условия следует, что аналогично
Также
по неравенству о средних.
Значит,
аналогично
и
Не умаляя общности можно считать, что
—– минимальное из чисел
тогда
откуда
аналогично
а тогда и
Ошибка.
Попробуйте повторить позже
В треугольнике с углом
при вершине
медианы
и
пересекаются в точке
Прямая, проходящая через точку
и параллельная
пересекает описанную окружность треугольника
в точках
и
Найдите сумму углов
и
Источники:
Подсказка 1:
На рисунке имеется много параллельных прямых. Значит, можно попереносить отношения. Не забывайте, в каком отношении центр тяжести делит медианы.
Подсказка 2:
Первая подсказка намекала на то, что надо найти, как сотносятся отрезки AN, NR и RB — как 3 : 1 : 2. Теперь, используя это, попробуйте как-то поработать с окружностью.
Подсказка 3:
Поработать нужно даже не с окружностью, а со степенью точек относительно неё. Обратите внимание на точку пересечения PQ и AB (обозначим её через R).
Подсказка 4:
Пусть NR = x, RB = 2x, AN = 3x. Наверное, вы записали, что RP • RQ = RN • RA = 4x². Быть может, в выражении 4x² можно разглядеть что-то другое помимо RN • RA?
Подсказка 5:
На самом деле 4x² = BR². Это позволит некоторым образом удачно перекинуть углы и что-то понять про прямые BP и BQ в угле ABC.
Подсказка 6:
Итак, вы поняли, что BP и BQ — изогонали в угле ABC, аналогично можно сказать про прямые CQ и CR в угле ACB. Теперь осталось лишь выразить требуемую сумму углов через угол BAC.
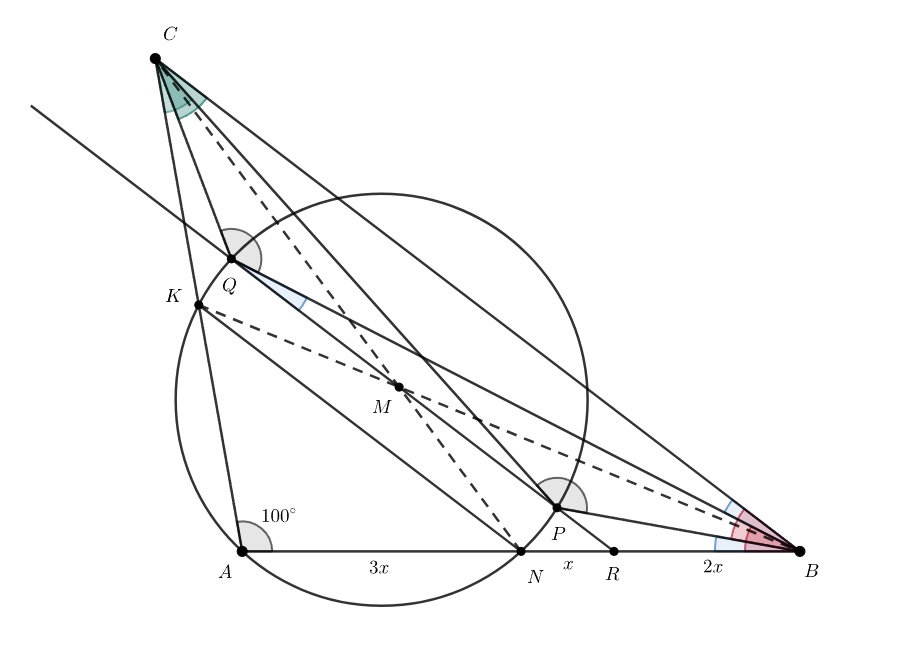
Обозначим через точку пересечения прямой
с отрезком
Заметим, что
— средняя линия треугольника
поэтому
Значит, по теореме Фалеса
последнее равенство следует из того, что — точка пересечения медиан треугольника
Обозначим Тогда
Поскольку четырёхугольник
вписанный,
имеем
Следовательно, прямая касается описанной окружности треугольника
поэтому
а тогда и
Рассуждая аналогично, получаем, что
Значит,
Ошибка.
Попробуйте повторить позже
Саша взял кусок нити. Он сложил её пополам, затем ещё раз пополам, и так 10 раз. Затем он взял ножницы и разрезал полученную конструкцию в одном месте (таким образом, он перерезал нить в 1024 местах). В итоге нить распалась на куски. Оказалось, что длины этих кусков принимают лишь два различных значения, наименьшее из которых равно 10 см. Найдите все возможные значения длины исходной нити.
Источники:
Подсказка 1:
Пусть разрез сделан в b см от правого края и в a см от левого края каждого из 1024 отрезков, в которые сложили нить до разрезания. Какие тогда значения могут принимать длины кусков нити?
Подсказка 2:
Если вы рассуждали правильно, то получили три возможных значения: a, 2a и 2b. Но по условию то их всего 2. Что это значит?
Подсказка 3:
Какие-то две совпадают. Осталось рассмотреть разные варианты совпадения длин и вычислить длину нити, учитывая, что она равна 1024(a + b).
Полученная до разрезания конструкция состоит из 1024 отрезков нити, которые нить проходит поочерёдно слева направо и справа налево
(пусть оба конца нити находятся слева). Тогда, если разрез проведён в см от левого края и в
см от правого края, то длины
полученных кусков нити равны
и
Поскольку этих длин всего две, то
совпадает либо с
либо с
а наименьший кусок
равен
см. Значит,
см или
см, а общая длина нити, равная
тогда может принимать значения
см или
см.
15360 см или 20480 см
Ошибка.
Попробуйте повторить позже
Изначально на табло горит число 0. При нажатии на кнопку число на табло изменяется на 50 или 51. На кнопку нажали 2025 раз. Могло ли после этого на табло гореть число 25, если известно, что на табло не появлялись более чем двузначные числа, а также не появлялись отрицательные числа?
Источники:
Подсказка 1:
В этом процессе нужно найти полуинвариант.
Подсказка 2:
В контексте задачи будет выгодно разделить числа некоторым образом на две группы. Видимо, разделение будет таким, чтобы на каждом шагу было понятно, число из какой группы горит на табло.
Подсказка 3:
Давайте в первую группу возьмём числа от 1 до 49, а во вторую от 50 до 99. Число из какой группы будет после 2025 нажатий?
Первое решение. Назовём числа 0, 1, …, 49 маленькими, а остальные числа, которые могут появиться на табло, т.е. числа 50, 51, …, 99 — большими. Заметим, что после нажатия из маленького числа обязательно получается большое, а из большого числа — маленькое. Значит, после нечётного количества операций на табло будет гореть большое число.
_________________________________________________________________________________________________________________________________________________________________________________
Второе решение. Выстроим все целые числа от 0 до 99 в цепочку
Заметим, что если какое-то число горит на табло, то следующим числом может быть только соседнее число в цепочке. Но так как числа 0 и 25 стоят в цепочке на местах одной чётности, получить из числа 0 число 25 за нечётное количество шагов невозможно.
не могло
Ошибка.
Попробуйте повторить позже
На 2025 островах Северного Ледовитого океана живут несколько медведей. Каждый медведь иногда совершает заплыв,
переплывая с одного острова на другой. Оказалось, что за год каждый медведь совершил хотя бы один заплыв, но никакие
два медведя не сделали поровну заплывов. При этом между каждыми двумя островами и
был совершён ровно
один заплыв: либо из
в
либо из
в
Докажите, что на каком-то острове и в начале, и в конце года не было
медведей.
Источники:
Подсказка 1:
Давайте попробуем обозначить количество медведей через n. С его помощью можно оценить количество заплывов.
Подсказка 2:
Если занумеровать медведей по возрастанию количества их заплывов, то становится ясно, что i-й медведь сделал не менее i заплывов. Отсюда вытекает оценка. А можно ли вычислить количество заплывов в явном виде?
Подсказка 3:
С другой стороны, из условия понятно, что количество заплывов равно количеству пар островов. Сколько их?
Подсказка 4:
Итак, вы получили оценку n ≤ 2024. Используя это, можно некоторым образом оценить, сколько медведей было в начале и в конце года на каждом из островов. А там до окончания решения недалеко.
Подсказка 5:
Каждый медведь в конце и в начале года находится на каком-то острове, поэтому эта величина не больше 4048. Теперь подумайте, как, используя это, найти остров, на котором не было медведей. Быть может, стоит поискать остров, на котором не было медведей либо в начале, либо в конце года?
Подсказка 6:
В этом вам поможет принцип Дирихле. А как насчёт того, чтобы показать, что на таком острове медведей не было на самом деле как в начале, так и в конце года?
Подсказка 7:
Давайте вспомним, что суммарно за год на любом острове ровно происходит 2024 заплыва, которые заканчиваются или начинаются на этом острове. Но если, например, в начале года на острове был 1 медведь, а в конце 0, то может ли количество заплывов быть таким?
Обозначим общее число медведей через Тогда всего заплывов сделано не менее
С другой стороны, общее число заплывов равно количеству пар островов, то есть Таким образом,
откуда
и, следовательно,
Посчитаем, сколько медведей было в начале и в конце года на каждом из островов. В сумме получится не более потому что
каждый медведь в начале и в конце года был на одном из островов. Поскольку
тогда по принципу Дирихле на каком-то острове в начале и в конце года в сумме было не более одного медведя.
Пусть в начале года на медведей не было, а в конце года там был ровно
медведь. Тогда общее число заплывов, заканчивающихся
на острове
на
больше общего числа заплывов, которые на острове
начинаются. Таким образом, остров
был начальной или
конечной точкой для нечётного числа заплывов, но это количество должно равняться
(по одному заплыву в каждую сторону для
каждого из
других островов), что чётно, – противоречие.
Аналогично выясняется, что наоборот тоже не бывает: если в начале года на острове был один медведь, а в конце года – ноль, то
число заплывов, начинающихся на
на
больше числа заплывов, заканчивающихся на
что снова даёт нечётное общее число
заплывов, связанных с
(но
чётно).
Итого на острове и в начале, и в конце года медведей не было, что и требовалось.
Ошибка.
Попробуйте повторить позже
В пространстве даны скрещивающиеся перпендикулярные прямые и
Точки
и
— середины отрезков
и
соответственно. Докажите, что
Источники:
Подсказка 1:
Давайте перенесём EF в левую часть неравенства и будем доказывать в таком формате. Попробуйте ввести некоторые обозначения, чтобы левую часть неравенства можно было записать в более удобном виде.
Подсказка 2:
Деление на 2 намекает, что стоит обозначить через M и N середины AD и BC.
Подсказка 3:
Обратите внимание на четырехугольник MENF. Что про него можно сказать? Не забывайте про перпендикулярность из условия.
Подсказка 4:
MENF — прямоугольник. Используя это, попробуйте превратить левую часть неравенства в сумму звеньев ломаной, которая начинается и заканчивается в BD.
Подсказка 5:
Не забывайте, у прямоугольника диагонали равны.
Обозначим через и
середины отрезков
и
Тогда
— средняя линия в треугольнике
а
— в
треугольнике
Следовательно,
Аналогично
Таким образом, точки
лежат в одной
плоскости, причём из условия
следует, что
— прямоугольник. Значит, равны его диагонали
и
Заметим, что
по неравенству ломаной, остаётся вычесть из обеих частей.
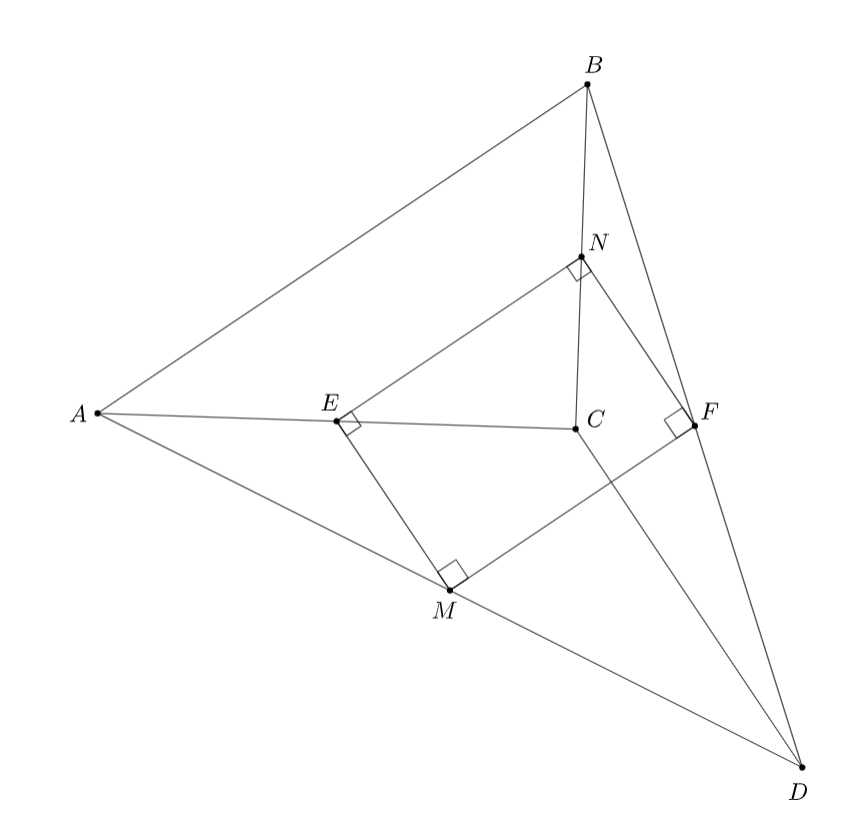
Ошибка.
Попробуйте повторить позже
Саша выбрал 199 многочленов с вещественными коэффициентами так, что сумма любых ста из них имеет вещественный корень. Докажите, что сумма каких-то девяти из них также имеет вещественный корень.
Источники:
Подсказка 1:
По принципу Дирихле найдутся 100 многочленов со старшими коэффициентами одного и того же знака. Пусть это будет плюс. Давайте обозначим их через f₁, f₂, ..., f₁₀₀ и рассмотрим их сумму. Быть может, нам удастся пойти от противного и найти противоречие, связанное с ней?
Подсказка 2:
Давайте предположим, что сумма любых девяти многочленов не имеет корней. Но тогда любая сумма девяти рассмотренных многочленов положительна, не так ли? Как связать эту сумму с суммой всех многочленов?
Подсказка 3:
Давайте рассмотрим суммы вида fᵢ + fᵢ₊₁ + ... + fᵢ₊₈ (будем считать, что fⱼ₊₁₀₀ = fⱼ для всех j). Все они положительные. Что тогда можно сказать про их сумму?
Без ограничения общности можно считать, что многочленов с положительным старшим коэффициентом больше, чем с отрицательным
(иначе домножим все многочлены на ). Тогда можно выбрать 100 многочленов
…,
с положительным старшим
коэффициентом. Рассмотрим многочлены
где и
Получается, что все многочлены
тоже с положительными старшими коэффициентами. Значит,
если они все не имеют корней, то
Но тогда
то есть многочлен
не имеет вещественных корней, противоречие.
Ошибка.
Попробуйте повторить позже
Несколько карточек выложили в ряд слева направо, на каждой карточке написана буква русского алфавита. Назовём набор из 33 карточек
идеальным, если на этих карточках выписаны все буквы в алфавитном порядке слева направо. Известно, что при любом выборе одной буквы
русского алфавита найдутся
идеальных наборов, любые два из которых либо не имеют общих карточек, либо имеют ровно одну
общую карточку, на которой написана буква
При каком наибольшем
в этом ряду гарантированно можно найти
идеальных
наборов, любые два из которых не имеют общих карточек?
Источники:
Подсказка 1:
Попробуйте сначала рассмотреть какие-то примеры ряда и найти наиболее удачный. Подумайте, каким может быть ответ. Возможно, есть смысл ставить большое количество одинаковых букв подряд.
Подсказка 2:
Давайте обозначим буквы через zᵢ и рассмотрим блок букв, в котором сначала 10⁶ раз встречается z₁, потом 10⁶ раз z₂ и так далее до zᵢ₋₁, затем zᵢ встречается один раз, следующие буквы содержатся по 10⁶ раз. Что про такой блок можно сказать?
Подсказка 3:
В нём есть 10⁶ идеальных наборов, у которых zᵢ — общая карточка. А что, если рассмотреть ряд из таких блоков для i = 1, 2, ..., 33? Что можно сказать про него?
Подсказка 4:
Давайте называть карточку, которая встречается в каком-то блоке один раз, особой. Существует ли идеальный набор, не содержащий ни одной особой карточки?
Подсказка 5:
Чтобы это опровергнуть, нужно показать, что найдется такое i, что буква zᵢ встречается в блоке Bᵢ. Кажется, это даст оценку на 33. Осталось показать, что 33 всегда можно выбрать.
Подсказка 6:
Идея доказательства оценки следующая. Давайте через Sᵢ обозначим множество из 10⁶ идеальных наборов, не имеющих общих букв, кроме, возможно, zᵢ. Из каждого такого множества нужно выбрать по набору так, чтобы у них не было общих карточек.
Подсказка 7:
Если в каком-то множестве Sᵢ есть хотя бы 10⁴ наборов с общей карточкой zᵢ, то давайте выкинем из него все остальные, а эту карточку назовём полезной. Попробуйте поочерёдно выбирать по набору из этих множеств так, чтобы набор не содержал полезных карточек других букв и не пересекался с уже выбранными. Обоснуйте, почему получится это сделать.
Подсказка 8:
Пусть выбраны наборы из i - 1 первых множеств, а из i-го не получается. Подумайте, сколько карточек с zᵢ могут содержать выбранные наборы и сколько раз эти карточки встречаются в Sᵢ.
Подсказка 9:
Также обратите внимание на то, что каждая из остальных карточек, содержащихся в выбранных наборах, содержится не более чем в одном наборе из Sᵢ. Какие ещё есть наборы в Sᵢ, помимо тех, которые нельзя выбрать?
Положим Покажем сначала, как выложить карточки так, чтобы больше 33 попарно не пересекающихся идеальных наборов не
нашлось. Для удобства обозначим буквы в алфавитном порядке через
через
будем обозначать последовательность из
карточек, на каждой из которых написана буква
Наш ряд будет состоять из 33 блоков выложенных друг за другом в этом порядке. Блок
выглядит
как:
(единственную карточку с буквой в этом блоке назовём особой). Ясно, что уже в
-м блоке содержится
идеальных наборов, у
которых общей является только особая карточка. Докажем теперь, что в каждом идеальном наборе в полученном ряду есть особая
карточка. Поскольку особых карточек всего 33, отсюда будет следовать, что из любых 34 идеальных наборов два обязательно пересекутся по
какой-то особой карточке, то есть
не может быть больше 33.
Действительно, предположим, что нашёлся идеальный набор, в котором нет особых карточек. Найдётся индекс такой, что буква
этого набора встречается не правее блока
(подходит хотя бы
); выберем наименьшее такое
Если карточка
нашего
набора встречается левее
то
и
также встречается в наборе левее
то есть не правее
это
противоречит минимальности
Значит,
встречается именно в блоке
то есть написана на особой карточке, что и
требовалось.
Осталось показать, что попарно не пересекающихся идеальных наборов выбрать всегда можно. При
обозначим
через
множество из
идеальных наборов, не имеющих общих букв, кроме, возможно,
(оно существует по условию). Мы
выберем из каждого множества по набору так, чтобы в них не было общих карточек.
Для начала, если в каком-то множестве найдутся
наборов, имеющих общую карточку (естественно, с буквой
), выделим
такие
наборов, выбросим из
остальные наборы, а общую карточку назовём полезной для буквы
Теперь мы будем по очереди
выбирать набор из
так, чтобы он не содержал полезных карточек для букв, отличных от
и не пересекался с уже
выбранными наборами.
Пусть наборы из уже выбраны. Если не существует полезной карточки с буквой
то уже выбранные наборы
содержат
карточек с буквой
каждая из которых встречается меньше
раз в наборах в
Выкинув эти наборы,
будем считать, что карточки с
в наборах из
не содержатся в уже выбранных наборах (если полезная карточка с буквой
есть,
это уже выполнено), и в
не меньше
наборов.
Далее, выбранный набор содержит
других карточек, каждая из которых содержится максимум в одном наборе из
выкинув все эти наборы, оставим в
как минимум
наборов, не пересекающихся с уже выбранными. Среди этих наборов максимум
содержат полезные карточки с буквами, отличными от
выбрав любой набор, не содержащий такой карточки, мы завершим
шаг.
После завершения 33-го шага мы получим 33 попарно не пересекающихся идеальных набора, что и требовалось.
При
Ошибка.
Попробуйте повторить позже
График квадратного трехчлена
с вещественными коэффициентами пересекает график
квадратного трехчлена
в точках
и
Касательные в точках
и
к графику
пересекаются в
точке
Оказалось, что точка
лежит на графике
Найдите все возможные значения
Источники:
Подсказка 1
Вычтем из обоих трехчленов линейную функцию, проходящую через A и B. Как теперь выглядят условия задачи?
Подсказка 2
На самом деле, условия касания парабол и прямых, а также пересечение прямых на параболе сохраняются и для новых трехчленов. Осталось решить задачу для более простого случая, когда параболы пересекаются в 2 точках, являющиеся из нулями.
Вычтем из обоих трехчленов линейную функцию, график которой проходит через точки и
Обозначим
полученные трехчлены соответственно
и
(где у
старший коэффициент равен
а у
он равен
). Пусть абсциссы точек
и
равны соответственно
и
Тогда
и
касательные в точках
и
к графику трехчлена
пересекаются на графике
В самом деле,
вычитание линейной функции сохраняет условия касания прямой и параболы в точке с заданной абсциссой, а также
пересечения двух прямых и параболы в одной точке.
Обозначим через
Поскольку
график трехчлена
симметричен
относительно прямой
поэтому касательные к этому графику в точках
и
пересекаются на оси
симметрии. Пусть также точка пересечения касательных имеет координаты
а вершина параболы-графика
имеет координаты
Поскольку старший коэффициент трехчлена равен
имеет место равенство
или
поскольку график
есть парабола
, перенесенная параллельно так, чтобы вершина
попала в
По этой же причине угловые коэффициенты касательных в точках
и
есть
значит,
Таким образом, если перенести параболы-графики
и
так, чтобы
их вершины попали в
то ординаты точек с абсциссой
на этих параболах будут соответственно
и
из чего следует, что старший коэффициент у
в
раза больше, чем у
Ошибка.
Попробуйте повторить позже
У Олега есть набор из 2024 различных клетчатых прямоугольников размеров
…,
(по одному прямоугольнику
каждого размера). Может ли он, выбрав некоторые из них, составить какой-нибудь клетчатый квадрат площадью больше
1?
Источники:
Подсказка 1:
Предположим, что это возможно. Пусть n — наибольшая из длин выбранных прямоугольников. Попробуйте как-нибудь оценить площадь квадрата.
Подсказка 2:
Например, ясно, что его площадь не меньше n², поскольку сторона не меньше n. Возможно, можно найти какое-то противоречие с этим?
Подсказка 3:
Какой может быть наибольшая площадь выбранных прямоугольников?
Предположим противное, и пусть — наибольшая из длин выбранных прямоугольников. Тогда составлен клетчатый квадрат
где
Значит, его площадь не менее
С другой стороны, его площадь не больше, чем суммарная площадь всех
прямоугольников
то есть не больше
Противоречие.
не сможет
Ошибка.
Попробуйте повторить позже
По кругу стоят 100 белых точек. Аня и Боря красят по очереди по одной ещё не покрашенной точке в красный или синий цвет, начинает Аня. Аня хочет, чтобы в итоге оказалось как можно больше пар разноцветных соседних точек, а Боря — чтобы оказалось как можно меньше таких пар. Какое наибольшее число пар разноцветных соседних точек Аня может гарантировать себе независимо от игры Бори?
Источники:
Подсказка 1:
Попробуйте рассмотреть простую стратегию (она будет одинаковой для обоих игроков).
Подсказка 2:
Пусть Аня на каждом ходу ищет пару из неокрашенной и окрашенной точки, красит неокрашенную в противоположный цвет. Сколько пар она сможет создать?
Подсказка 3:
Учтите, что в конце игры количество разноцветных пар должно быть чётным. Почему это так?
Подсказка 4:
Стратегия Бори аналогична. Почему он не позволит Ане создать более 50 пар?
Нужно показать, что Аня всегда может добиться, чтобы разноцветных пар было не меньше 50, а Боря сможет помешать ей добиться, чтобы таких пар было больше 50.
Аня красит в любой цвет любую точку, а дальше каждым ходом выбирает пару из непокрашенной точки и стоящей рядом с ней покрашенной (такая, очевидно, найдётся), и красит непокрашенную точку в цвет, отличный от цвета покрашенной. При этом образуется новая пара соседних разноцветных точек.
Боря каждым своим ходом выбирает пару из непокрашенной точки и стоящей рядом с ней покрашенной, и красит непокрашенную точку в цвет, совпадающий с цветом покрашенной. При этом образуется новая пара соседних одноцветных точек.
Всего в круге имеется 100 пар соседних точек, и каждый игрок делает по 50 ходов. В итоге Боря добьётся того, что хотя бы 50 пар будут одноцветными, а Аня — что хотя бы 49 пар будут разноцветными. Однако количество разноцветных пар всегда чётно. Действительно, после окончания игры пройдём полный круг, начиная с какой-либо отмеченной точки (пусть для определённости с красной). Группы из идущих подряд красных и синих точек будут чередоваться: К—С—К—С—…—К, и значит, встретим пар разноцветных соседей вида К—С столько же, сколько пар вида С—К. Поэтому если пар разноцветных соседних точек не меньше 49, то их хотя бы 50.
50
Ошибка.
Попробуйте повторить позже
Пусть — возрастающая последовательность натуральных чисел. При
обозначим
Какое наибольшее количество натуральных чисел может содержаться среди
…,
?
Источники:
Подсказка 1:
Ясно, что pᵢ от pᵢ₋₁ отличается умножением на (xᵢ - 1) / xᵢ. Попробуйте подобрать такое xᵢ, чтобы pᵢ стало натуральным, если известно, что pᵢ₋₁ — натуральное.
Подсказка 2:
Если взять xᵢ = pᵢ₋₁, знаменатель сократится, и pᵢ будет натуральным.
Подсказка 3:
Отсюда следует вывод, что если некоторое pᵢ натуральное, то все следующие тоже можно сделать натуральными. Осталось понять, при каком минимальном индексе pᵢ может быть натуральным.
Число не может быть натуральным. Если
то
если же
то
— не целое. Следовательно,
натуральными могут быть не более 2023 чисел
Можно взять
тогда
При положим
Тогда
и все будут натуральными.
2023
Ошибка.
Попробуйте повторить позже
На отрезке как на диаметре построена полуокружность и выбрана произвольная точка
на этом отрезке. Девять лучей из точки
делят развернутый угол
на 10 равных частей и пересекают полуокружность в точках
…,
соответственно (в порядке
обхода от
к
). Докажите, что сумма площадей треугольников
и
равна площади четырехугольника
Источники:
Подсказка 1.
Подступиться к площадям из условия сложно, в таких задачах зачастую помогает прибавлять и вычитать области из обеих частей, чтобы получить что-то приятное.
Подсказка 2.
Избавимся от площади четырёхугольника и суммы площадей в одной из частей, сведя всё к равенству двух треугольников.
Подсказка 3.
Требуется доказать, что площади треугольников ZA₂A₈ и ZA₃A₇ равны. Какие формулы могут нам помочь?
Подсказка 4.
Сумма углов при вершине Z равна 180°, поэтому хотим доказать, что ZA₂⋅ZA₈=ZA₃⋅ZA₇.
Подсказка 5.
Надо доказать что-то про произведения отрезков, у каждого из которых один конец лежит на окружности. Это напоминает степени точек.
Подсказка 6.
Отразите картинку относительно XY.
Покажем, что Требуемое в условии равенство получается вычитанием из обеих частей этого равенства площади
серого треугольника с вершиной в точке
а также добавлением площадей двух серых треугольников, примыкающих к хордам
и
(см. рис.).
.png)
Заметим, что
поэтому синусы этих углов равны. Поэтому достаточно доказать, что Покажем, что оба произведения равны
Для этого достаточно доказать следующее вспомогательное утверждение.
_________________________________________________________________________________________________________________________________________________________________________________
Лемма. Пусть и
— две точки на полуокружности с диаметром
точка
лежит на отрезке
и
Тогда
Доказательство. Отметим точку симметричную
относительно
Тогда четырёхугольник
вписан в окружность с
диаметром
Также в силу симметрии
и
то есть точки лежат на одной прямой. Значит,
— точка пересечения диагоналей вписанного четырёхугольника
поэтому
.png)
_________________________________________________________________________________________________________________________________________________________________________________
Таким образом, лемма доказана, что завершает решение задачи.
Ошибка.
Попробуйте повторить позже
Уравнение
имеет положительные решения Докажите, что
Источники:
Обозначим
и перепишем уравнение в виде:
Заметим, что
Дальше, перепишем уравнение в виде
откуда сразу следует, что все его корни строго больше 1. Добавим к каждой части уравнение превратится
в
где
Если обозначить то получим однородное уравнение
из которого следует, что где
Дальше, каждое из уравнений можно переписать в виде
Эти уравнения различны, и каждое из них имеет два различных положительных корня, так как исходное уравнение имеет 4 различных
положительных корня. Из этого следует, что
Так как функция строго убывает при
(это несложно показать, например, взяв производную),
то
Теперь уже легко вычислить и упорядочить :
значит,
Ошибка.
Попробуйте повторить позже
Правильный треугольник со стороной 111 разбит прямыми, параллельными его сторонам, на правильные треугольники со
стороной 1. Все вершины этих треугольников, кроме центра треугольника
отмечены. Назовём множество из нескольких
отмеченных точек линейным, если все эти точки лежат на одной прямой, параллельной стороне
Сколько существует
способов разбить все отмеченные точки на 111 линейных множеств? (Способы, отличающиеся порядком множеств, считаются
одинаковыми.)
Источники:
Рассмотрим равносторонний треугольник со стороной разобьём его на правильные треугольнички со стороной
и отметим
все вершины этих треугольников; полученную конструкцию назовём
-треугольником. В дальнейшем под прямыми мы
всегда будем понимать прямые, параллельные сторонам этого треугольника и проходящие через хотя бы одну отмеченную
точку.
_________________________________________________________________________________________________________________________________________________________________________________
Лемма. Пусть — отмеченная точка в
-треугольнике. Тогда существует единственный способ провести
прямых так, что все
отмеченные точки, кроме, возможно,
покрыты этими прямыми. А именно, для каждой стороны
-треугольника надо провести все
прямые, параллельные ей и лежащие между этой стороной и точкой
включая саму сторону, но исключая прямую, содержащую
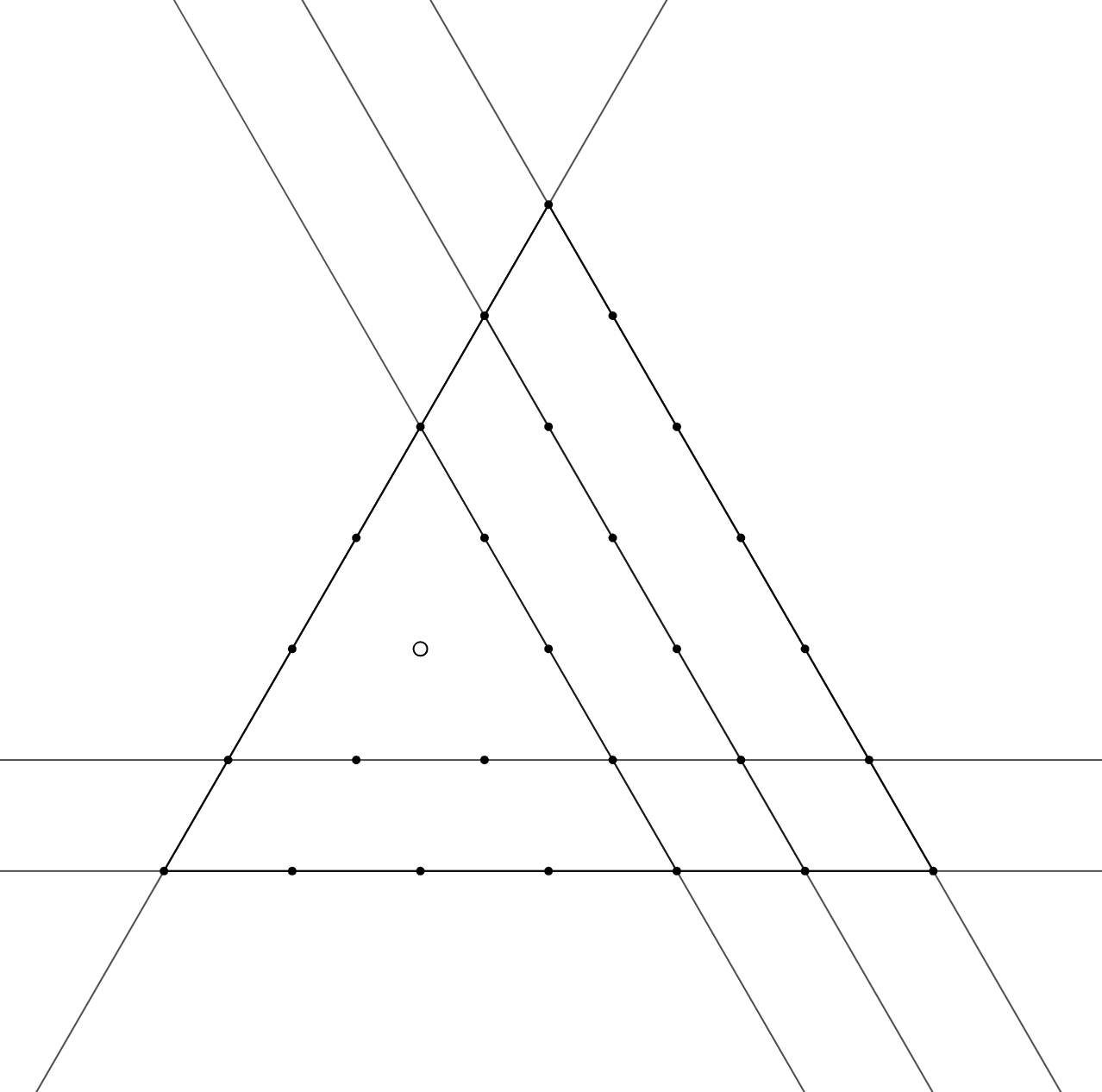
Доказательство. Индукция по База при
проверяется легко: надо провести прямую, содержащую две оставшихся точки,
кроме
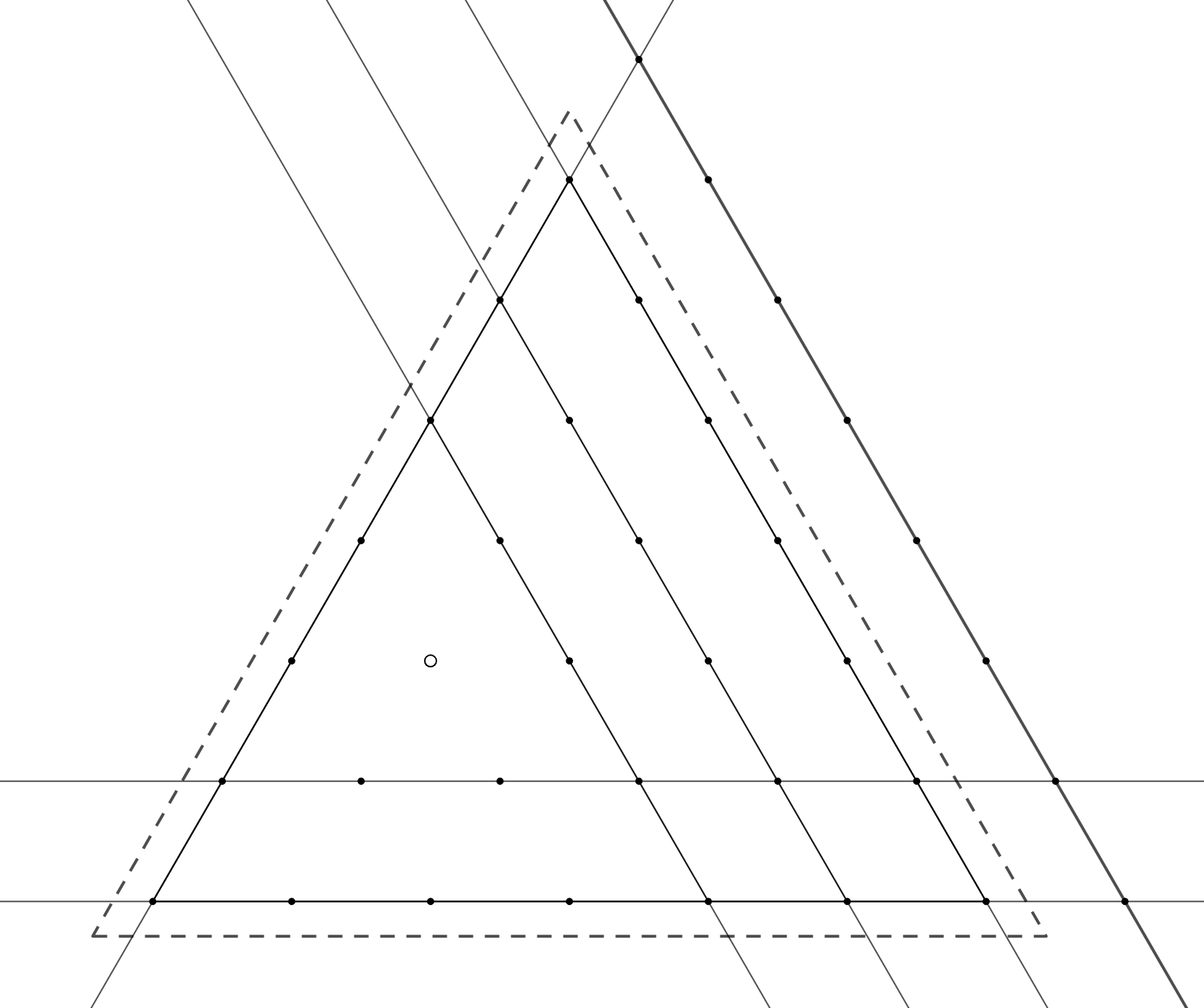
Для перехода рассмотрим сторону -треугольника, на которой не лежит
Если прямая, содержащая эту сторону, не
проведена, то все
отмеченных точек на этой прямой должны быть покрыты различными прямыми; это невозможно,
так как прямых
Значит, эта прямая проведена. Выкинув её и точки
-треугольника, лежащие на ней, получаем
-треугольник, в котором проведено
прямых с теми же условиями. Осталось применять предположение
индукции.
_________________________________________________________________________________________________________________________________________________________________________________
Перейдём к задаче. Рассмотрим одно из разбиений на линейные множества. Для каждого множества проведём прямую, его содержащую.
Тогда эти прямые покрыли все отмеченные точки -треугольника, кроме, возможно, его центра
Значит, эти прямые устроены так, как
описано в лемме, и для любого разбиения этот набор прямых один и тот же.
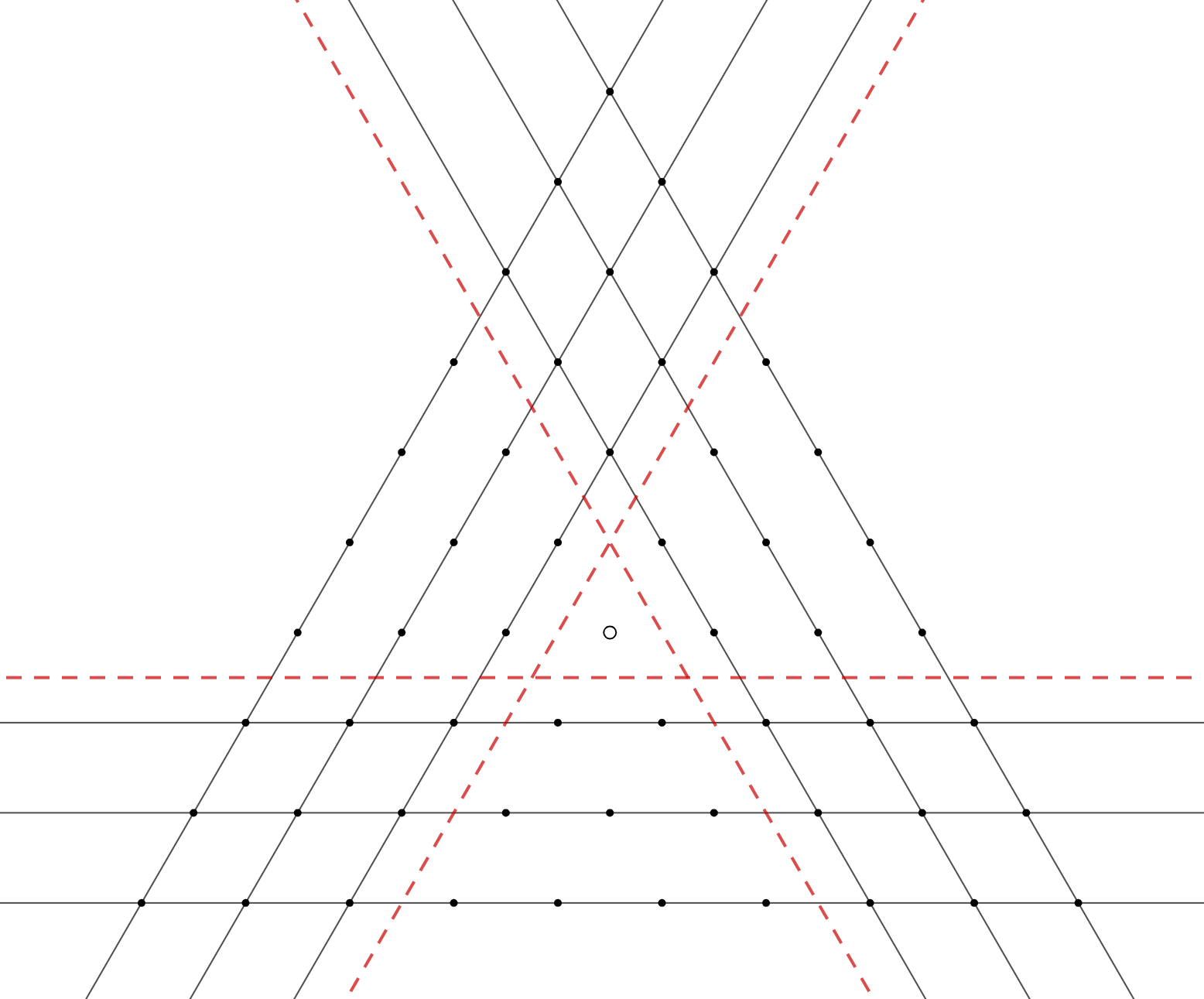
Заметим, что наш -треугольник разбился на
областей: три «ромба» в углах, состоящих из точек, покрытых нашими прямыми
дважды, и три «трапеции» у сторон, в которых каждая точка покрыты одной прямой. Тогда каждая точка в «трапеции» относится к
множеству, лежащему на этой прямой; каждую же точку в «ромбе» можно отнести к любому из двух множеств, лежащих на проходящих
через неё прямых. Все такие выборы можно сделать независимо друг от друга. Поскольку в каждом из трёх «ромбов» всего
точек,
получаем, что требуемых разбиений ровно
Ошибка.
Попробуйте повторить позже
У учителя есть 100 гирь массами 1 г, 2 г, …, 100 г. Он хочет раздать Пете и Васе по 30 гирь так, чтобы выполнялось следующее условие: никакие 11 Петиных гирь не уравновешиваются никакими 12 Васиными гирями, а также никакие 11 Васиных гирь не уравновешиваются никакими 12 Петиными гирями. Сможет ли учитель это сделать?
Источники:
Первое решение. Выберем гирь с массами вида
и дадим Пете, а Васе дадим
гирь с массами вида
г. Тогда масса
любых
гирь, взятых у одного человека, будет делиться на
а масса любых
гирь, взятых у одного человека, не будет делиться на
______________________________________________________________________________________________________________________________________________________
Второе решение. Выберем гирь с массами
и дадим Пете, а Васе дадим
гирь с массами
г.
Тогда у Пети масса любых 11 или 12 гирь будет меньше
г. А масса любых
или
гирь у Васи будет больше
г.
сможет
Ошибка.
Попробуйте повторить позже
В пространстве расположены отрезки
и
с общей серединой
Оказалось, что сфера
описанная около тетраэдра
касается плоскости
в точке
Точка
— центр окружности, описанной около треугольника
Докажите, что
Источники:
Подсказка 1
Каким способом можно доказывать равенство двух отрезков? Может, стоит найти третий отрезок, который будет равен одному из иcходных?
Подсказка 2
Действительно, у нас уже есть пары равных отрезков AM и A'M, BM и B'M, CM и C'M. В частности, это говорит о том, что треугольники ABC и A'B'C' симметричны относительно точки M. Как построить отрезок, равный OM, связь которого со сферой была бы более естественна, чем та же у последнего?
Подсказка 3
Если O' — центр описанной окружности треугольника A'B'C', то OM=M'O. Как эти точки связаны с D?
Подсказка 4
На самом деле, касание сферы и плоскости влечет равенство угла ODO' прямому. Осталось понять, чем является точка M в треугольнике ODO'.
Обозначим через центр окружности, описанной около треугольника
через
— центр сферы
(см. рис.). При центральной
симметрии относительно точки
треугольник
переходит в треугольник
Следовательно, точки
и
симметричны
относительно точки
то есть
— середина отрезка
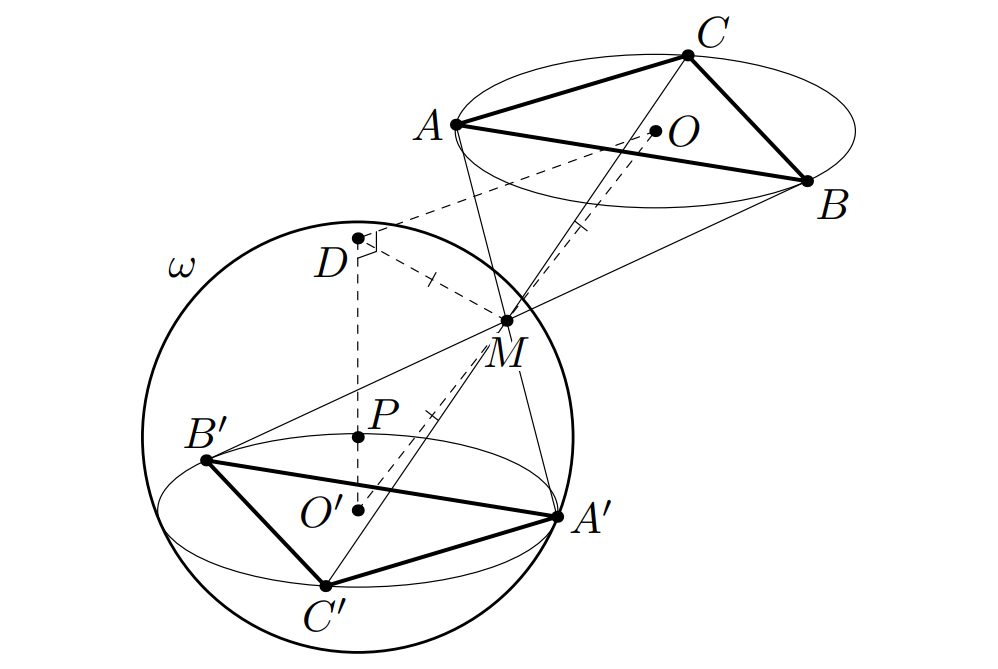
Также мы получаем, что плоскости и
параллельны. Тогда на прямой, проходящей через точку
перпендикулярно этим
плоскостям, лежат точки
и
поэтому
Таким образом,
— медиана в прямоугольном треугольнике
значит,
что и требовалось.



