Стереометрия на устном туре Турнира Городов

Первое решение.

Пусть — центр сферы, а — данный сферический треугольник. По формуле площади сферического треугольника

то есть (Доказательство формулы площади заключается в применении формулы включений-исключений к трём полусферам, пересечением которых является данный треугольник.)

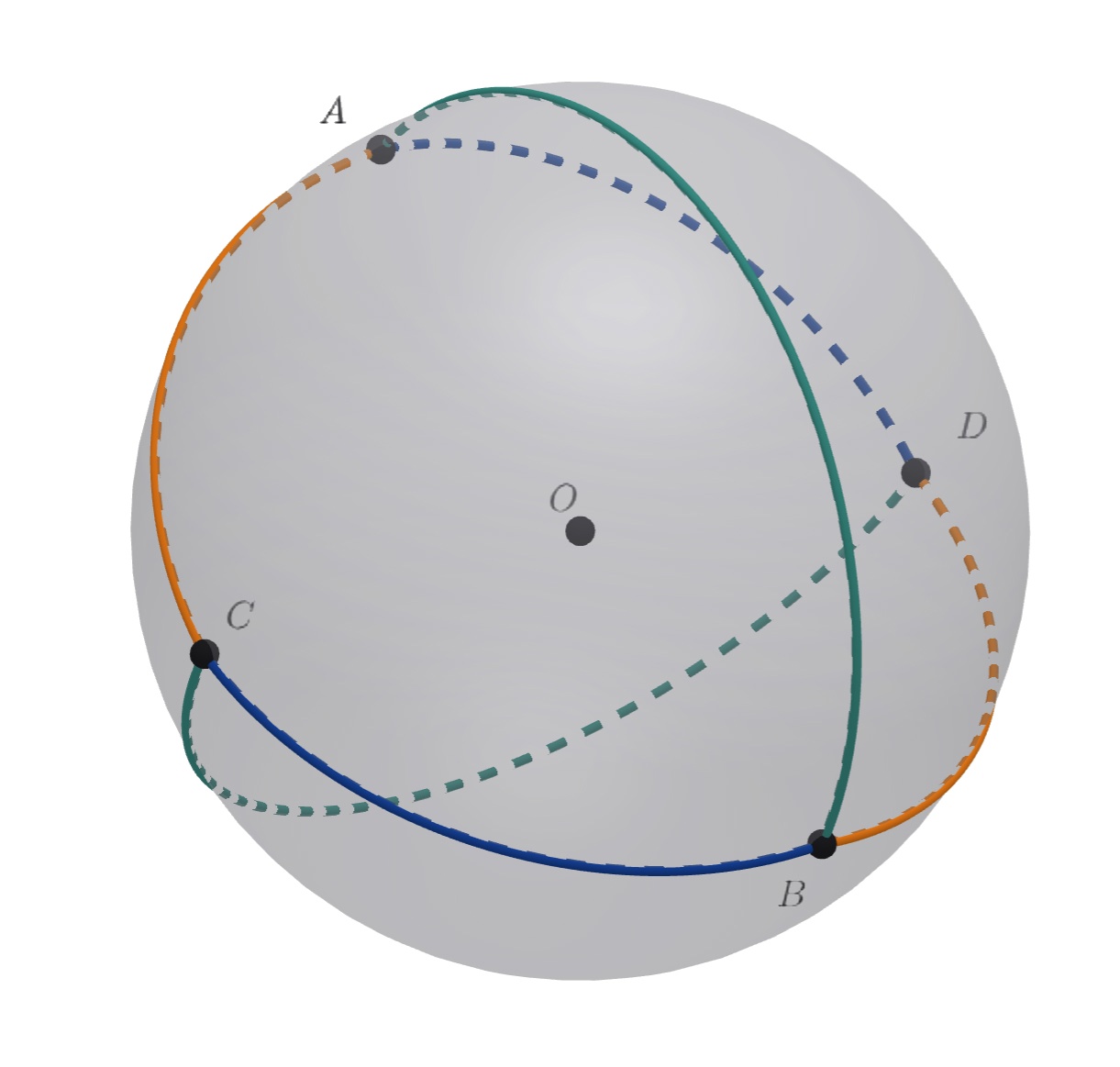
Построим на сфере точку лежащую с в разных полуплоскостях относительно и такую, что и (имеются в виду сферические углы; иначе говоря, точка получена из композицией симметрии относительно и симметрии относительно серединного перпендикуляра к Тогда треугольники и равны. Значит, и Но из условия имеем следовательно, сферические треугольники и также равны треугольнику Четыре полученных треугольника покрывают сферу, так как в сумме без пересечений покрывают поверхность равную площади поверхности всей сферы.

Второе решение.

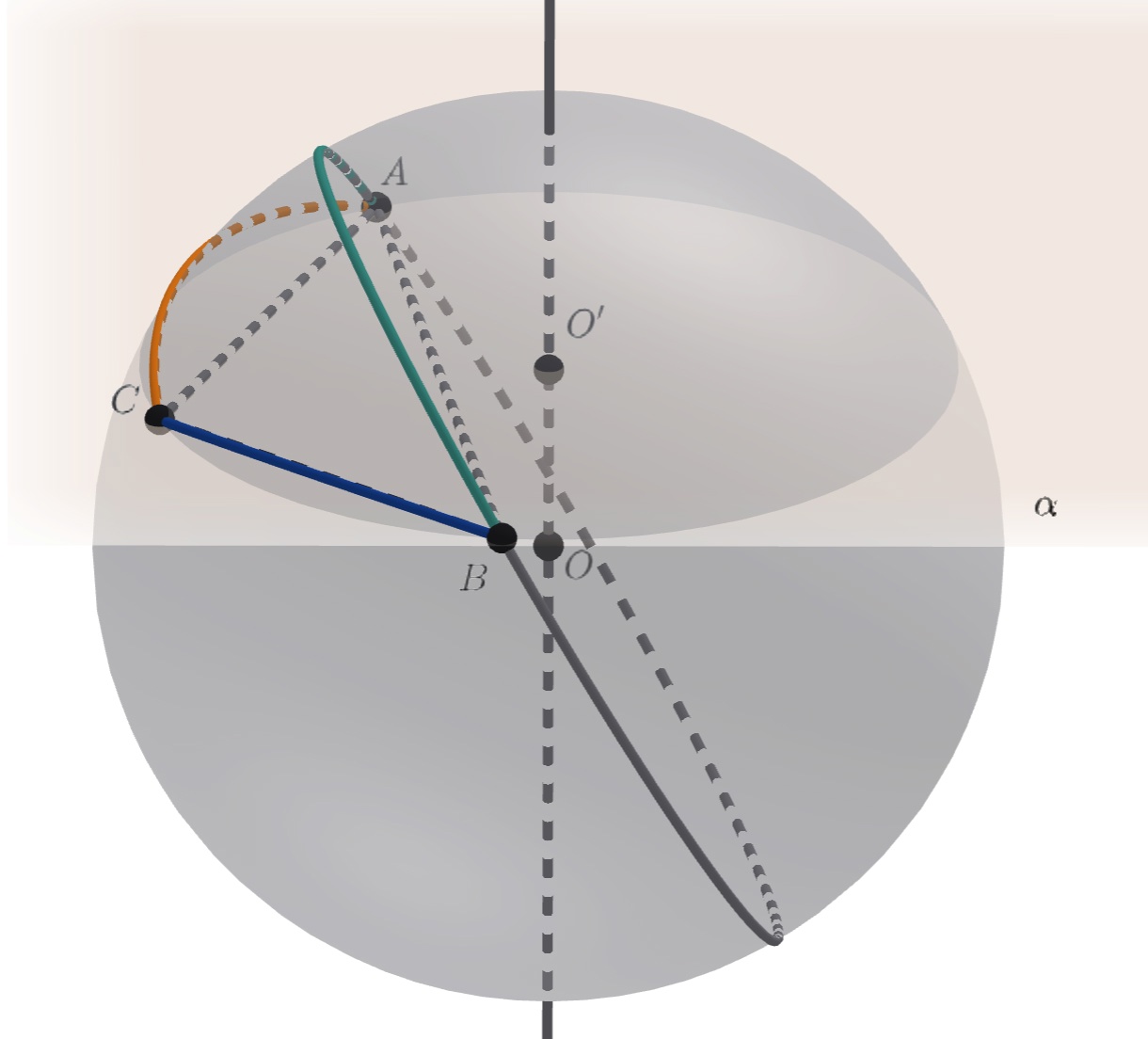
Пусть — вершины данного треугольника. Покажем, что треугольник остроугольный. Действительно, пусть Если плоскость содержит центр сферы, то сферический треугольник вырожден, и его площадь не такая, как надо. Иначе отрезает от сферы «шапочку» площади меньше полусферы. Далее, прямая (нестрого) разделяет и проекцию на значит, часть шапочки, отсекаемая плоскостью и содержащая не больше её половины. Наконец, сферический треугольник лежит в этой области, площадь которой меньше четверти площади сферы — противоречие.

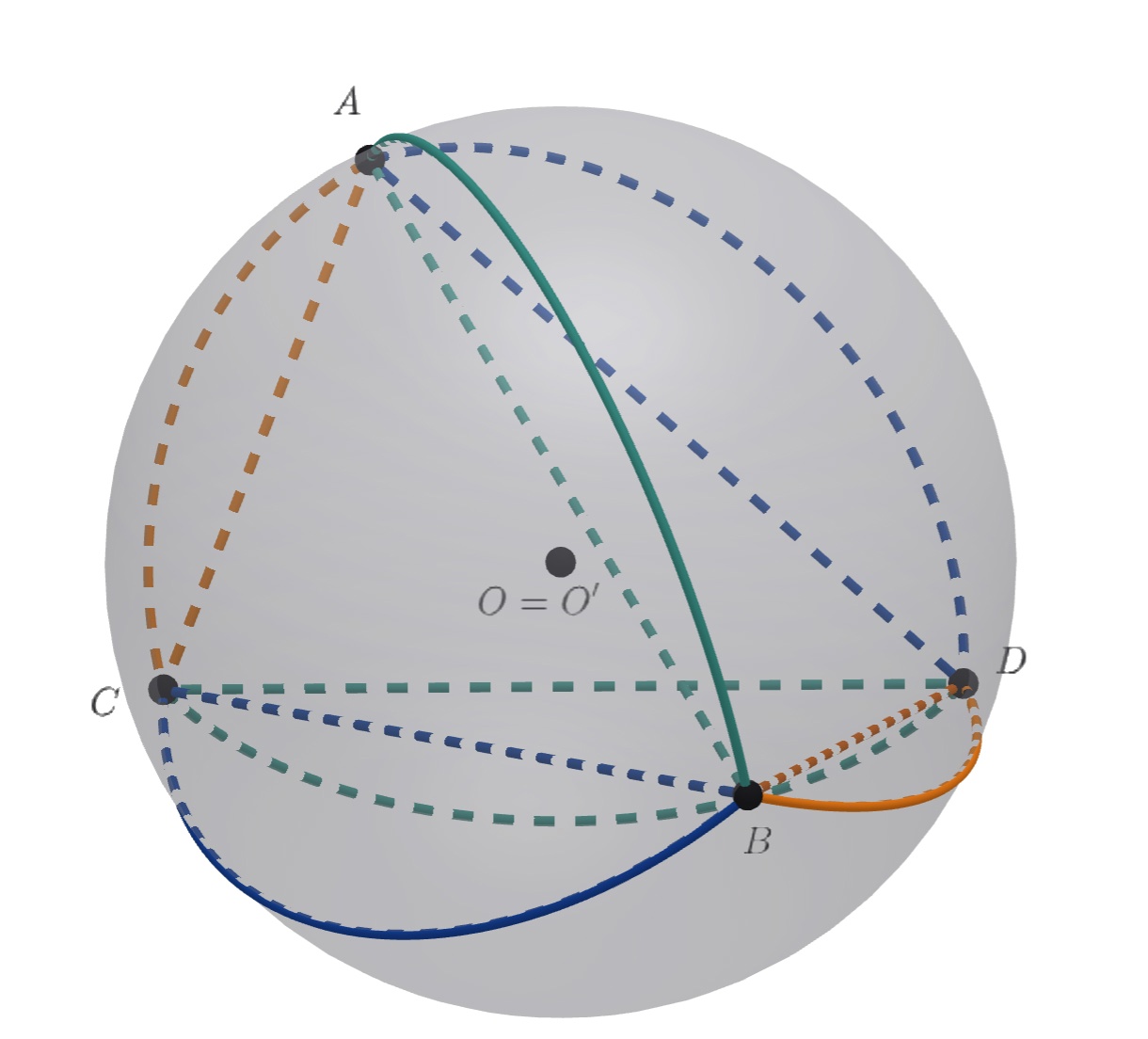
Итак, треугольник остроугольный; тогда существует равногранный тетраэдр (точки и лежат в одной полуплоскости относительно Пусть — центр этого равногранного тетраэдра. Тогда телесные углы разбивают пространство, то есть каждый из них равен четверти площади единичной сферы. Однако, если ближе к чем то этот телесный угол больше, чем а если дальше, то меньше. Оба случая невозможны; значит, и упомянутые телесные углы дают требуемое разбиение сферы на 4 части.