Стереометрия на устном туре Турнира Городов
Ошибка.
Попробуйте повторить позже
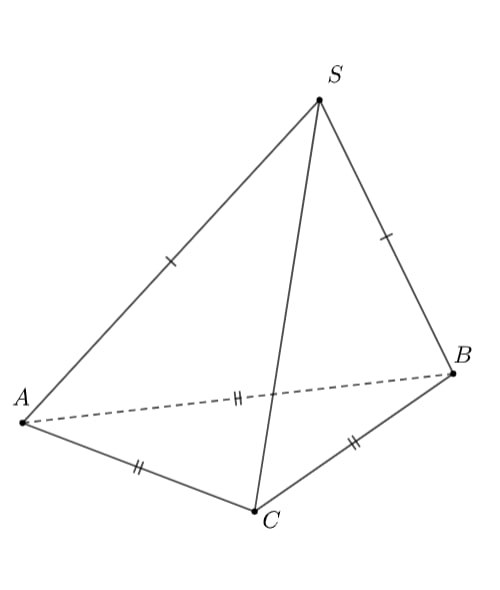
Дана треугольная пирамида , основание которой — равносторонний треугольник
, а все плоские углы при вершине
равны
. При каком наименьшем
можно утверждать, что эта пирамида правильная?
Источники:
Подсказка 1
Эта задача на оценку + пример. Давайте попробуем сначала привести пример для угла, который, как нам кажется, подходит. А потом уже докажем, что для меньшего угла условие задачи не выполняется. Подумайте какой хороший угол нам подойдёт? Слова про правильные фигуры на это всячески намекают.
Подсказка 2
Верно, докажем, что при плоском угле 60 градусов наша пирамида окажется правильной. Нужно только понять, что если в треугольнике есть угол 60 градусов, то сторона напротив него средняя по величине между другими. Тогда предположив, что какое-то боковое ребро не равно ребру из основания, сможем получить противоречие и получить доказательство. Что же будет, если плоские углы будут меньше 60? Попробуйте построить пример неправильной пирамиды с таким углом, учитывая условия задачи и соотношения сторон по их размерам.
Подсказка 3
Давайте, рассмотрим равнобедренный треугольник SAB, в котором SA=SB и ∠S = α(α<60). Тогда сторона AB в нём наименьшая, и мы сможем его отложить на боковых сторонах. Осталось только понять, что отложив на рёбрах трёхгранного угла нужные отрезки(два из которых SA и SB) с плоскими углами меньше 60, мы получим неправильную пирамиду, то есть контрпример.
Докажем, что при пирамида правильная. Пусть стороны треугольника
равны
Заметим, что в любом
треугольнике с углом
против этого угла лежит средняя по длине сторона (причём если она строго меньше одной
из сторон, то строго больше другой). Пусть одно из боковых рёбер пирамиды не равно
например,
Тогда в
гранях
и
рёбра
и
будут меньше
и значит, в грани
ребро
— не средняя сторона,
противоречие.
Покажем теперь, как построить неправильную пирамиду с плоскими углами при вершине
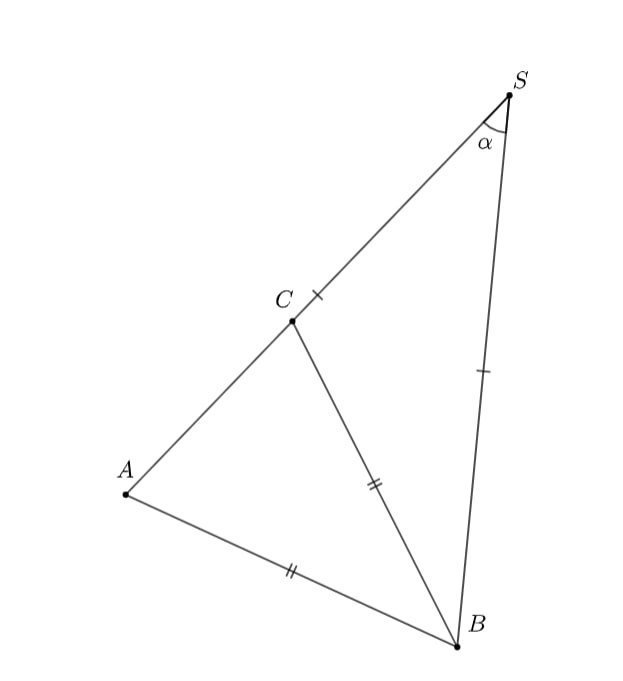
Рассмотрим треугольник c
и
Так как
на стороне
существует такая точка
что
Теперь возьмем трёхгранный угол, у которого все плоские углы равны
и отложим на его ребрах отрезки
Пирамида
— искомая.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




