Планиметрия на ИТМО

Обозначим точку касания вписанной окружности и стороны за Тогда точка лежит на отрезке Это следует, например, из теоремы Брианшона (которая гласит, что главные диагонали описанного шестиугольника пересекаются в одной точке) для вырожденного шестиугольника

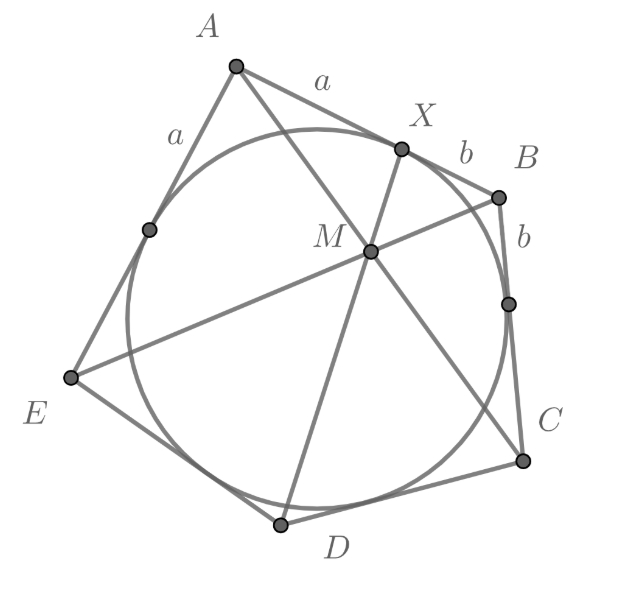
Тогда

поскольку

Обозначим отрезки касания, прилегающие к вершине за , к вершине — за и т.д., а полупериметр пятиугольника за Тогда