Планиметрия на ИТМО
Ошибка.
Попробуйте повторить позже
Дан треугольник 
точка 
— центр его вписанной окружности. На лучах 
и 
соответственно отмечены такие точки (отличные
от 
) 
и 
что 
Докажите, что площади треугольников 
и 
равны.
Источники:
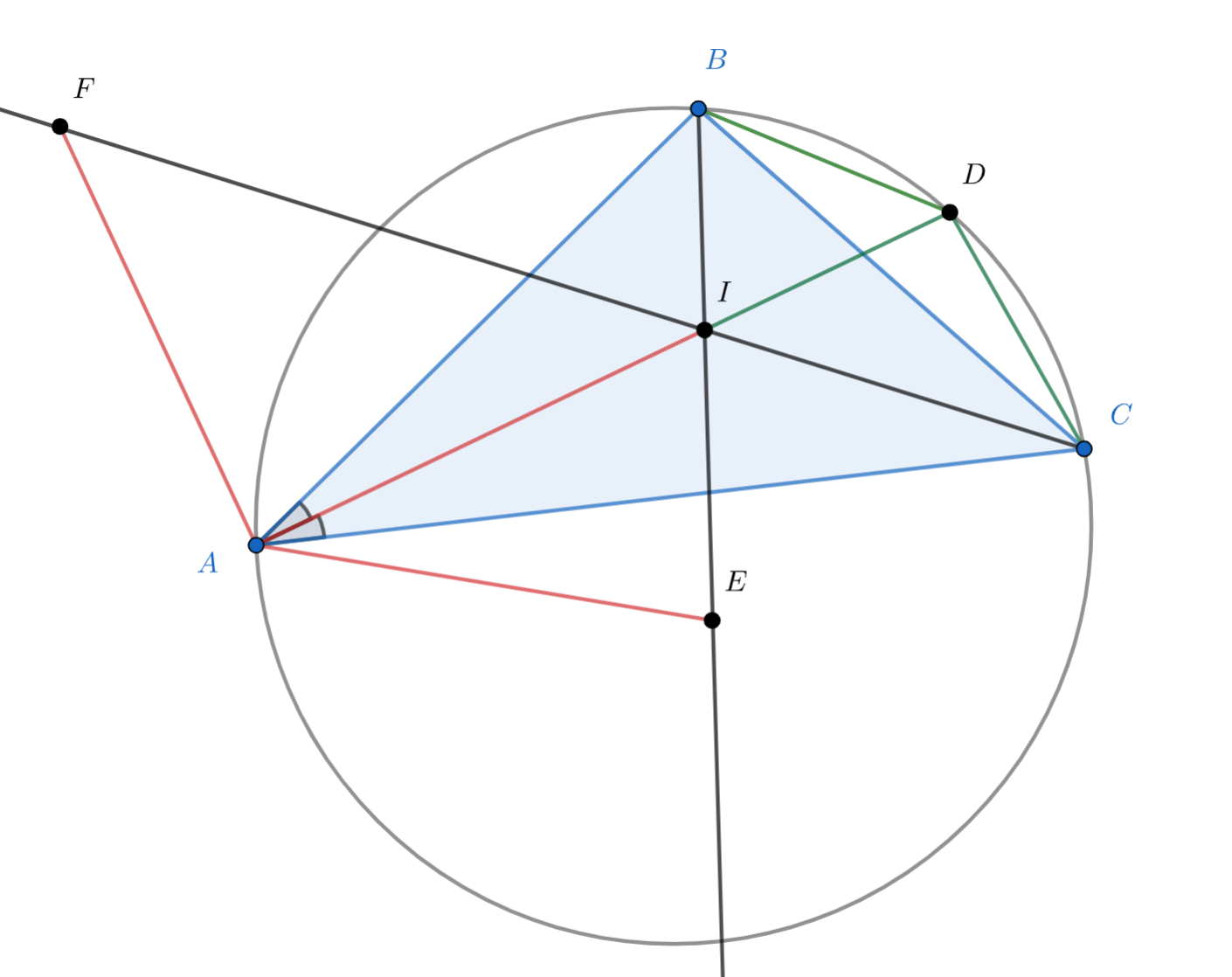
Рассмотрим точку 
— середину дуги 
описанной окружности треугольника 
. По лемме о трезубце 
.
Треугольники 
и 
подобны, так как это равнобедренные треугольники с равными углами при основании (углы в точке 
равны
как вертикальные, потому что точки 
и 
лежат на одной прямой — биссектрисе угла 
). Аналогично подобны треугольники 
и 
.
Отсюда получаем
(первое равенство из первого подобия, второе — из второго). Раскрывая пропорцию, имеем 
. Из этого равенства следует
требуемое равенство площадей треугольников 
и 
, поскольку углы при вершине 
в треугольниках 
и 
равны как
вертикальные.
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
