Планиметрия на ИТМО
Ошибка.
Попробуйте повторить позже
Окружности 
и 
находятся внутри трапеции 
, касаясь друг друга, оснований трапеции, и каждая — своей боковой стороны.
Лучи 
и 
пересекаются в точке 
. Оказалось, что радиус вписанной окружности треугольника 
равен радиусу окружности
и равен 
Также известно, что 
. Найдите площадь треугольника 
Источники:
Радиусы 
и 
равны друг другу и высоте трапеции. Из условия про пересечение лучей следует, что 
— меньшее
основание.
Проведём вторую касательную к вписанной окружности треугольника 
параллельную основаниям трапеции. Обозначим за 
и
точки пересечения этой касательной с отрезками 
и 
— трапеция.
Точки касания окружностей и оснований трапеции образуют квадрат со стороной 
. Если вырезать этот квадрат из трапеции и склеить
оставшиеся части между собой, получится трапеция, равная 
.
Более точно, обозначим точки касания окружностей 
и 
с основаниями трапеции 
: пусть 
и 
лежат на 
(
ближе к 
), 
и 
лежат на 
(
ближе к 
). Кроме того, пусть 
— точки касания вписанной
окружности 
с 
соответственно. Кроме того, пусть 
и 
— точки касания окружностей 
и 
с боковыми сторонами трапеции, 
и 
— центры окружностей 
и вписанной окружности треугольника
.
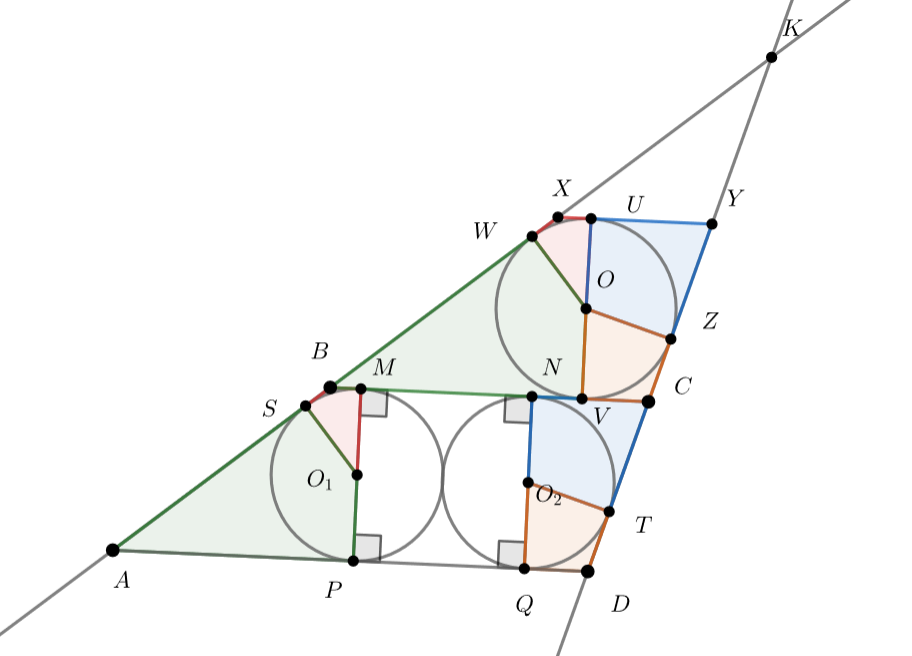
Рассмотрим четырёхугольники 
и 
как соответственные. 
, 
прямые.
Значит оставшиеся углы, 
и 
также равны. Значит, треугольники 
и 
равны. Следовательно,
треугольники 
и 
также равны, а значит четырёхугольники 
и 
равны. Аналогично
Значит,
Пусть 
— длина высоты треугольника 
, проведённой из точки 
. Тогда длина высоты треугольника 
, проведённой из
точки 
равна 
. Значит, коэффициент подобия треугольников 
и 
с одной стороны равен 
, а с другой
, откуда 
. Значит, площадь треугольника 
равна
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
