Планиметрия на ИТМО

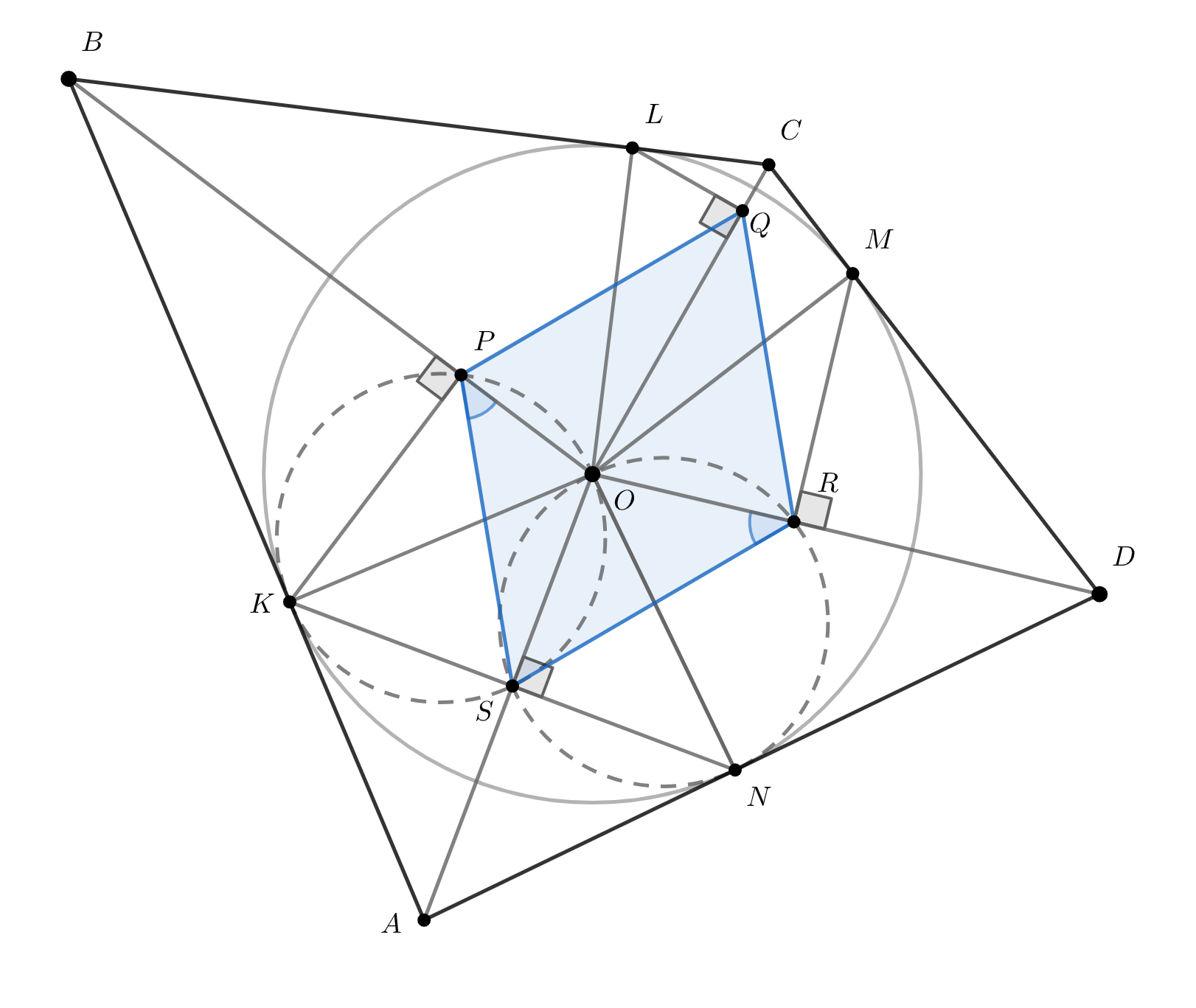
Треугольники и — прямоугольные с общей гипотенузой и катетом, равным радиусу окружности, поэтому они равны. Значит, их высоты падают в одну точку общей гипотенузы, то есть — высота в треугольнике . Поэтому точки и лежат на окружности с диаметром . Аналогично точки и лежат на окружности с диаметром . Поскольку диаметры этих окружностей равны, градусные меры дуги в этих окружностях совпадают. В первой окружности на эту дугу опирается , а во второй - , значит, эти углы равны. (Именно равны, а не дополняют друг друга до , потому что точки и лежат по разные стороны от прямой , а окружности симметричны относительно неё).

Аналогично . Сложив это с предыдущим равенством, получим . Аналогично , то есть четырёхугольник — параллелограмм.

_________________________________________________________________________________________________________________________________________________________________________________

Замечание.

Можно понять, что вершины четырёхугольника инверсны вершинам четырёхугольника относительно нашей окружности, то есть мы только что повторили доказательство теоремы о том, что четырёхугольник, инверсный описанному, является параллелограммом.

_________________________________________________________________________________________________________________________________________________________________________________

Значит, вместо длины отрезка мы можем найти длину отрезка .

По свойству высоты прямоугольного треугольника, . Аналогично , откуда . Кроме того, угол в треугольниках и общий, поэтому они подобны с коэффициентом . Значит,