Стереометрия на ФЕ
Ошибка.
Попробуйте повторить позже
Назовём экономичностъъ многогранника отношение его объёма к площади поверхности. Можно ли разрезать правильный тетраэдр
экономичностью на
частей, сумма экономичностей которых равна
Источники:
Подсказка 1
Хм.. сразу и не угадаешь, но понимаем что разрезание в таких задачах обычно симметрично, подумайте как можно этого добиться.
Подсказка 2
Представьте, что мы отрезаем от тетраэдра одинаковые маленькие тетраэдры. Как изменится объём и площадь поверхности у этих частей по сравнению с исходным телом?
Подсказка 3
Какая фигура останется в центре после отрезания 4 маленьких тетраэдров от вершин? Какие у неё свойства объёма и площади? Остаётся лишь сложить экономичности всех фигур. Что получится в сумме?
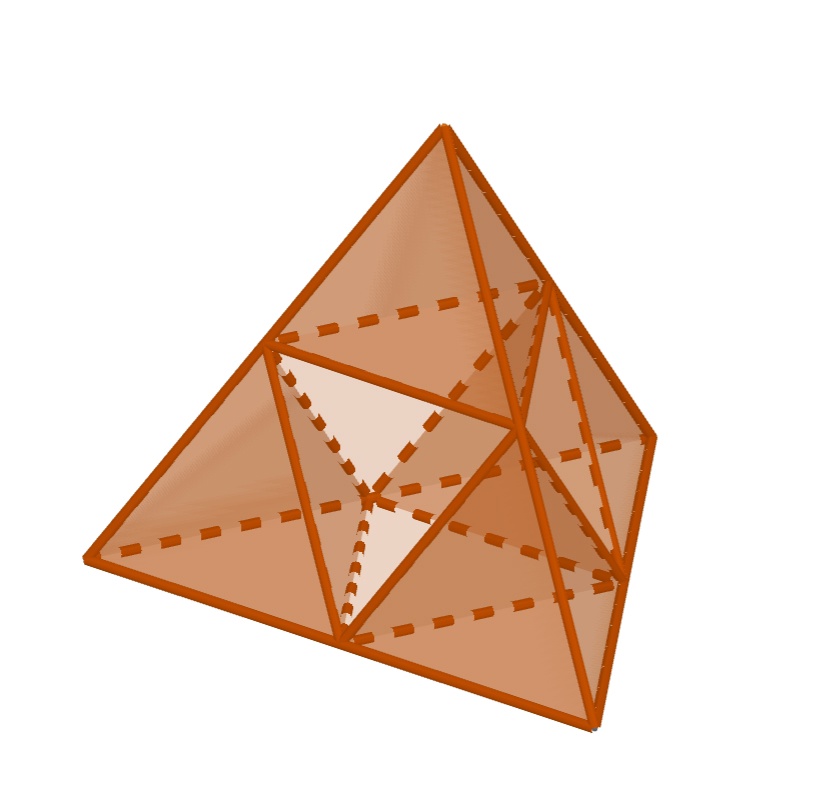
Отрежем от каждой вершины тетраэдра по маленькому тетраэдру с ребром вдвое меньшим, чем у исходного. У каждого
маленького тетраэдра объём в 8 раз меньше, чем у исходного, а площадь поверхности — только в 4 раза, поэтому экономичность
каждого из них равна В середине останется октаэдр, у которого и объём, и площадь поверхности вдвое меньше, чем у
исходного тетраэдра, поэтому его экономичность равна
Действительно, поверхность октаэдра состоит из 8 треугольников, а
исходного тетраэдра — из
таких же треугольников. А объём октаэдра равен
где
— объём
тетраэдра.
Итого сумма экономичностей равна
Да
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




