Системы на Иннополисе
Ошибка.
Попробуйте повторить позже
Дана система уравнений, описывающая положение и ориентацию исполнительного механизма робота на плоскости вида
Найдите конфигурацию ( 
) для заданного положения и ориентации 
, а также известных 
. При каких 
задача имеет решение?
Источники:
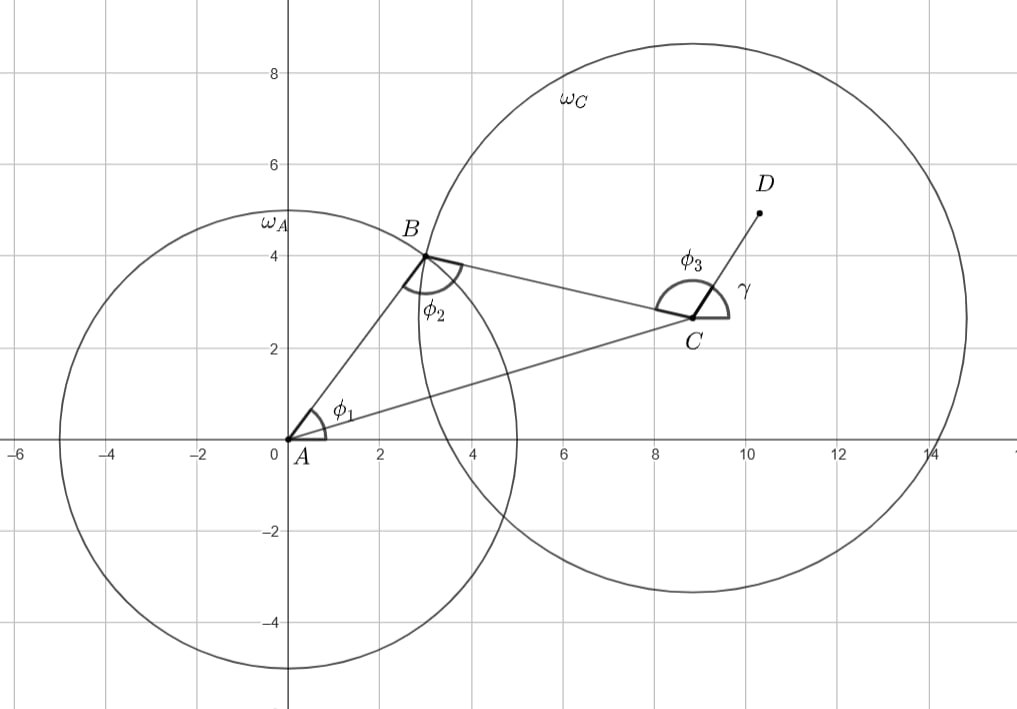
Изобразим на координатной плоскости трехзвенный манипулятор (звенья длин 
, первое звено 
которого — отрезок с началом
в 
, а третье — отрезок с концом 
. Тогда 
— угол, образованный первым звеном и осью 
и 
— углы соответственно
между первым и вторым, и вторым и третьим звеньями манипулятора, а 
— угол между направленным третьим звеном и положительным
направлением оси 
Изобразим окружности 
и 
с центрами в точках 
и 
и радиусами 
и 
соответственно. Вектор 
(третье звено
манигулятора) образует известный угол 
— таким образом, точка 
имеет координаты 
. Изобразим окружность
с центром в точке 
и радиусом 
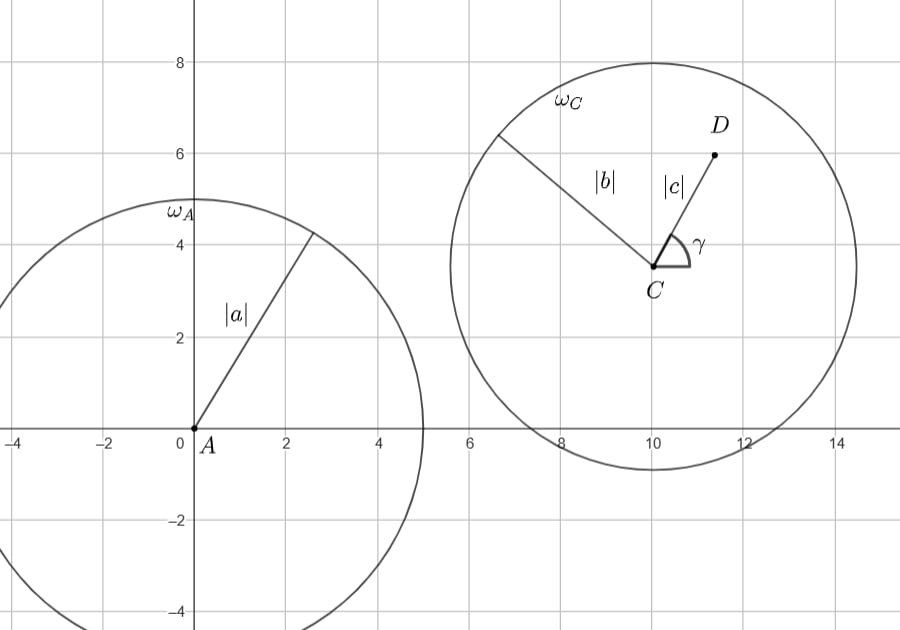
Количество общих точек окружностей 
и 
равно количеству решений задачи. Задача не имеет решений, если треугольника (пусть
и вырожденного) со сторонами 
не существует.
Найдем одно из решений задачи. Рассмотрим 
— второе звено манипулятора). В нём
Зная стороны треугольника, найдем его углы (используя теоремы синусов и косинусов). Так,
причём
Аналогично,
Наконец, 
Задача имеет решение, когда существует треугольник с длинами сторон 
, 
и 
.
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
