Формула Эйлера для графов и многогранников

Рассмотрим нарисованные окружности как плоский мультиграф (граф с кратными ребрами между вершинами): вершины – точки пересечений, ребра – дуги нарисованных окружностей, ограниченные точками пересечений. В такой интерпретации круглосторонники — это все грани этого графа, кроме «внешней» (т.е. части плоскости, лежащей вне всех окружностей).

Пусть нарисованы ровно окружностей. Согласно формуле Эйлера для плоских графов,

где — число вершин графа, — число ребер, а — – число граней (включая внешнюю).

Так как каждая пара окружностей пересекается ровно в двух своих уникальных точках, то число вершин

Так как каждая вершина – это точка пересечения ровно двух окружностей, то наш граф является регулярным степени (то есть в каждую вершину входят ровно ребра). Поскольку каждое ребро соединяет две вершины, общее число ребер

Следовательно число граней нашего плоского мультиграфа должно быть равно

Значит, число круглосторонников

Найти наименьшее такое, что — значит найти наименьшее натуральное решение неравенства

Решив, получаем, что наименьшее равно соответственно

Теперь заметим, что для любого (в том числе для можно расположить окружностей на плоскости так, что каждая пара пересекается ровно в двух своих уникальных точках. Действительно, нарисуем произвольную окружность на плоскости и выберем произвольную точку внутри нее (но не являющуюся ее центром), а потом рассмотрим окружностей где которые получаются в результате поворота окружности вокруг точки на угол (окружность совпадает с На рисунке приведен пример для

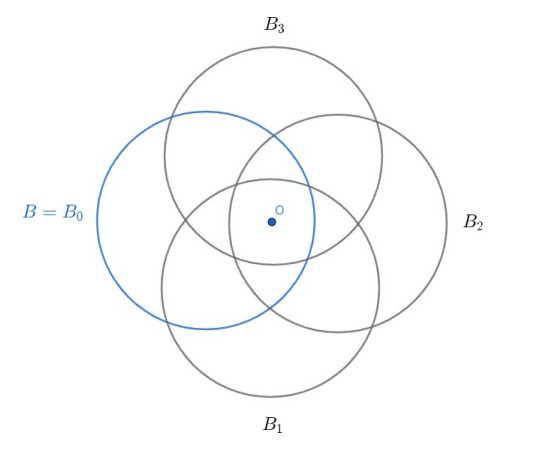
Теперь докажем, что обязательно найдется круглосторонник, ограниченный менее чем дугами. Предположим, что все круглосторонники ограничены не менее чем дугами. Тогда общее число «сторон» (дуг, ограничивающих круглосторонники) не меньше, чем Пусть — число границ внешней грани плоского мультиграфа, тогда

Это невозможно, — следовательно, неверно предположение, что все круглосторонники ограничены не менее чем дугами. Поэтому обязательно найдется круглосторонник, ограниченный менее чем дугами, что и требовалось доказать.