Планиметрия на ШВБ
Ошибка.
Попробуйте повторить позже
Окружность проходит через вершины и
равнобедренного треугольника
и пересекает стороны
и
в точках
и
соответственно.
хорда этой окружности, равная по длине
содержит точку
лежащую на
и являющуюся основанием высоты треугольника
Прямая, проходящая через точку
и
перпендикулярная
пересекает прямую
в точке
Найти радиус окружности, описанной около треугольника
если
Источники:
Подсказка 1
Что можно сказать о четырёхугольнике AMNC?
Подсказка 2
AMNC — равнобокая трапеция! Было бы полезно найти окружность, на которой лежать точки K, M, L. Например, найти вписанный четырёхугольник, вершинами которого являются эти точки. Какие есть подозрения на четвёртую вершину?
Подсказка 3
Давайте попробуем доказать, что BMKL — вписанный! Равенство каких углов нам для этого нужно?
Подсказка 4
Попробуем доказать, что углы MBK и MLK равны! Очень часто помогает идея разбить нужные углы на части, а затем доказать попарное равенство частей.
Подсказка 5
Что можно сказать о треугольниках CBH и NLC?
Подсказка 6
Треугольники CBH и NLC подобны! Тогда можно будет выписать соответствующие отношения сторон и попробовать найти другие подобные треугольники!
Подсказка 7
Рассмотрите треугольники KCL и BHK. Можно можно сказать про отношение их сторон? А о тупых углах в них?
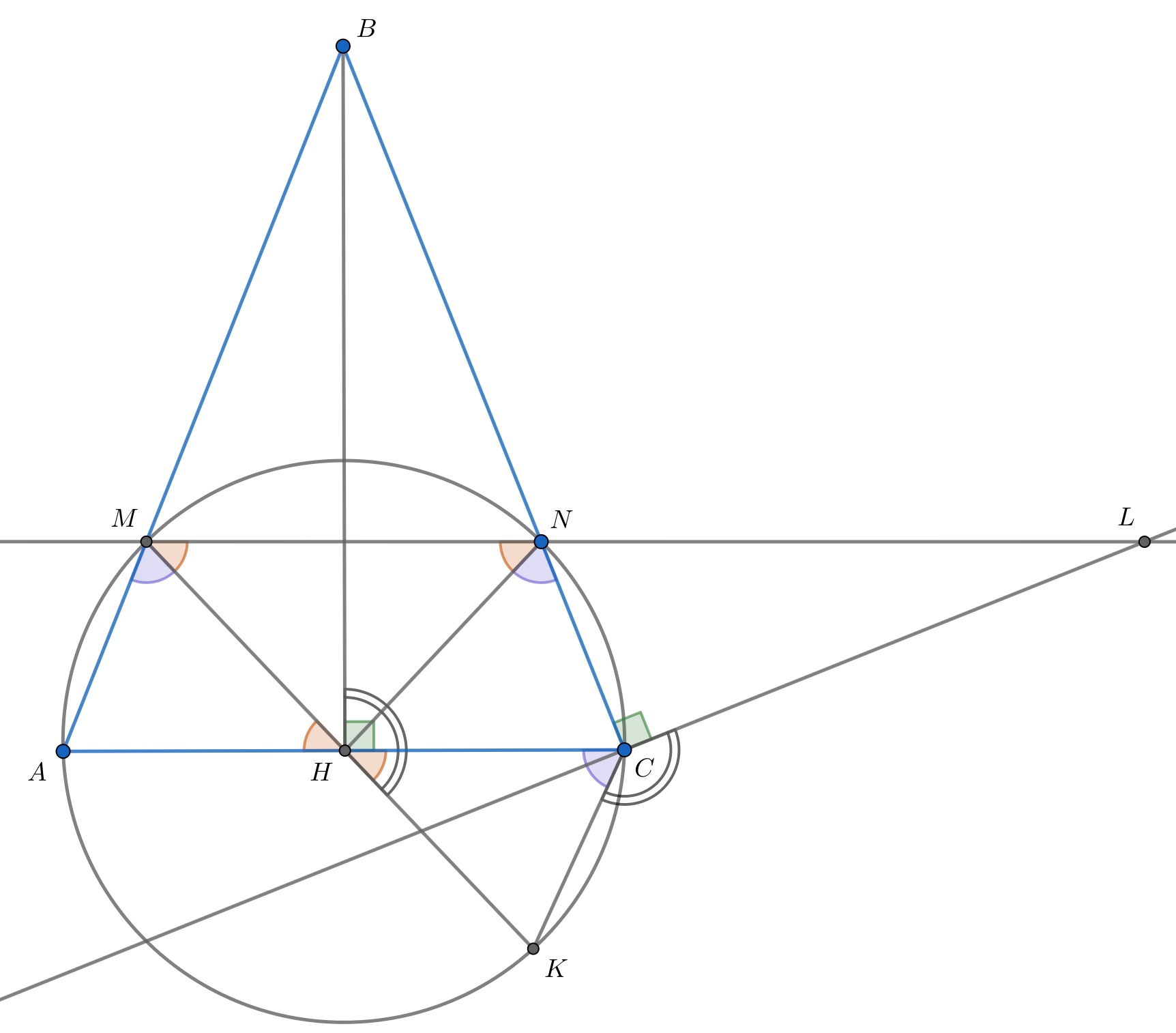
Четырехугольник — равнобедренная трапеция. Треугольники
и
равны по двум сторонам и углу между ними.
Тогда:
(как углы равных треугольников и как углы, опирающиеся на одну дугу). Следовательно, треугольник подобен треугольнику
и треугольник
подобен треугольнику
по двум углам. Значит,
и учитывая, что , получаем подобие треугольника
и треугольника
следовательно,
а значит, точки лежат на одной окружности и
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




