Планиметрия на ШВБ
Ошибка.
Попробуйте повторить позже
Высота треугольника
является диаметром окружности, которая пересекает стороны
и
в точках
и
соответственно. Прямые, касающиеся этой окружности в точках
и
пересекаются в точке
Прямая
пересекает сторону
в точке
Найдите отношение
:
и длины отрезков
и
если
Источники:
Подсказка 1
Что нам дает тот факт, что BH — диаметр окружности? Как это использовать при нахождении длин новых отрезков?
Подсказка 2
Все углы, опирающиеся на BH в нашей окружности — прямые! Тогда на картинке немало подобных треугольников, а также есть касательные, про которые мы также знаем полезные свойства для нахождения длины. Используя это, нам не составит труда найти стороны треугольник ABC.
Подсказка 3
Точка F пока что "витает в воздухе". Что хочется провести, чтобы иметь возможность "перенести" отношение AK : KC?
Подсказка 4
Проведите через F прямую, параллельную AC. Тогда можно будет посчитать углы и найти, например, равнобедренные треугольники!
Найдем стороны треугольника Треугольники
и
подобны, откуда:
Подставим и получаем квадратное уравнение относительно
Треугольники и
подобны:
Аналогично подставим и решим уравнение:
Тогда из теоремы Пифагора для прямоугольных треугольников найдем катеты:
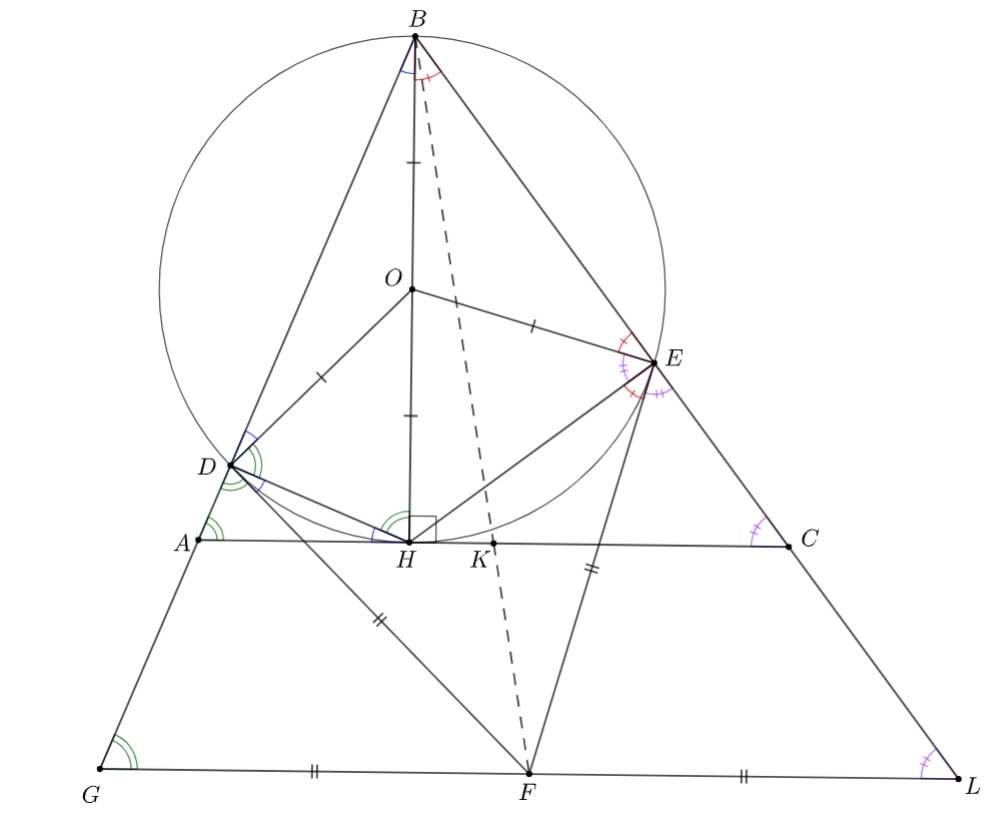
Найдем отношение Проведем через
прямую параллельную
обозначим точки пересечения продолжения сторон
и данной прямой
Пусть
— центр окружности. Тогда:
Треугольник равнобедренный,
Аналогично, треугольник
равнобедренный,
По свойству
касательных
поэтому
Следовательно,
— медиана треугольника
Треугольники
и
подобны,
— медиана треугольника
Таким образом:
Найдем длину Медиана треугольника
по формуле длины медианы:
Найдем длину
По теореме косинусов:
Тогда:
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




