Планиметрия на ШВБ
Ошибка.
Попробуйте повторить позже
В треугольник со сторонами
,
вписана окружность с центром в точке
, которая касается сторон
и
в точках
и
соответственно. На прямой
отмечена точка
так, что угол
равен
. Найдите длину отрезка
.
Подсказка 1
Во-первых, давайте поймём, что у нас за картинка. А картинка у нас фиксирована, то есть мы можем вычислить (возможно, с большой сердечной болью) любой объект на картинке. А значит, скорее всего, задача на счёт. При этом, если мы уже хотим считать, то давайте посчитаем углы треугольника (возможно, угол OAK равен 60 градусам неспроста, иначе, непонятно как связать его хоть с чем-то)
Подсказка 2
По теореме косинусов угол ABC равен 60 градусам. Значит, угол AOC — 120. То есть, прямые OC и AK параллельны, а где параллельность — там и подобие.
Подсказка 4
Мы знаем KM, а значит, так как знаем KM и MT, то знаем и KN.
Заметим сразу, что , то есть треугольник
— остроугольный. А значит,
и
. Поэтому
точка
лежит снаружи треугольника
Обозначим углы треугольника за По теореме косинусов найдем угол
Проведем . Тогда
Поэтому, так как
по условию,
Пусть — точка пересечения
и
.
— биссектриса, медиана и высота в равнобедренном треугольнике
, поэтому
![]()
Тогда из прямоугольного треугольника получаем
По теореме косинусов найдем угол
По формуле половинного угла
По основному тригонометрическому тождеству
И тогда
А из треугольника находим
В итоге
Ошибка.
Попробуйте повторить позже
Биссектрисы внешних углов треугольника
пересекают продолжения противоположных сторон треугольника в
точках
соответственно. Найдите угол
и длину отрезка
если
а угол
равен
Подсказка 1
Мы знаем, что биссектрисы в треугольнике пересекаются в одной точке. Попробуйте провести аналогичное доказательство к тому, что эти три точки на самом деле лежат на одной прямой)
Подсказка 2
Для этого попробуйте также записать всякие отношения и теорему Менелая!
Подсказка 3
Мы поняли, что эти три точки на одной прямой, а значит искомый угол = 180 градусов. Теперь давайте перейдем к отрезку A₁B₁. Для начала можно поискать все что можно в треугольнике ABC, например, недостающую третью сторону)
Подсказка 4
Да, это можно сделать с помощью теоремы косинусов! А теперь попробуйте опять же записать множество отношений и некоторые отрезки представить в виде суммы отрезков. С этой технической работой можно дойти до нужного отрезка!
Обозначим
Треугольники и
имеют общую высоту из общей вершины
следовательно, можем записать следующие соотношения
для их площадей
| (1) |
Пусть — перпендикуляр из
к прямой
— перпендикуляр из
к прямой
Так как
—
биссектриса
значит, точка
равноудалена от прямых
и
Следовательно,
Благодаря этому
получаем
| (2) |
Из соотношений (1) и (2) следует, что
Аналогично получаем
Тогда
Значит, по теореме Менелая точки лежат на одной прямой. Т.е.
и
![]()
По теореме косинусов найдём
Теперь найдём
Аналогично получаем и
Обозначим
Получим значения
и
из двух теорем
косинусов
Запишем теорему косинусов в
Углы и
равны как вертикальные. Запишем теорему косинусов в
Следовательно,
Ошибка.
Попробуйте повторить позже
В выпуклом четырехугольнике длины сторон
и
равны,
— биссектриса угла
Найдите
косинус угла
если
— точка пересечения диагоналей
и
и
Источники:
Подсказка 1
Сразу запишем все отрезки через переменные, пользуясь свойством биссектрисы) Как воспользоваться тем, что у четырехугольника есть две равные стороны? Не забываем, что диагональ DB является биссектрисой!
Подсказка 3
Произведение отрезков диагонали равны! Запишем это, и, т.к. у нас все отрезки теперь выражены с помощью двух переменных, сможем применить теорему косинусов, чтобы избавиться от одной переменной) Осталось лишь понять, как искать косинус нужного угла, если мы знаем отношения практически всех отрезков на картинке!
пусть
пусть
— биссектриса треугольника
Точка является точкой пересечения серединного перпендикуляра к диагонали
и биссектрисы угла
в выпуклом
четырехугольнике
Следовательно, около этого четырехугольника можно описать окружность.
Действительно, опишем окружность около треугольника обозначим точку пересечения биссектрисы угла
с окружностью через
Тогда по свойству вписанных углов дуги
и
будут равны, хорды
и
тоже будут равны, треугольник
будет равнобедренным, и серединный перпендикуляр к диагонали
и биссектриса угла
будут пересекаться в точке
Следовательно,
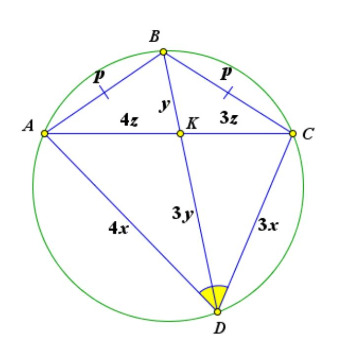
Поскольку около четырехугольника можно описать окружность, то для его диагоналей верно равенство
Треугольник подобен
, и
, пусть
поэтому
По теореме косинусов для треугольников и
с учетом
имеем
Для равнобедренного треугольника имеем



