Тема ШВБ (Шаг в будущее)

Стереометрия на ШВБ

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела швб (шаг в будущее)

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#86474

Основанием четырехугольной пирамиды $SABCD$ является параллелограмм $ABCD$ со сторонами $AB =2√3,AD = 4√3$ и углом $A$ , равным $∘ 60$ . Высотой пирамиды $SABCD$ является отрезок $SO$ , где $O$ - точка пересечения диагоналей параллелограмма $ABCD, SO = 1$ . Найдите площадь сечения пирамиды $SABCD$ плоскостью, параллельной медиане $SE$ боковой грани $SAB$ и проходящей через середину ребра $SC$ и середину отрезка $AO$ .

Источники: ШВБ - 2024, 11.5 (см. olymp.bmstu.ru)

Подсказки к задаче

Подсказка 1

То, что в условии нам даны все длины, может подтолкнуть к тому, что это очень техническая задача. Здесь придется много считать и не бояться больших и страшных дробей. Первым делом нужно построить сечение. Поищите точку, принадлежащую сечению, на плоскости ABCD.

Подсказка 2

Теперь рассмотрим саму плоскость ABCD. У нас есть прямая, лежащая в этой плоскости и принадлежащая сечению. Где эта прямая пересекает прямые, содержащие стороны параллелограмма ABCD? Найдите отношения с помощью теоремы Менелая и подобия.

Подсказка 3

Пусть эта прямая пересекает прямые AB,BC,CD, AD в точках F,G,H,I соответственно. Пусть L - точка, в которой прямая HM пересекает ребро SD. Тогда искомое сечение это LMGI. Найдем его площадь как разность площадей треугольников LHI и MGH. А как найти их площади? Много считать длины сторон и отношения, используя теоремы Менелая, Герона, Пифагора, косинусов.

Показать ответ и решение

Пусть $M$ — середина ребра $SC,$ а точка $K$ - середина отрезка $AO$ . Рассмотрим плоскость $(CSE)$ . Так как плоскость сечения параллельна медиане $SE$ и проходит через точку $M$ , построим прямую $MT ||SE$ в плоскости $(CSE )$ . Тогда $MT$ - средняя линия в $CSE$ , а $T$ середина $CE$ .

Теперь нам известны три точки сечения: $T,M, K$ . Рассмотрим основание пирамиды $ABCD$ и посмотрим, как прямая $TK$ пересекает стороны основания. Пусть эта прямая пересекает прямые $AB,BC,CD, AD$ в точках $F,G,H,I$ .

$PIC$

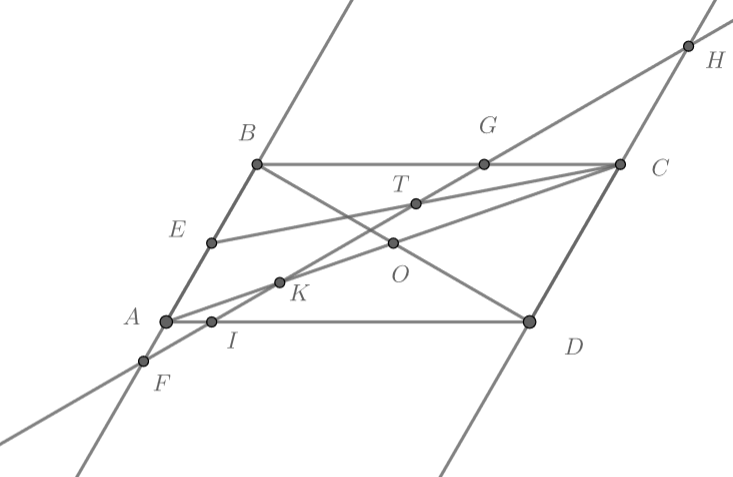
Из теоремы Менелая для треугольника $ACE$ получаем, что

EF-= CK-⋅ TE-= 3 FA AK CT 1

Так как $EA = 1AB 2$ , то $FA = 1AB 4$ .

Далее замечаем, что $△F AK ∼ △HCK$ . Тогда

AF- AK- 1 HC = CK = 3

Откуда $3 HC =3AF = 4AB$ .

Из подобия $△FAI ∼△HDI$ получаем

AI AF 1 ID-= DH-= 7

То есть $AI = 18AD$ .

Аналогично из подобия $△FBG ∼ △HCG$ получаем

BG-= FB-= 5 GC CH 3

То есть $BG = 58BC$ .

Проведем $GG ′||CD$ , где $G′$ - точка на $AD$ . Тогда

GG ′ =AD = 2√3;G′I =AD − 3BC − 1BC = BC-= 2√3 8 8 2

И $∠GG ′I =180∘− ∠A= 120∘$ . Тогда из теоремы косинусов для треугольника $GG ′I$ получим $IG = 6$ .

$PIC$

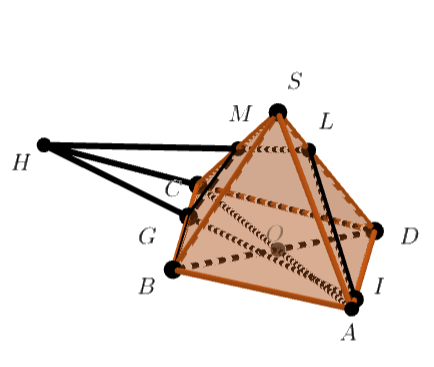
Пусть $L$ - точка, в которой прямая $HM$ пересекает ребро $SD$ . Тогда из теоремы Менелая для $△CSD$ и прямой $HM$ получим:

7 DL-= CM- ⋅ DH =1⋅-4CD = 7 SL SM CH 34CD 3

Далее из теоремы Менелая для $△DHL$ имеем:

HM CH SD 5 ML--= DC-⋅-SL = 2.

В силу параллельности прямых $BC$ и $AD$ имеем $HHGI-= 37$ , откуда $HG = 92,HI = 212$ . По теореме косинусов для $△ABD$ имеем $BD = 6$ , то есть $OD = 3$ . Из теоремы Пифагора для треугольника $SOD$ получаем $SD =√10-$ , откуда $7√10 DL = 10$ . По теореме косинусов для $△ADC$ имеем $√-- 2 21$ , а значит $√ -- TC = 21$ . По теореме Пифагора для $△SOC$ вычислим $√-- SC = 22$ . Заметим, что для треугольника $SDC$ выполняется теорема Пифагора, то есть угол $SDC$ прямой. С помощью теоремы косинусов для треугольника $SAD$ вычислим $3√30 cosSDA = 20$ . Теперь через теоремы косинусов для треугольников $LDI$ и $LDH$ вычислим длины отрезков $7√10- 7√85- IL = 5 ,LH = 10$ . Далее по теореме Герона получаем $147- S△ILH = 20$ .

Заметим, что $1 1 5 3 15 S△MHG = 2sin∠MHG ⋅MH ⋅GH = 2sin∠MHG ⋅7HL⋅ 7HI = 49S△HLI$ . Значит, $34 34 147 51 SLMGI = S△LHI − S△MHG = 49S△LHI = 49-⋅20 = 10$ .

Ответ: 5.1

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#69311

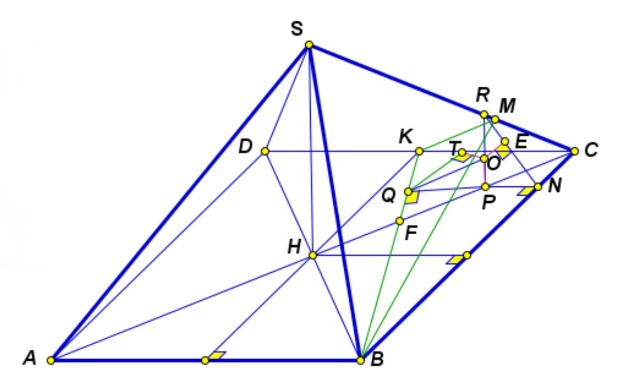
Найдите площадь сечения правильной шестиугольной пирамиды $SABCDEF$ плоскостью, проходящей через вершину $F$ основания $ABCDEF$ и параллельной медиане $CM$ боковой грани $SCD$ и апофеме $SN$ боковой грани $SAF,$ если сторона основания пирамиды равна $√- 4 7,$ а расстояние от вершины $S$ до секущей плоскости равно $√- 7.$

Источники: ШВБ-2023, 11.6 (см. olymp.bmstu.ru)

Подсказки к задаче

Подсказка 1

Итак, перед нами стереометрия с ШВБ, технической олимпиады, а значит придётся много считать и не бояться этого. Но для того, чтобы найти площадь сечения, нужно сначала его построить, что не очень просто, ведь пирамида аж шестиугольная. Однако нам дано целых две прямые, параллельные сечению, поэтому, хорошей идеей для начала решения будет постpоение разных прямых, параллельных данным в некоторых плоскостях.

Подсказка 2

Построим прямую SQ, параллельную CM, точка Q принадлежит CD. Что теперь можно сказать про отношение плоскостей SQN и сечения?

Подсказка 3

Они параллельны! Через точку F проведём прямую, параллельную NQ, пусть она пересекает CD в точкe V. Правда ли, что эта прямая принадлежит сечению?

Подсказка 4

Да, это верно! Через точку V проведем прямую VL, параллельную CM, L лежит на SC. Получается, плоскость FVL — плоскость сечения. Теперь нетрудно найти точки, в которых эта плоскость пересекает плоскость пирамиды.

Подсказка 5

Ура, мы построили сечение! Но получился пятиугольник, как теперь искать его площадь? Вспомните формулу: Площадь сечения равна площади проекции сечения на основание делить на угол между плоскостями сечения и основания.

Подсказка 6

Дальше дело техники! Площадь проекции найдите как сумму площадей треугольников. Длины различных отрезков можно искать и выражать через длину стороны основания с помощью подобия, теоремы Фалеcа. Не забывайте так же про большое количество параллельных прямых на чертеже и правильность шестиугольника в основании. А для того, чтобы найти угол, нужно вспомнить про данное в условии расстояние!

Показать ответ и решение

Построим сечение пирамиды. В плоскости $SCD$ через точку $S$ проведем прямую $SQ,$ параллельную $CM,$ $Q$ принадлежит прямой $CD.$ Тогда $CM$ будет средней линией треугольника $SQD,$ следовательно, $QC = CD = a,$ где $a$ — сторона основания пирамиды.

Плоскость $SNQ$ содержит прямые $SN$ и $SQ,$ которые параллельны плоскости сечения, следовательно, по признаку плоскость $SNQ$ параллельна плоскости сечения.

$PIC$

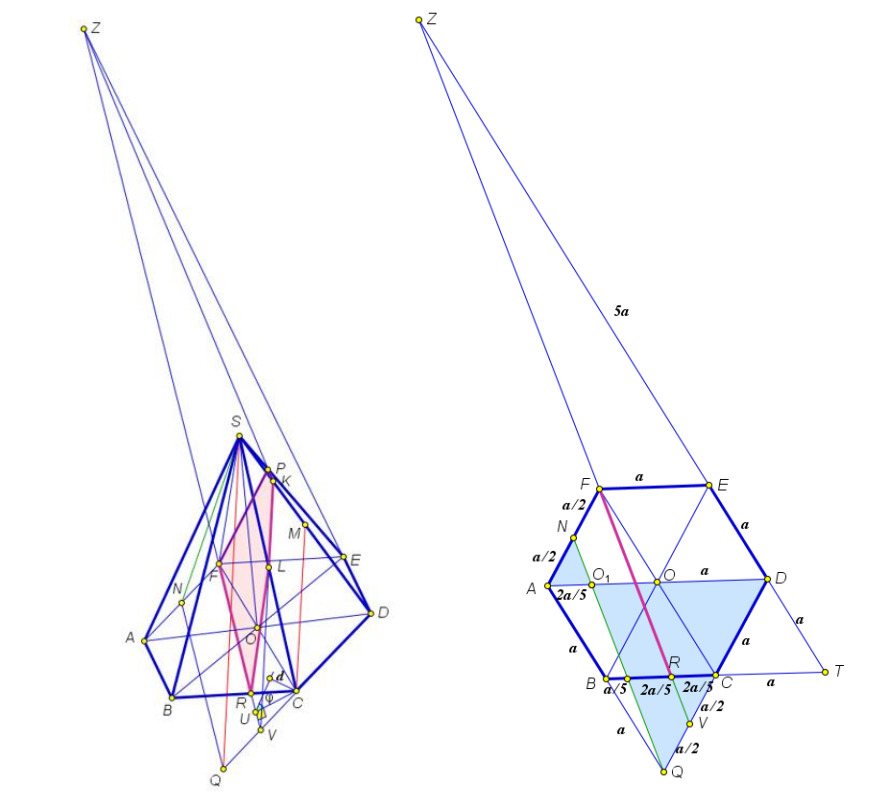
Через точку $F$ проведем прямую $FV,$ параллельную $NQ,$ где $V$ принадлежит прямой $CQ.$ Т.к. $AF ∥CD$ и $NQ ∥F V,$ значит, $NF VQ$ — параллелограмм, следовательно, $NF = QV.$ Учитывая, что $N$ — середина $AF,$ а также $V C = QC − QV =a − QV,$ можем сказать, что $QV = VC =a∕2.$

Пусть $R$ — точка пересечения прямых $FV$ и $BC.$ Плоскость сечения пересекает основание пирамиды по отрезку $FR.$

Пусть $O 1$ — точка пересечения $NQ$ и $AD.$ Заметим, что углы $AO N 1$ И $DO Q 1$ равны как вертикальные, а углы $NAO 1$ и $O DQ 1$ как накрестлежащие при параллельных прямых $AF$ и $CD$ и секущей $AD.$ Следовательно, треугольники $AO N 1$ и $DO Q 1$ подобны, поэтому

AO1- AN- a∕2 1 O1D = QD = 2a = 4

Т.к. $ABCDEF$ является правильным шестиугольником, значит, $AD = 2a.$ Учитывая, что $AO1 :O1D =1 :4,$ получаем, что $AO1 = 2a∕5.$ Т.к. $AD ∥BC$ и $AF ∥ CD,$ углы $RCV$ и $O1AN$ равны, аналогично, т.к. $AF ∥CD$ и $FV ∥NQ,$ углы $RV C$ и $O1NA$ равны, а также $AN = VC =a∕2,$ следовательно, треугольники $RCV$ и $O1AN$ равны, поэтому $RC = AO1 =2a∕5.$

Пусть точка $Z$ — точка пересечения прямых $RF$ и $DE,$ а точка $T$ — точка пересечения прямых $BC$ и $DE.$ Из-за того, что $ABCDEF$ — правильный шестиугольник, можно сделать вывод, что $CT =DT = a.$ Т.к. $F E ∥ BC,$ треугольники $FZE$ и $RZT$ подобны, поэтому

ZE-= --ZE---= FE-= --a----= 5⇒ ZE = 5a ZT ZE +2a RT 2a∕5+ a 7

В плоскости $SCD$ через точку $V$ проведем прямую $V K,$ параллельную $CM,$ $K$ принадлежит ребру $SD,$ $L$ — точка пересечения прямой $V K$ с ребром $SC.$ $CM, VK,SQ$ параллельны друг другу, поэтому по теореме Фалеса имеем

SK-- SK- 1 SK :KM :MD = QV :V C :CD = 1:1 :2 ⇒ KM = 1 и KD = 3

SL SK LC-= KM--=1

В плоскости $SDE$ точка $P$ — точка пересечения прямых $ZK$ и $SE.$ Запишем теорему Менелая для треугольника $SDE$ и секущей $KZ$

DKKS ⋅ SPPE-⋅ EZZD-= 1

3⋅ SP-⋅ 5= 1 PE 6

SP-= 2 PE 5

Искомое сечение - это $KLRF P.$ Для нахождения площади сечения используем формулу

Sсеч =-Sпр-, cosφ

где $Sпр$ — площадь проекции сечения на плоскость основания, $φ$ — угол между плоскостью сечения и плоскостью основания. Найдем площадь проекции сечения на плоскость основания.

$PIC$

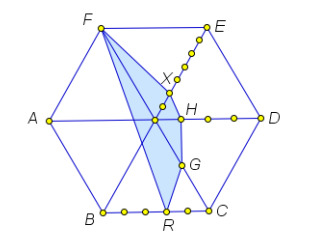
Проекцией является пятиугольник $TXHJR.$ Площадь проекции сечения вычисляется по формуле

Sпр = SFRG +SOGH + SOHX +SOXF

a2√3 2 1 a2√3 1 1 a2√3 1 2 a2√3 2 a2√3 Sпр = 5 − 5 ⋅2 ⋅ 4 + 2 ⋅4 ⋅ 4 +4 ⋅7 ⋅ 4 + 7 ⋅ 4

2√ - √ - Sпр = 30335a⋅323= 30130-3

Обозначим расстояние от точки $S$ до плоскости сечения $d,$ $√- d= 7.$ Т.к. точка $L,$ принадлежащая плоскости сечения является серединой $SC,$ расстояние от точки $C$ до сечения тоже равно $d.$ В треугольнике $RCV$ проведем высоту $CU,$ обозначим ее длину $h.$ Тогда

∘-------- sinφ= d ⇒ cosφ = 1− (d)2 h h

Т.к. $ABCDEF$ — правильный, $∘ ∠RCV = 60 .$ Тогда найдем $RV$ по теореме косинусов:

2 2 2 2 √ -- RV 2 = 4a-+ a-− a = 21a-⇒ RV =--21a 25 4 5 100 10

Используя различные формулы для нахождения площади треугольника $RCV,$ имеем

√-- √- -21ah= a2 ⋅-3⇒ h= a√-- 10 5 2 7

Тогда

∘ ----2- cosφ= 1− 7d2-= 3 a 4

Окончательно имеем

303√3 √- S = --10--= 202-3- сеч 3 5 4

Ответ:

$202√3 5$

Ошибка.
Попробуйте повторить позже

Задача 3#74505

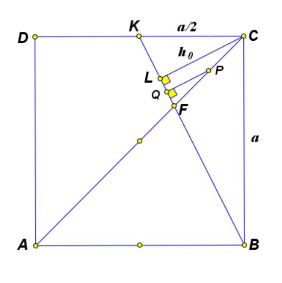
Шар радиуса $4 9$ лежит внутри правильной четырехугольной пирамиды $SABCD$ со стороной основания 8 и высотой 3. Этот шар касается плоскости основания $ABCD$ пирамиды и боковых граней $SBC$ и $SCD.$ Плоскость $γ$ касается шара, проходит через точку $B,$ середину $K$ ребра $CD$ и пересекает ребро $SC$ в точке $M.$ Найдите объем пирамиды $MBCK.$

Подсказки к задаче

Подсказка 1.

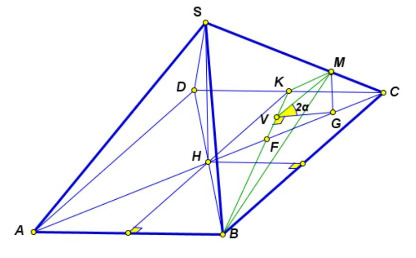
Сразу же введём основание высоты пирамиды (например, через точку H) и центр шара (например, через точку O). Раз в условии у нас правильная пирамида, то центр данного шара лежит в плоскости SHC. Тогда удобно будет провести прямую, проходящую через центр O параллельно SH (пусть это прямая PR). Мы сразу знаем OP, ведь он равен радиусу, а также то, что RP перпендикулярен плоскости основания пирамиды. Введём коэффициент подобия треугольников SCH и RCP (пусть он равен 1/k). Тогда, зная SH, мы можем выразить PR через k. Хорошо бы было выразить ещё отрезки через k, чтобы впоследствии прийти к уравнению и найти k. Попробуйте сделать это в плоскости ABCD.

Подсказка 2.

В плоскости ABCD мы можем провести прямую, проходящую через P параллельно AB. Пусть она пересекает BC в точке N. Тогда, так как ABCD — квадрат, то AH = HC, и с помощью этого мы легко можем выразить PN через AB и k. Теперь можно заметить, что точка касания шара и плоскости SBC лежит на RN. Что тогда мы можем сказать про треугольники ROE и RPN?

Подсказка 3.

Верно, они подобны. Тогда, записав подобие, мы можем получить уравнение на k, откуда k = 1/3. Отлично, теперь пора возвращаться к плоскости из условия. Чтобы найти объём MBCK, нужно найти высоту из M на BCK (пусть это отрезок MG) и площадь треугольника BCK. С треугольником BCK нет никаких проблем, ведь мы знаем сторону квадрата ABCD и отношение CK к KD, а значит, можем найти любой элемент треугольника. Но как же найти MG? Попробуйте выразить его через SH и коэффициент подобия треугольников MCG и SCH (пусть он равен n). Чтобы найти n, можно использовать угол между плоскостями MKB и KBC, опустив высоту GV на BK.

Подсказка 4.

Используя подобие треугольников VFG и FKC (F является точкой пересечения BK и AC), мы можем выразить GV через n. Тогда мы можем выразить тангенс угла MVG через n. Отлично! Теперь осталось лишь найти этот угол. Мы знаем, что он является линейным углом двугранного угла между плоскостями MKB и KBC. Для решения задачи мы ещё не использовали, что плоскость MKB касается шара (пусть точка касания — точка T). Зная это, мы можем опустить перпендикуляр PQ на BK и получить, что TQP также является линейным углом двугранного угла между плоскостями MKB и KBC. Теперь нужно найти угол TQP. Его не очень удобно искать, однако посмотрите на треугольники OTQ и OQP. Попробуйте найти угол, используя их равенство.

Подсказка 5.

Треугольники OTQ и OQP равны, а значит и углы TQO и OQP. Тогда угол TQP в два раза больше угла OQP. А вот угол OQP легко найти, ведь мы можем выразить PQ через подобие треугольников QFP и KFC, а OP мы знаем. Так мы найдём тангенс угла OQP. Затем по формуле тангенса двойного угла найдём тангенс угла TQP и, подставив в уравнение, найдём n. Осталось лишь подставить n в формулу MG и найти объём.

Показать ответ и решение

Поскольку пирамида $SABCD$ правильная, то центр $O$ указанного шара лежит в плоскости $SHC$ , где $SH$ — высота пирамиды. Пусть $RP ∥SH,R∈ SC,P ∈HC,$ $O∈ RP.$

Обозначим $SH = h,AB =a,RP =kh.$ Проведем $PN ∥AB,N ∈BC.$ $E$ — точка касания шара плоскости $SBC,$ пусть радиус шара $OE = r.$ Поскольку $P C :HC = k,$ то $PN = ka∕2.$ Треугольники $ROE$ и $RPN$ подобны, и $OE :PN = RO :RN,$ или

(√ -2---2- ) -r--= -∘-k2h−-r--2, r= √-kh2− r-2, k= r --4h--+a-+ 1 ka∕2 k h +(a∕2) a 4h + a h a

По условию задачи $a =8,h= 3,r= 4. 9$ Тогда $k= 1. 3$

Точка $F$ — точка пересечения $AC$ и $BK,$ тогда $FC = AC∕3.$ Поскольку $P C = kHC =$ $=HC ∕3=$ $AC∕6,FP =P C.$

$PIC$

Пусть $PQ⊥ BK$ . Тогда $-a√- PQ = 2 5.$ Если $α= ∠OQP,$ то $r2√5 √5 tgα= a = 9 .$ Угол между плоскостью $γ$ и плоскостью основания равен $2α.$ Тогда

2tgα 4√5ar 9√5 tg2α = 1− tg2α-= a2-− 20r2 =-38

Пусть $MG$ — отрезок перпендикуляра, опущенного из точки $M$ на плоскость основания $ABC$ , и $MG = nh$ . Тогда $CG =nCH$ . Если $GV ⊥ BK$ , то

GF- AC-∕3-− nAC-∕2 2− 3n GV = CF h0 = AC∕3 h0 = 2 h0,

$a h0 = √5$ — высота треугольника $BCK,$ проведенная из вершины $C.$

√- 2 tg2α= -2nh-5-,n= -----4ra2-----2 = 12 (2− 3n)a (h+ 6r)a − 20hr 37

V = 1⋅ a2nh = 192- MBCK 3 4 37

$PIC$

Ответ:

$192 37$

Ошибка.
Попробуйте повторить позже

Задача 4#74506

В 2022 году исполняется 65 лет запуска первого искусственного спутника Земли (ИСЗ). В настоящее время для обеспечения бесперебойной работы сотовой связи, систем теле и радиовещания используются различные виды спутников, находящихся на различных орбитах, на различных высотах.

Зоной покрытия спутника назовем часть поверхности земного шара, в пределах которой обеспечивается уровень сигналов к спутнику и от него, необходимый для их приема с заданным качеством в конкретный момент времени. Как правило, эта часть поверхности ограничивается окружностью, проходящей по линии видимого горизонта. На рисунке линия проходит через точку Г:

$PIC$

a) Определите площадь земной поверхности ( $в км2$ ), которая является зоной покрытия спутника, находящегося на высоте $H = 500$ км относительно земной поверхности, считая ее сферой радиуса $R = 6400$ км с центром в точке $O.$

б) Найдите все значения $n >1,$ для которых на поверхности земли можно расположить окружности $C1,...,Cn,$ каждая из которых внешним образом касается окружности $C0,$ с центром в точке $A$ и радиусом $r< R,$ каждая из них является границей зоны покрытия ИСЗ, находящегося на той же высоте $H$ , что и спутник с зоной покрытия $C0.$ Каждая из зон покрытия $Ci$ должна внешним образом касаться окружностей $C0$ и $Ci+1,i=0,1,...,n− 1,$ т.е. первая касается $C0$ и $C2,$ вторая — $C0$ и $C3,$ и т.д. Окружность $Cn$ должна касаться $C0$ и $C1.$

Источники: ШВБ-2022, 11 (см. olymp.bmstu.ru)

Подсказки к задаче

Пункт а, подсказка 1

Вспомним формулу площади шарового сегмента: S = 2πR*h, где h = АЗ. Осталось только найти h и посчитать

Пункт б, подсказка 1

Пусть В — точка касания C₀ и C₁, а З, З₁, З₂ — точки пересечения радиусов сферы, проходящих через центры окружностей. sin(а) можно найти из треугольника АВО. Заметим равенство углов ЗОВ и ВОЗ₁, что делает угол ЗОЗ₁ равным 2а. Найдем ЗЗ₁ через равенство треугольников ОГВ и ОЗ₁З(по двум сторонам и углу). Как нам связать это с количеством окружностей?

Пункт б, подсказка 2

Через двугранный угол при ребре ОЗ. Он будет зависеть от количества таких окружностей и равняться 360°/n

Пункт б, подсказка 3

Чтобы его выразить, опустим перпендикуляры из точек З₁ и З₂ на ребро ОЗ. Пирамида ОЗЗ₁З₂ правильная, поэтому З₁Н и З₂Н пересекутся в одной точке Н и будут равны. Теперь нам нужно их найти.

Пункт б, подсказка 4

Рассмотрим треугольник З₂НЗ₁. Выразим З₂З₁, которую мы уже знаем, через З₁Н и половину угла З₂НЗ₁. Из уравнения выразим sin(180°/n). Осталось только его оценить и получить из этого оценку на n!

Показать ответ и решение

$PIC$

а) Зона покрытия — часть сферы, лежащая внутри конуса. $S = 2πR⋅h$ , где $h= A3$ — высота сегмента. $h =R − R cosα$ , здесь угол $α$ — угол между радиусом ОГ и линией ОА, соединяющий центр сферы с центром окружности, которая является линией пересечения сферы и конуса.

Тогда площадь равна

( ) S = 2πR2(1− cosα)= 2πR2 1−--R-- = 2πR2⋅--H-- ≈ R +H R + H

2 500- 2 10 4096- 5 5 2 ≈6 ⋅6400 ⋅6900 =6400 ⋅23 ≈ 23 ⋅10 ≈178,09⋅10 = 17809000 км

б) Пусть О — центр сферы, В — точка касания первой и второй окружности, А и $A1$ их центры этих окружностей, $З,З1,З2$ — точки пересечения радиусов $R$ со сферой. Обозначим $α$ — угол между ОЗ и ОВ. Тогда $r- sinα = R,ЗЗ1 = 2r.$

$PIC$

В правильной пирамиде О $ЗЗ1З2$ плоские углы при вершине равны $2α,$ двугранный угол при ребре О3 равен $360∕n.$ Опустив перпендикуляры из точек $З1$ и $З2$ на ребро О3 в точку H, треугольники О $З,З1$ и О $ЗЗ2$ равны (по трем сторонам), т.к. две стороны равны $R,$ а третья $2r.$

$PIC$

∘ -------- НЗ1 =Н З2 = 2rcosα= 2r∘1−-sin2α =2r 1− ( r)2 R

∘----r2- ⇒ 2r=ЗЗ1 =ЗЗ2 =2⋅Н З1⋅sin(180∕n)= 4r 1− R2-sin(180∕n)

∘ ------ ( ∘ -----) r2 r2 2 1− R2 sin(180∕n)= 1⇒ sin(180∕n)= 1∕(2 1− R2) > 1∕2⇒ n< 6

Ответ:

а) $17809000$

б) $2,3,4,5$

Ошибка.
Попробуйте повторить позже

Задача 5#97397

Найдите площадь сечения правильной треугольной призмы $ABCA B C 1 1 1$ плоскостью, которая параллельна диагонали $AC1$ боковой грани $AA1C1C,$ проходит через середину стороны $AB$ основания $ABC$ и точку $M,$ лежащую на стороне $B1C1,$ если, $MC1 =3B1M,$ расстояние между $AC1$ и секущей плоскостью равно $3,$ а сторона основания призмы равна $√-- 2 14.$

Показать ответ и решение

В плоскости основания $ABC$ проводим прямую $EA$ параллельную $B C 1 1$ , $EA = MC 1$ , и прямую $ME$ параллельную $AC ,ME 1$ лежит в плоскости сечения. В плоскости основания $ABC$ проводим прямую, соединяюшую точку $E$ с серединой $D$ стороны $AB$ , точка $K$ — точка пересечения этой прямой со стороной $BC$ . В плоскости основания $A1B1C1$ проводим прямую $MN$ , параллельную $DK$ Точка $N$ — точка пересечения прямой $MN$ со стороной $A1B1$ . Трапеция $DKMN$ — искомое сечение.

Найдём площадь проекции сечения на плоскость основания призмы. Обозначим сторону основания через $a$ . Тогда $3a- a BK = 4 ,BD = 2$ . Пусть $Q$ — проекция точки $M$ на основание $a ABC,BQ = 4$ . Пусть $G$ — проекция точки $N$ на основание $ABC$ . Поскольку $GQ$ и $DK$ параллельны, то $BQ :BK =BG :BD$ , и $a BG = 6$ . Проекцией сечения на плоскость основания $ABC$ является трапеция $DKQG$ , её площадь

( ) 2√- √ - Snp = SBDK − SBGQ = SABC 3⋅ 1 − 1 ⋅ 1 = 1SABC = a-3 = 14-3. 4 2 4 6 3 12 3

Найдём косинус угла $α$ наклона плоскости сечения к плоскости основания призмы. Расстояние $d$ от прямой $AC1$ до плоскости сечения равно расстоянию от точки $A$ до плоскости сечения, которое, в свою очередь, равно расстоянию от точки $B$ до плоскости сечения ( $AD = DB$ , где $D$ принадлежит плоскости сечения).

Строим плоскость $BHL$ , проходящую через точку $B$ и перпендикулярную $DK$ линии пересечения основания и плоскости сечения ( $BH$ и $LH$ перпендикулярны $DK$ ). Проведем прямую $BP$ перпендикулярную $LH$ , расстояние $d$ равно $BP$ . Угол наклона плоскости сечения к плоскости основания равен углу $BHL$ . Находим: