Алгебраические текстовые задачи на ШВБ
Ошибка.
Попробуйте повторить позже
Сотовая связь — это целый мир возможностей. Но чтобы пользоваться ими, нужно быть в зоне действия базовой станции. Сети GSM (2G) имеют мощность, которая позволяет покрывать территорию радиусом до 35 километров на открытой местности. В городских условиях, где много зданий, зона приема сигнала значительно уменьшается. Сети 3G и 4G (LTE) работают на более высоких частотах, чем сети 2G, и их сигнал хуже проникает сквозь препятствия и больше подвержен помехам. В сетях GSM было достаточно нескольких вышек, чтобы покрывать большие территории, а для 3G и 4G сетей для обеспечения надежной связи требуется больше вышек.
В городе установлен ретранслятор GSM сети, который обеспечивает покрытие в пределах окружности радиусом км. Центр
окружности — основание вышки. Однако из-за особенностей рельефа зона покрытия этого ретранслятора ограничена хордой, проведенной
внутри этой окружности. Хорда находится на расстоянии
км от центра окружности.
В меньшем сегменте, образованном хордой, необходимо установить два дополнительных ретранслятора (3G вышки) так, чтобы их зоны
покрытия касались друг друга, хорды и основной окружности. Каждый из этих ретрансляторов имеет круговую зону покрытия одинакового
радиуса
Найдите радиусы зон покрытия двух дополнительных ретрансляторов, которые нужно установить в меньшем сегменте. Определите площадь части меньшего сегмента, которая не попадает в зону действия дополнительных ретрансляторов.
Источники:
Подсказка 1
Изобразим условие на рисунке. Пусть O — центр окружности, в радиусе которой действует GSM вышка, AB —хорда, OP = d — расстояние от основания вышки до хорды, C и D — основания 3G вышек. Что можно сказать про их расположение, исходя из условия?
Подсказка 2
Верно! Они касаются прямой OP в одной точке (пусть K)! Проведём радиусы в точки касания. Какая теорема поможет найти нам радиус малых окружностей?
Подсказка 3
Конечно! Давайте применим теорему Пифагора для △OCK, предварительно выразив отрезки OC и OK через радиус малой окружности и данные в условии величины. А что делать с площадью части меньшего сегмента, которая не попадает в зону действия вышек?
Подсказка 4
Введите угол с вершиной O и выразите искомую площадь, равную разности площадей сегмента и площади, которую покрывают 3G вышки.
Подсказка 5
△OPA — прямоугольный. Пусть ∠POA = α. Тогда cos(α)=OP/OA = d/R — известное нам отношение! Значит через этот угол можно выразить нужные нам площади! Осталось только аккуратно посчитать и записать ответ!
Пусть вышки имеют одинаковый радиус действия
Радиус основной окружности
расстояние от центра большой окружности до
хорды
Введем точки, как показано на чертеже:
— центр большой окружности,
— центры маленьких окружностей,
—
точка касания маленьких окружностей,
— точка касания окружности с хордой.
— заданное расстояние от центра до хорды
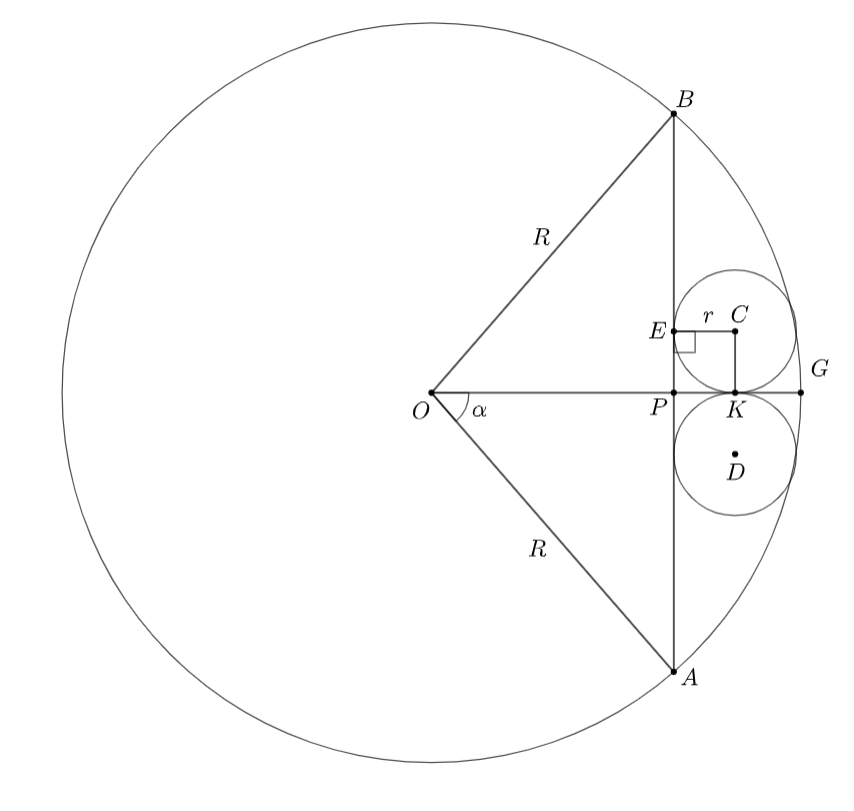
Тогда из рисунка понимаем следующие вещи:
Запишем теорему Пифагора для и выразим меньший радиус:
Подсчитаем площадь части сегмента, которая не попадает в зону действия ретрансляторов
Пусть
Выразим нужные нам синусы и косинусы углов, а потом посчитаем нужную площадь как разность:
Подставим значения
Итого, подставив все значения, получаем конечный ответ:
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




