Алгебраические текстовые задачи на ШВБ

Во всем мире популярна игра в хоккей. Многое в игре зависит от вратаря. Для отработки навыков вратарей и обеспечения тренировочного процесса, который бы не зависел от других игроков, создали шайбомет. Автомат можно настроить так, чтобы он выбрасывал шайбы с заданной временной частотой, скоростью и под определенным углом.

Пусть линия ворот находится на расстоянии 25 м от центральной точки хоккейной площадки. Автомат установлен на расстоянии м от точки по направлению к воротам, скорость выброса шайбы равна м/c. Броски производятся в плоскости, перпендикулярной поверхности льда и линии ворот. При этом для обеспечения безопасности траектория вылетающих шайб должна, с одной стороны, находиться не выше прямой линии, соединяющей центр ледовой площадки с точкой, находящейся в плоскости полета шайб, в плоскости ворот, и на расстоянии одного метра от поверхности льда, а с другой стороны — должна пересекать плоскость ворот по нисходящей ветви траектории.

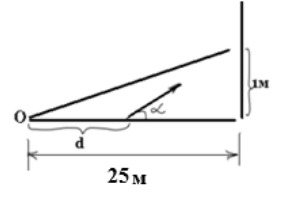
Определите максимально возможное значение тангенса угла, под которым могут вылетать шайбы из шайбомета, если траектория движения шайбы, рассматриваемой как материальная точка, в плоскости ее полета в системе координат с центром в и осью абсцисс, направленной вдоль поверхности льда, описывается уравнениями

Для упрощения вычислений можно считать, что ускорение свободного падения м/c