Стереометрия на ШВБ
Ошибка.
Попробуйте повторить позже
Искусственный спутник (ИСЗ) движется по круговой орбите вокруг Земли (имеет форму шара) на высоте 
равной радиусу Земли
км, с периодом обращения 
ч и постоянной угловой скоростью 
Для того, чтобы можно было наблюдать за
спутником с поверхности Земли, он должен находиться выше плоскости горизонта. Определите:
а) продолжительность наблюдения спутником (в минутах) от момента его появления над горизонтом до момента захода за горизонт, если траектория ИСЗ проходит ровно над головой наблюдателя;
б) плоский угол при вершине конуса обзора поверхности Земли с ИСЗ (в градусах).
Источники:
Пусть наблюдатель находится в точке 
— линия пересечения плоскости горизонта и плоскости орбиты. Спутник проходит над
головой наблюдателя.
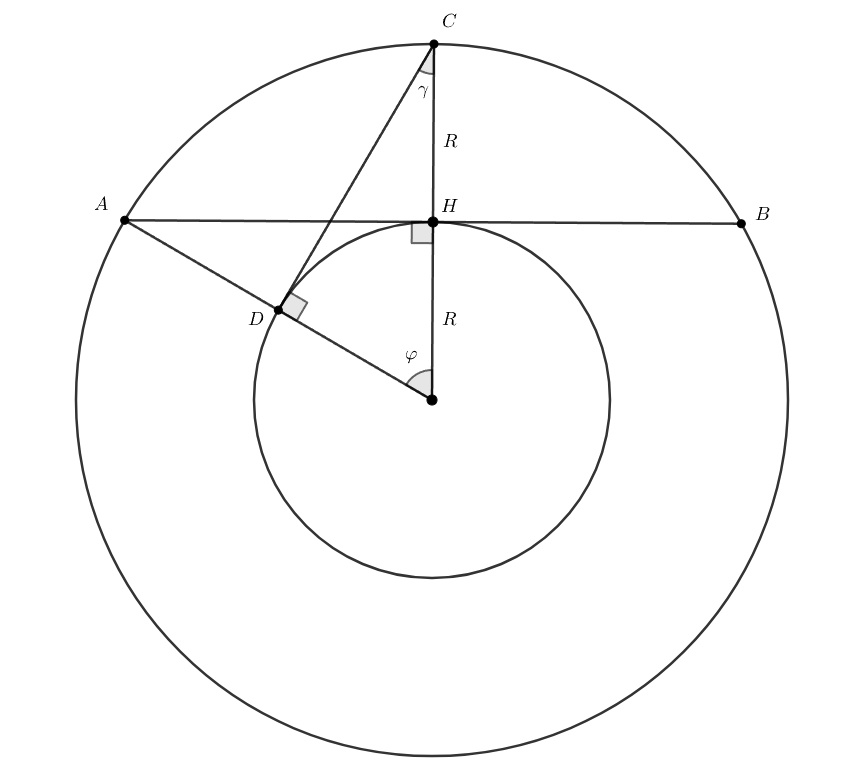
При движении спутника из точки 
в точку С по дуге окружности, его проекция на Землю двигается из точки 
в
точку 
Угловая мера этой дуги 
равна величине центрального угла. Учитывая симметрию, получим время
наблюдения
Угол находим из прямоугольного треугольника
следовательно, 
мин.
Угол обзора участка Земли с орбиты равен углу 
или 
градусов.
а) 
минут, б) 
градусов
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
