Стереометрия на ШВБ
Ошибка.
Попробуйте повторить позже
На боковых рёбрах правильной треугольной пирамиды
соответственно выбраны точки
так, что
. Точка
— центр сферы, описанной около пирамиды
Докажите, что прямая
перпендикулярна
плоскости
Найдите радиус этой сферы и объём пирамиды
если сторона основания
боковое ребро
Подсказка 1
Посмотрим на цепочку соотношений из условия, которая равна 3. Почему именно эти отношения влияют на расположение точек A₁, B₁, C₁ на рёбрах пирамиды? Возможно, стоит посмотреть на подобия каких-то треугольников.
Подсказка 2
Иногда можно использовать идею проецирования центра сферы на разные плоскости. Подумайте, почему такая проекция на боковые грани позволяет утверждать, что есть общий перпендикуляр к двум прямым, пересекающимся на плоскости из условия.
Подсказка 3
Воспользуемся теоремой о трёх перпендикулярах. К какой прямой и плоскости её стоит применить?
Подсказка 4
Применяем теорему о трёх перпендикулярах к TO и пересекающимся B₁C и A₁C в плоскости A₁B₁C и доказываем требуемое. Теперь перейдём ко второй части задачи. Для этого полезно рассмотреть высоту пирамиды и вспомнить, что в основании неё лежит равнобедренный треугольник. Подумайте, какие дополнительные точки (например, на рёбрах пирамиды) могут упростить вычисления.
Подсказка 5
Для нахождения объёма пирамиды может оказаться нужным найти её высоту, введя дополнительный угол и его синус/косинус, установить, каким отношением связаны основания A₁B₁ и AB и использовать тот факт, что T лежит на TO, которая по доказанному перпендикулярна плоскости из условия. Для нахождения радиуса вспоминаем формулу со стороной и синусом противолежащего угла!
1) Докажем, что прямая перпендикулярна плоскости
Точка
лежит в плоскости
,
— середина
Спроецируем
точку
на плоскость
ее проекция
центр описанной около треугольника
окружности. Прямая
— проекция
на плоскость
Докажем, что
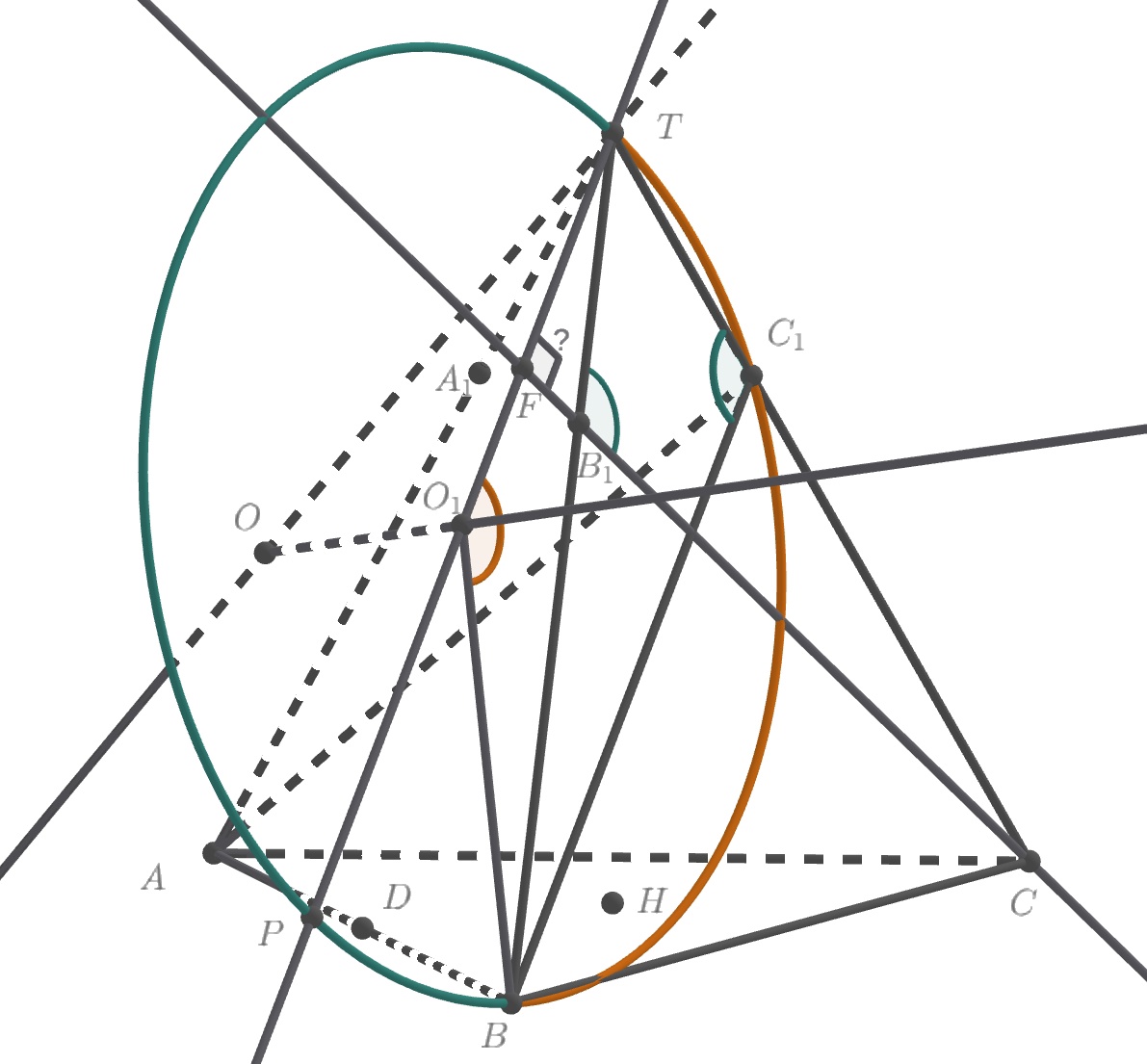
Поскольку то
подобен
тогда
Докажем, что
т.е.
— точка пересечения прямых
и
По свойству вписанных углов
имеем:
Пусть — диаметр рассматриваемой окружности. Тогда
Таким образом,
Аналогично доказывается, что проекция на плоскость
перпендикулярна
Согласно теореме о трех перпендикулярах,
также будет перпендикулярна двум пересекающимся прямым
и
лежащим в плоскости
следовательно,
2) Обозначим через длину стороны основания пирамиды
Обозначим через
длину бокового ребра пирамиды
Пусть
— высота пирамиды
Тогда
В основании пирамиды
лежит
равнобедренный треугольник
— его высота,
— середина
Высота
пирамиды
проведенная из вершины
лежит на прямой
Для вычисления объема пирамиды
нужно найти
и
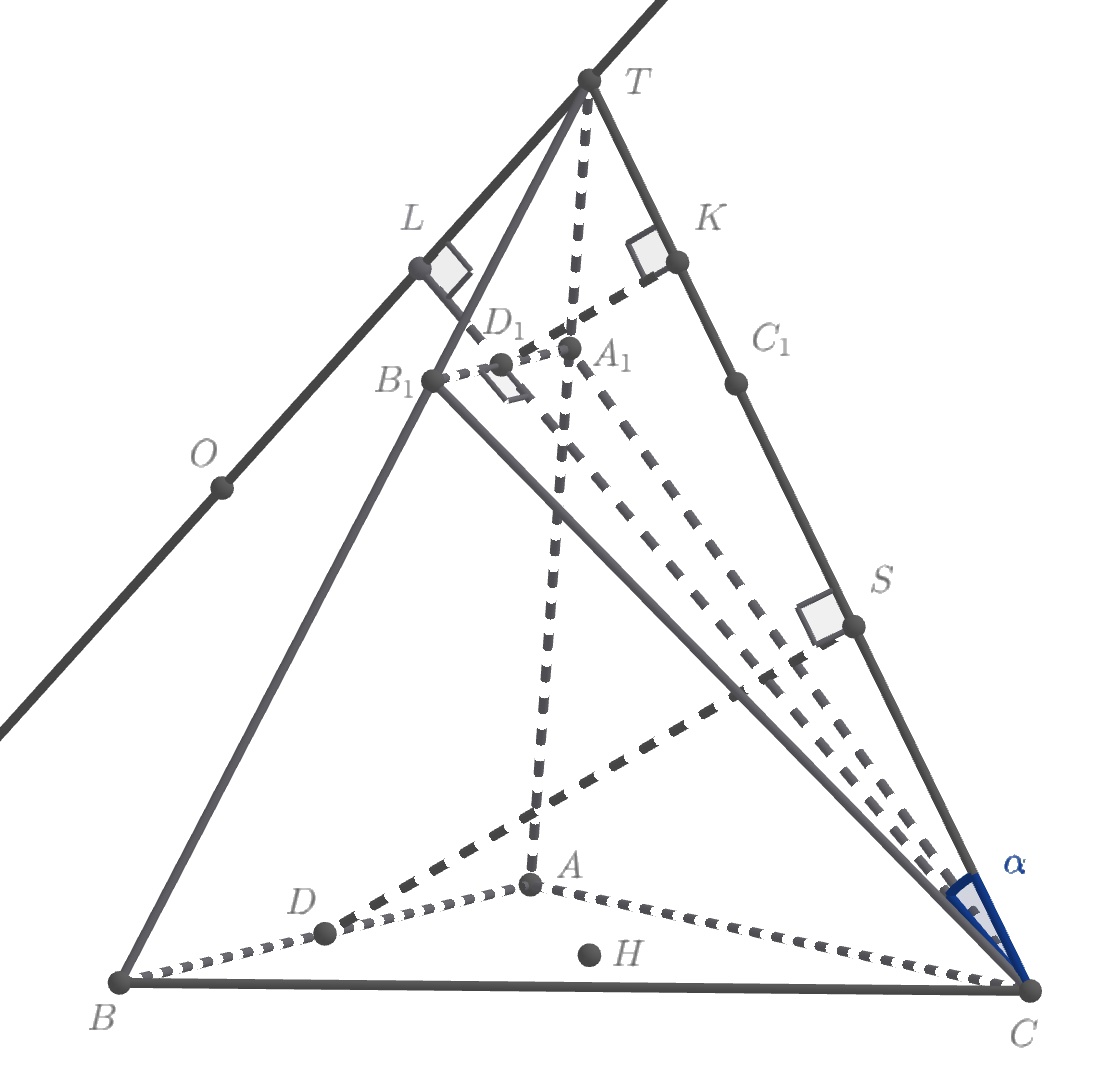
На боковом ребре отметим точки
и
так, что
Пусть Тогда
Значит,
Итак, объем пирамиды вычисляется по формуле
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




