Стереометрия на ШВБ
Ошибка.
Попробуйте повторить позже
В правильной усеченной четырехугольной пирамиде сторона нижнего основания
равна 24, верхнего основания
равна 12, высота пирамиды
равна
, точка
— центр основания
Поверхность
многогранника
состоит из квадрата
, боковых граней пирамиды
и боковых граней пирамиды
. Найдите площадь сечения многогранника
плоскостью, проходящей через точки
и середину ребра
.
Источники:
Подсказка 1
Для построения сечения достаточно внимательности и базовых навыков, которые у вас должны быть после школьной стереометрии. Когда находите точки пересечения плоскости с прямыми, также находите отношения, в которых эти точки их делят. Для этого может понадобиться теорема Менелая.
Подсказка 2
Чтобы искать площадь было удобнее, спроецируйте ортогонально сечение на плоскость основания, найдите плоскость проекции, затем поделите на косинус угла между плоскостями сечения и основания.
Подсказка 3
Площадь проекции можно представить в виде суммы и разности площадей некоторого количества треугольников.
Подсказка 4
Осталось найти косинус угла между плоскостями сечения и основания. Давайте заметим, что они пересекаются по прямой l, проходящей через D параллельно F₁C₁ (F₁ — середина A₁ и B₁). Пусть C₁' — проекция C₁ на основание, а H — основание перпендикуляра из C₁ на l. Нужно аккуратно посчитать косинус угла C₁'HC₁.
Пусть
высота пирамиды
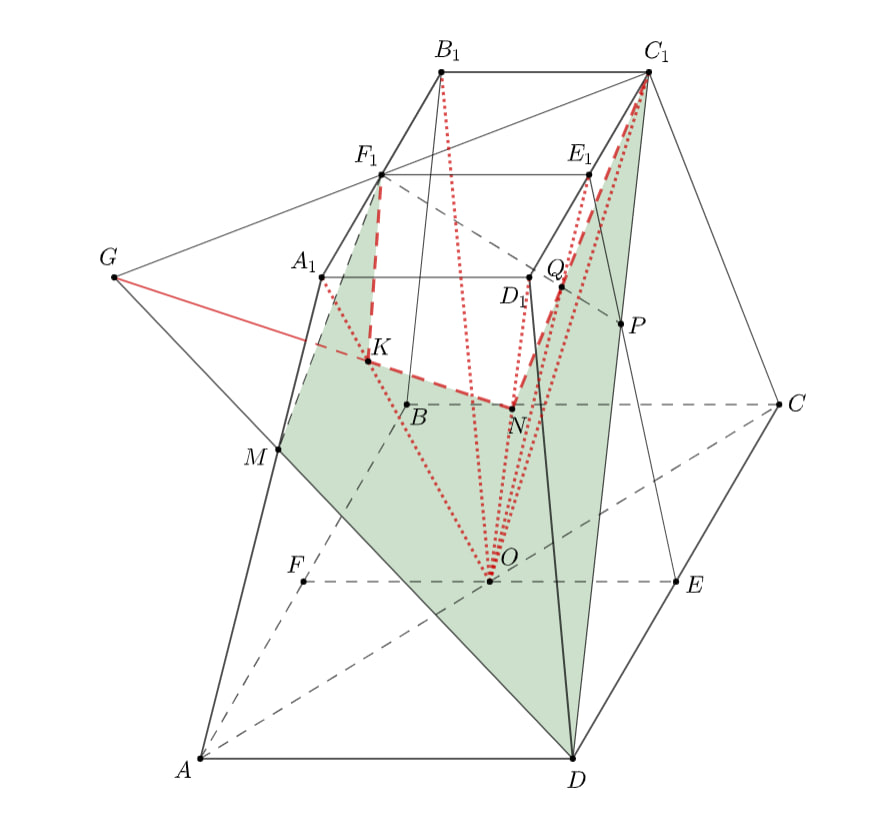
Построение сечения:
- Точки
и
— середины
и
- Точки
и
— середины
и
- Прямая
принадлежит плоскости сечения. Найдем точку
пересечения этой прямой с
- Точки
и
лежат в плоскости грани
Прямая
принадлежит плоскости сечения. Найдем точку
пересечения с ребром
- Треугольники
и
равны,
Из подобия
Точка :
— пересечение прямых
и
значит, лежит в плоскости сечения.
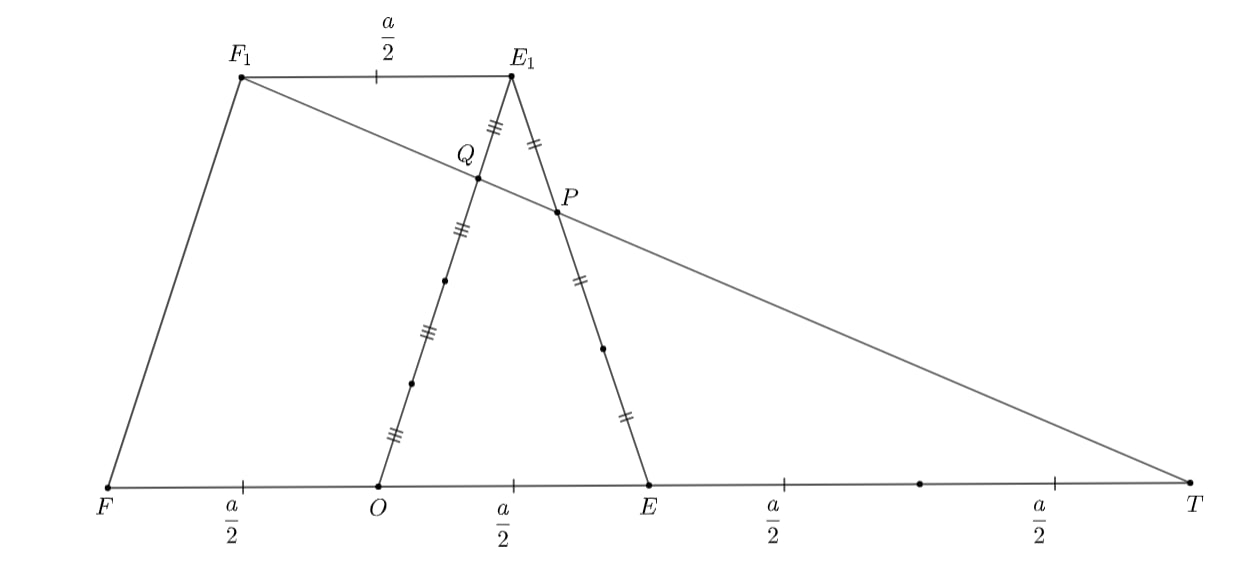
Точки и
:
- В плоскости трапеции
проведем
Точка
— пересечение
с
лежит в плоскости сечения.
- Из подобия треугольников
- Из подобия
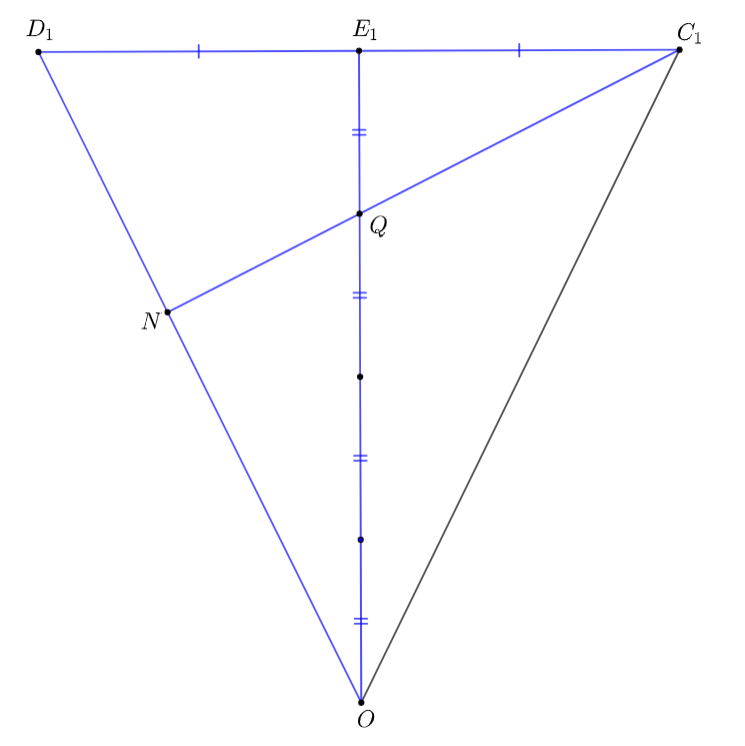
Точка :
-
Прямая
пересекает
в точке
По теореме Менелая:
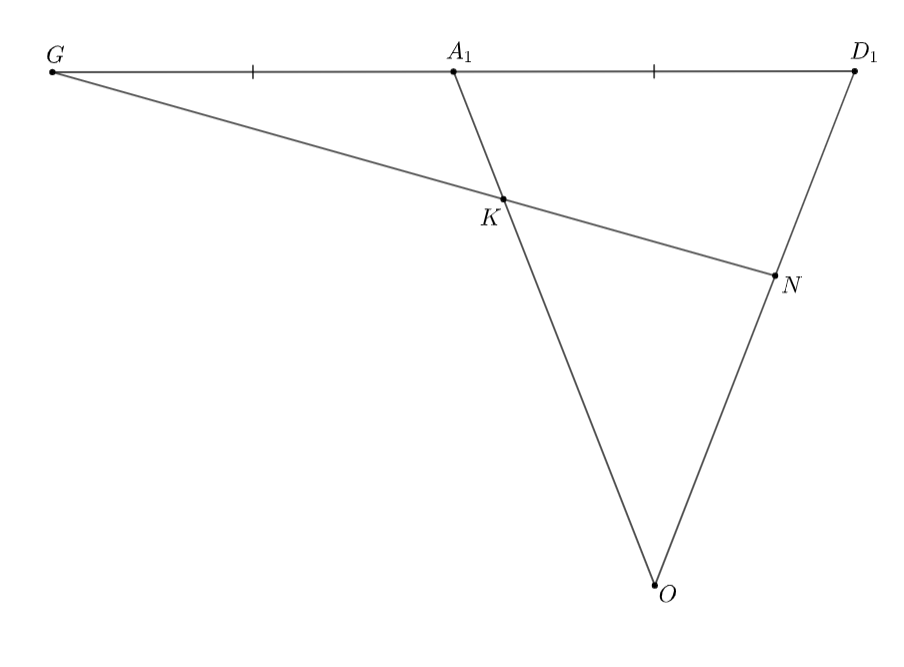
Точка :
-
Прямая
пересекает
в точке
По теореме Менелая:
Получили сечение, это многоугольник
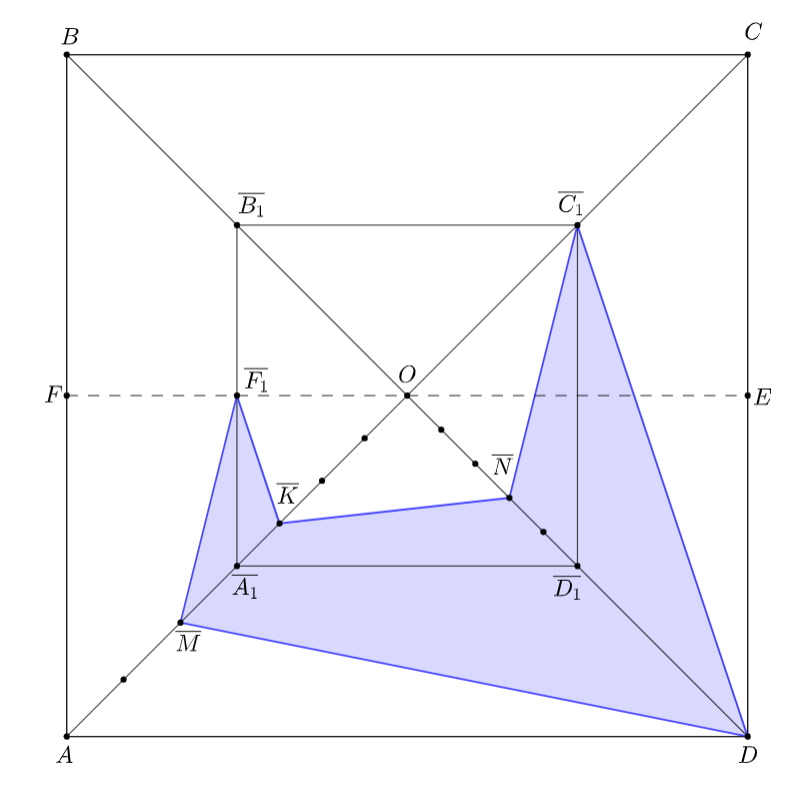
Площадь сечения:
Проекция сечения: Спроецируем все на плоскость основания, учитывая что отношения в которых делят отрезки
точки
известны и сохраняются при проекции, то все отрезки с изображения проекции известны. Тогда подсчитаем площадь
проекции как:
Угол :
Плоскость сечения и плоскость нижнего основания пересекаются по прямой
проходящей через точку
и параллельной
прямой
Если
— проекция точки
на плоскость нижнего основания, то
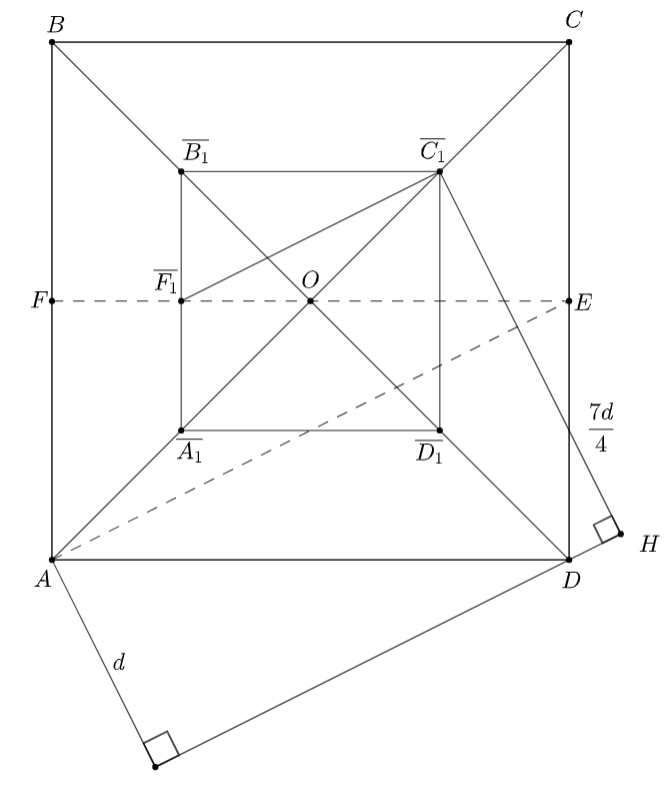
Из точки опустим перпендикуляр
на прямую
Если
— высота треугольника, то
Угол равен
— углу между плоскостью сечения и плоскостью основания.
Итоговая площадь:
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




