Стереометрия на ШВБ
Ошибка.
Попробуйте повторить позже
В правильной усеченной четырехугольной пирамиде сторона нижнего основания
равна
верхнего
основания
равна
точка
— центр основания
Поверхность многогранника
состоит из квадрата
боковых граней пирамиды
и боковых граней пирамиды
Найдите площадь сечения
многогранника
плоскостью, содержащей прямые
и
если расстояние от точки
до плоскости сечения равно
Источники:
Подсказка 1
Сначала надо разобраться с сечением. Достройте усечённую пирамиду до пирамиды.
Подсказка 2
Рассмотрите середины отрезков AB, CD, A₁B₁ и C₁D₁.
Подсказка 3
Пусть F — середина AB, Е₁ — середина C₁D₁. Заметим, что прямая FE₁ принадлежит плоскости сечения. Найдем точку её пересечения с гранью OA₁B₁.
Подсказка 4
В данной конструкции появляется много подобных треугольников, пользуйтесь ими.
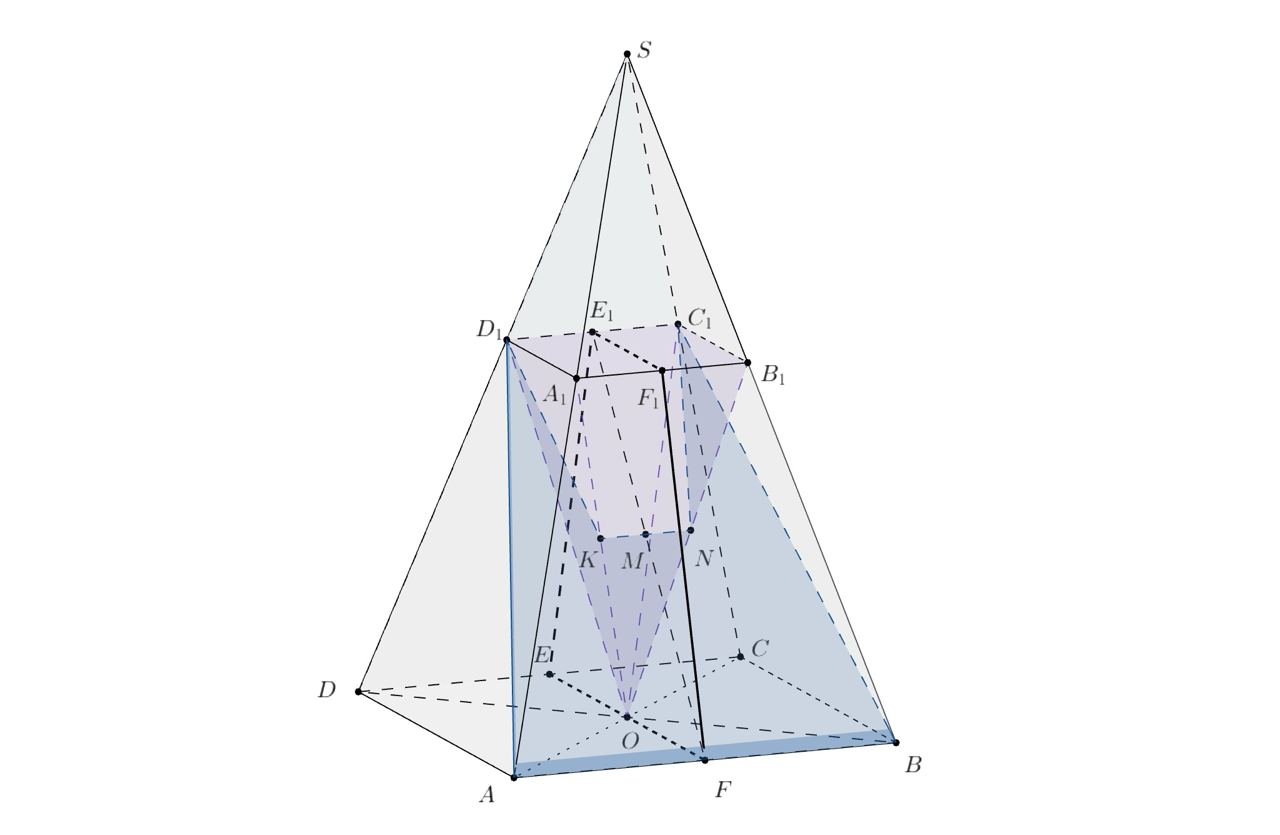
Пусть расстояние от точки
до плоскости сечения обозначим
Построим сечение многогранника
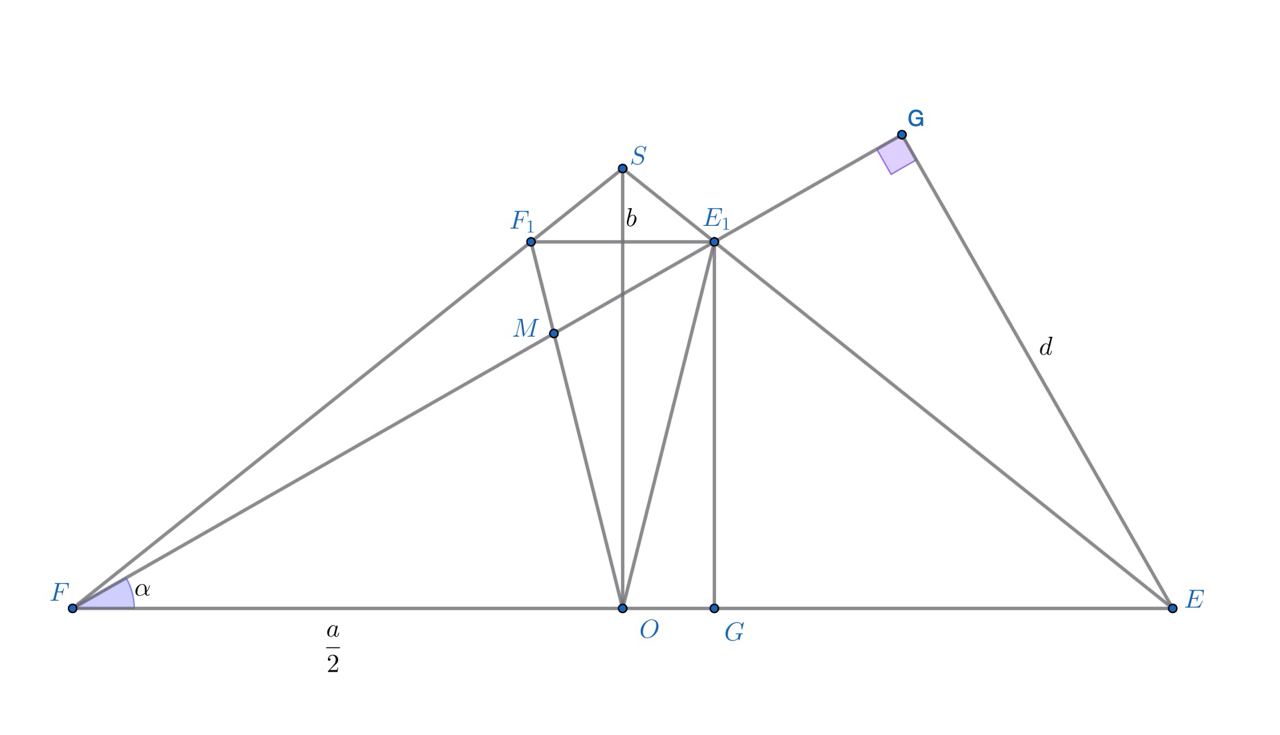
Достроим усеченную пирамиду до пирамиды
продолжив ребра
Пусть точки
и
— середины
и
соответственно,
и
— середины
и
соответственно. Прямая
принадлежит плоскости
сечения. Найдем точку
пересечения этой прямой с гранью
Эта точка лежит на прямой
Треугольники
и
подобны, и
Через точку в плоскости
проведем прямую
так, что
лежит на
лежит на
Сечением
многогранника
будет многоугольник
Его площадь равна разности площадей трапеций
и
Высотой
трапеции
является отрезок
а трапеции
— отрезок
Обозначим Тогда
Пусть
принадлежит
Тогда
Значит,
Следовательно,
Отсюда Треугольники
и
подобны, и
Теперь найдем площади интересующих нас четырехугольников:
В итоге получаем
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




