Стереометрия на ШВБ

Пусть — середина ребра а точка - середина отрезка . Рассмотрим плоскость . Так как плоскость сечения параллельна медиане и проходит через точку , построим прямую в плоскости . Тогда - средняя линия в , а середина .

Теперь нам известны три точки сечения: . Рассмотрим основание пирамиды и посмотрим, как прямая пересекает стороны основания. Пусть эта прямая пересекает прямые в точках .

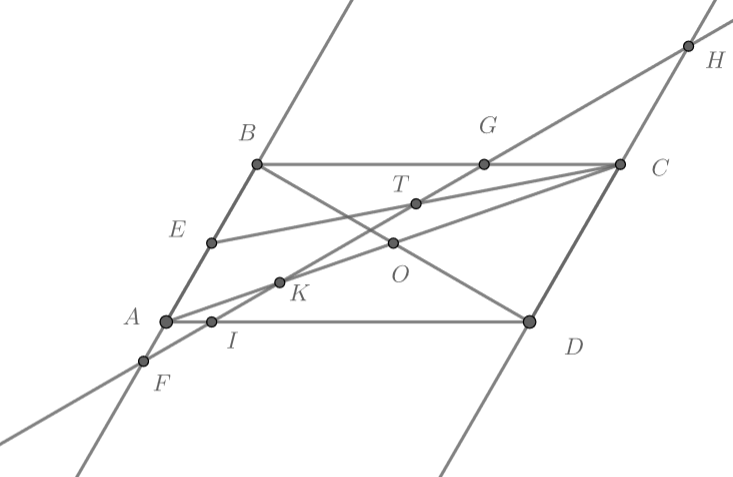
Из теоремы Менелая для треугольника получаем, что

Так как , то .

Далее замечаем, что . Тогда

Откуда .

Из подобия получаем

То есть .

Аналогично из подобия получаем

То есть .

Проведем , где - точка на . Тогда

И . Тогда из теоремы косинусов для треугольника получим .

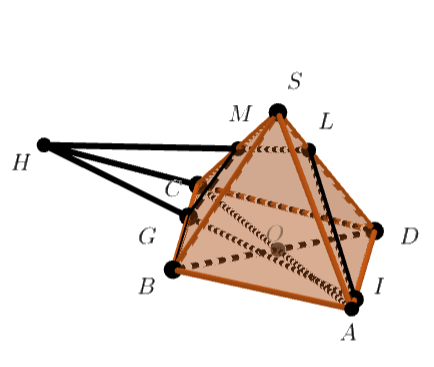
Пусть - точка, в которой прямая пересекает ребро . Тогда из теоремы Менелая для и прямой получим:

Далее из теоремы Менелая для имеем:

В силу параллельности прямых и имеем , откуда . По теореме косинусов для имеем , то есть . Из теоремы Пифагора для треугольника получаем , откуда . По теореме косинусов для имеем , а значит . По теореме Пифагора для вычислим . Заметим, что для треугольника выполняется теорема Пифагора, то есть угол прямой. С помощью теоремы косинусов для треугольника вычислим . Теперь через теоремы косинусов для треугольников и вычислим длины отрезков . Далее по теореме Герона получаем .

Заметим, что . Значит, .