Параметры на ШВБ

Упростим второе уравнение системы:

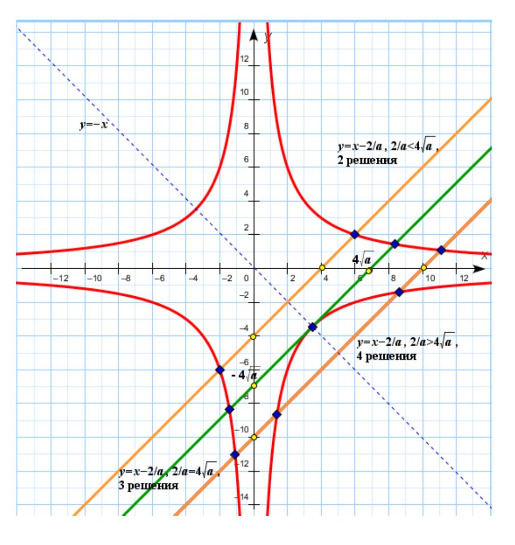
I.

1) Система имеет 2 различных решения, если

Найдем эти решения:

2) Система имеет 3 различных решения, если

Найдем эти решения:

3) Система имеет 4 различных решения, если

Найдем эти решения:

II.

при имеем при имеем

1) Система имеет 2 различных решения, если

Найдем эти решения:

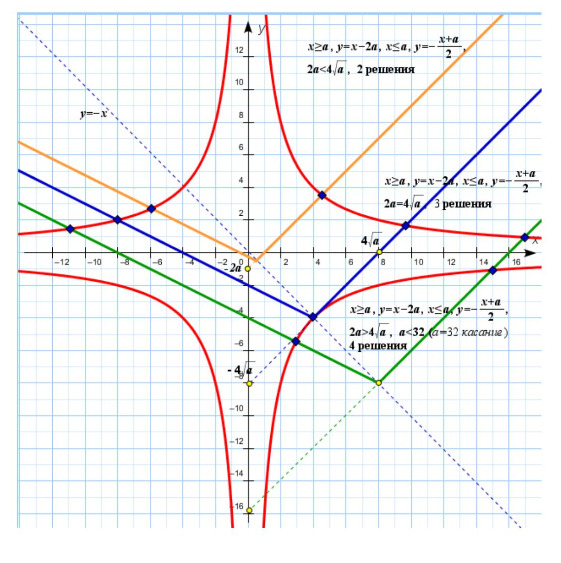
2) Система имеет 3 различных решения, если

Найдем эти решения:

3) Найдем значение параметра при котором прямая будет касаться графика гиперболы

Тогда при система будет иметь 4 решения:

Найдем четвертое решение:

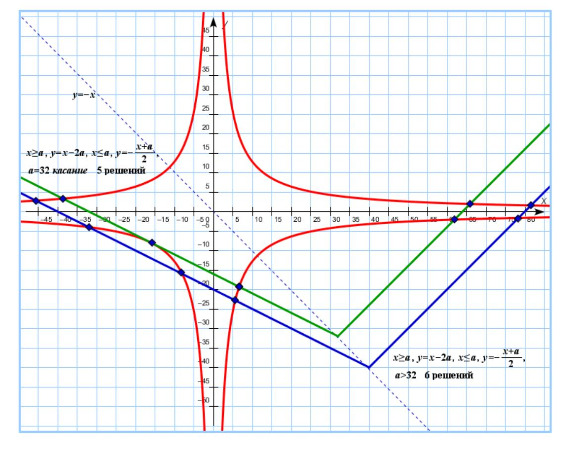
4) При система будет иметь 5 различных решений:

5) Система имеет 6 различных решений при :

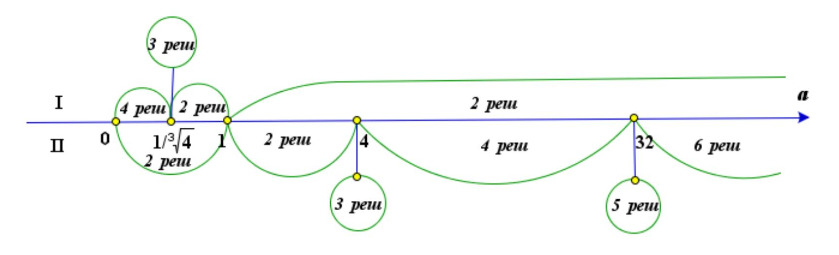
Возможны следующие случаи совпадения решений в I и II случаях:

1) в этом случае нет решений;

2) прямые и гипербола пересекаются в одной точке, но этот случай возможен при и в этом случае будет 7 решений.