Стереометрия на Звезде
Ошибка.
Попробуйте повторить позже
Параллелограмм является основанием пирамиды
Точки
и
лежат на рёбрах
и
соответственно,
причём
В каком отношении плоскость делит ребро
Источники:
Подсказка 1
Построить точку пересечения плоскости MNP и ребра SB сразу так сложно. Кажется, не хватает какой-нибудь точки на MP, чтобы провести через неё и N прямую, пересекающую ребро SB в искомой точке (пусть K).
Подсказка 2
Да это же точка, получаемая пересечение MP и SO, где SO — пересечение плоскостей BSD и ASC, назовём её Т. Точку ввели, а как она делит SO — не узнали. А хотелось бы, потому что её можно рассмотреть и для △ASC (а мы знаем про то как делят его стороны M и P), и для △BSD (содержащий интересующую нас точку K).
Подсказка 3
Отношение ST : NO можно найти, рассмотрев △ASC. А ещё же у нас есть отношение AO : OC (подумайте, чем является точка O для основания). Часто, когда мы видим отношения отрезков, хочется применить теорему Фалеса, только вот нам не хватает несколько параллельных прямых... Какие можно провести, чтобы использовать оба упомянутых отношения на сторонах SA и AC?
Подсказка 4
В предыдущей подсказке попробуйте провести прямые из A и O параллельно MP. С помощью теоремы Фалеса можно найти отношение ST : NO. Если Вы всё правильно посчитали, то не составит труда, используя уже упомянутую теорему, найти отношение SK : KB.
Пусть плоскости и
пересекаются по прямой
Рассмотрим треугольник
Пусть
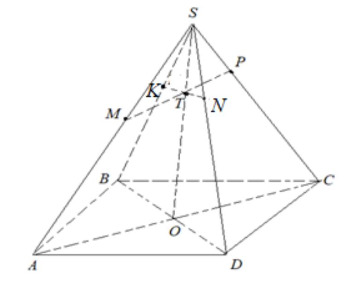
В треугольнике проведём прямые
и
параллельные
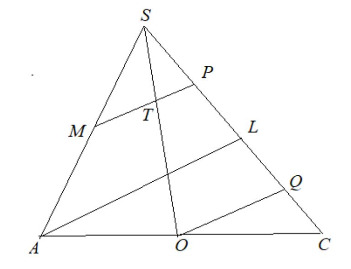
По теореме Фалеса имеем
Учитывая, что получаем, что
Пусть Так как
то в силу теоремы Фалеса прямые и
параллельны, и, следовательно,
Ошибка.
Попробуйте повторить позже
Боковые рёбра треугольной пирамиды попарно перпендикулярны, а стороны основания равны ,
,
. Центр сферы, которая
касается всех боковых граней, лежит на основании пирамиды. Найдите радиус этой сферы.
Источники:
Подсказка 1
Для начала, можно найти оставшиеся длины ребер: у нас же они перпендикулярны, а значит, можно применить теорему Пифагора!
Подсказка 2
С длинами разобрались, а что делать с радиусом вписанной сферы? На плоскости у нас есть полезный факт, что r = S/p, где S - площадь треугольника, а p - полупериметр. Если вы помните доказательство этого факта, то проведите аналогичные рассуждения здесь)
Подсказка 3
Если не помните, то сделайте вот что: вот у нас есть центр сферы O. Проведем отрезки из O ко всем вершинам пирамиды. Тогда он разбивается на 3 маленьких тетраэдра. Тогда его объем - сумма объемов маленьких тетраэдров. А чему равны объемы маленьких тетраэдров?)
Подсказка 4
А они равны 1/3 × r × (площадь грани). Причем площадь грани очень легко посчитать т.к. боковые ребра - перпендикулярны, и их длины мы знаем! Осталось ещё вспомнить формулу объема пирамиды у которой боковые ребра перпендикулярны, и дело в шляпе!
![]()
Обозначим основание пирамиды — , вершину пирамиды —
, центр сферы —
, радиус сферы —
. Пусть
. Обозначим
.
Так как радиус, проведённый в точку касания сферы и плоскости, ортогонален плоскости, имеем:
С другой стороны, так как боковые рёбра попарно перпендикулярны, то
Поэтому
Числа находятся из системы уравнений:
Складывая уравнения системы и деля на два, получим:
откуда . Тогда
Ошибка.
Попробуйте повторить позже
Плоскость, параллельная основанию пирамиды
, отсекает пирамиду
(вершины
расположены на
рёбрах
соответственно). Объём пирамиды
равен 375 , объём пирамиды
равен 81. Найдите объём
пирамиды
.
Источники:
Подсказка 1
Т.к. плоскости (A₁B₁C₁) и (ABC) параллельны, то MA₁/MA=MB₁/MB=MC₁/MC=k. Тогда объемы тетраэдров MA₁B₁C₁ и MABC относятся как коэффициент подобия k в кубе. Чему же равен k?
Подсказка 2
Верно, 3/5! Мы видим, что объем тетраэдра MAB₁C₁ состоит из объемов тетраэдров MA₁B₁C₁ и AA₁B₁C₁, у которых есть общее основание. Как же тогда относятся их объемы...
Подсказка 3
Они относятся как высоты, которые, в свою очередь, относятся как MA₁/A₁A=3/2. Посчитайте объем AA₁B₁C₁ и завершите решение!
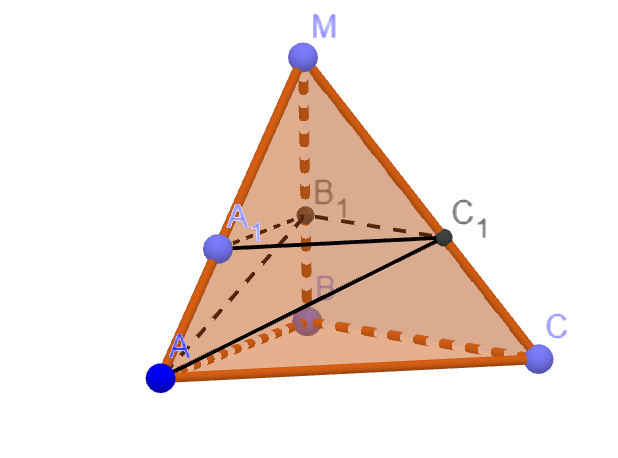
Так как плоскость параллельна плоскости основания
то
Пирамиды и
подобны, тогда их объёмы относятся как коэффициент подобия
в кубе:
Пусть тогда
Заметим, что объём пирамиды
складывается из двух кусочков:
объём
которой мы знаем, и
Причём эти 2 пирамиды имеют общее основание
тогда их объёмы относятся так же, как
относятся их высоты к
А высоты относятся так же, как относятся
и
то есть высота пирамиды
больше
высоты пирамиды
в
Значит,
Ошибка.
Попробуйте повторить позже
В правильной четырёхугольной пирамиде площадь основания совпадает с площадью боковой грани и равна
— точка
пересечения медиан грани
. Точка
лежит на прямой
и
Найдите сумму расстояний от точки
до всех
граней пирамиды.
Источники:
![]()
Из условия задачи сторона основания пирамиды равна , апофема боковой грани —
Тогда высота пирамиды
Объём пирамиды
равен
С другой стороны, объём пирамиды можно найти как сумму объёмов пяти пирамид, вершина которых — точка , а основания — грани
пирамиды
. Тогда
, где
— расстояния от точки
до граней пирамиды
(или высоты маленьких пирамид). Приравнивая объёмы, получаем
Заметим при этом, что сумма расстояний не зависит от расположения точки внутри данной пирамиды.



