Площадь сечения (+ построение сечений)
Ошибка.
Попробуйте повторить позже
Основанием пирамиды служит прямоугольный треугольник
с катетами
и
Высотой пирамиды
является отрезок
где точка
симметрична точке
относительно середины отрезка
Точка
принадлежит боковому ребру
причем
Найдите площадь сечения пирамиды плоскостью, проходящей через
параллельно гипотенузе основания
и отрезку
если расстояние от точки
до секущей плоскости равно
Источники:
Подсказка 1
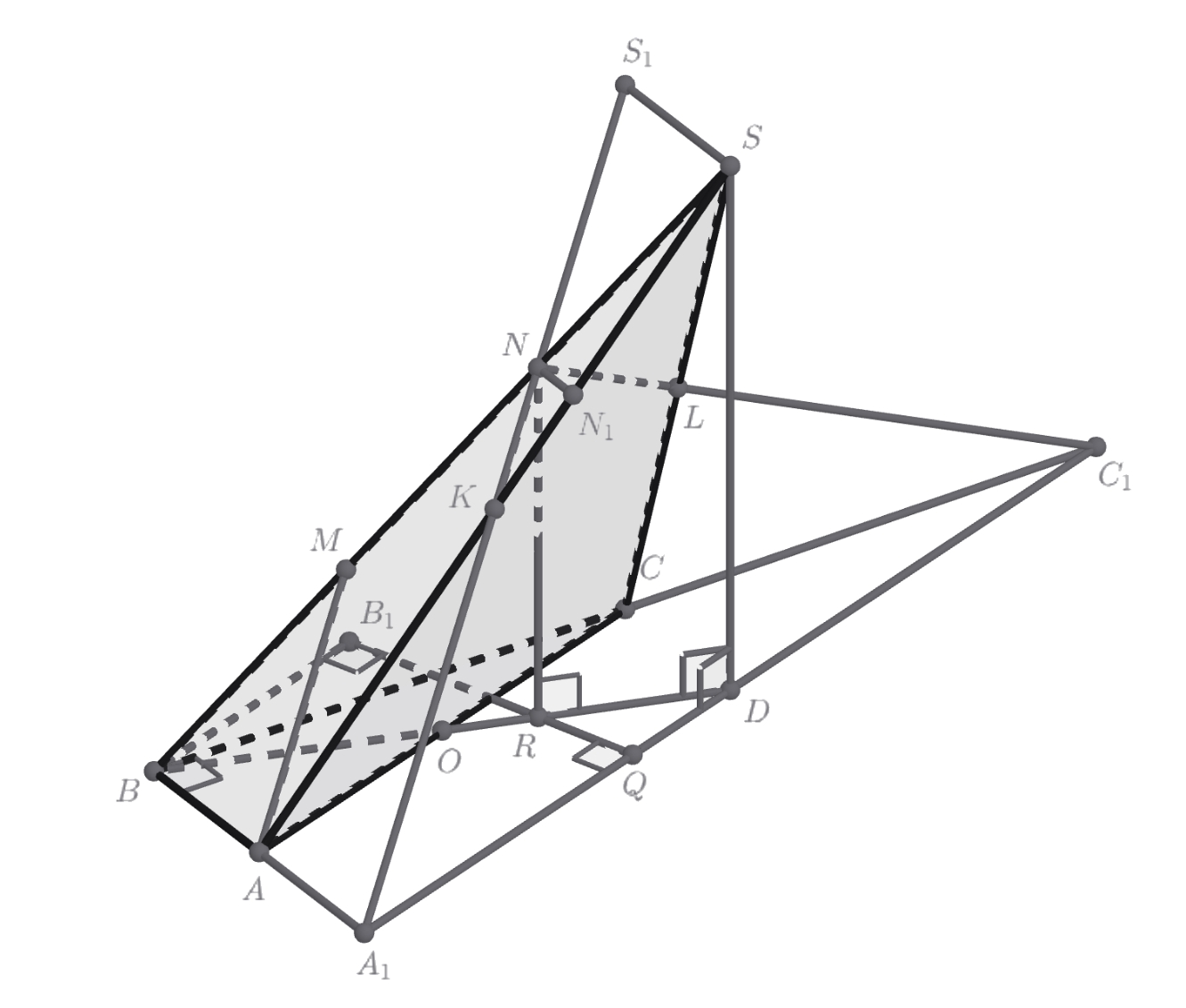
Если вы верно построили сечение, то оно должно быть треугольником. Обозначим его через KNL (K на AS, N на BS, L на CS). Пусть A₁ симметрична B относительно A, аналогично определим C₁. Заметим, что треугольники KNL и A₁NC₁ подобны.
Подсказка 2
Отметьте на BD такую точку R, что NR || SD. Тогда NR перпендикулярна плоскости основания. Также проведите через R Прямую, перпендикулярную A₁C₁ и пересекающую её в Q. Что можно сказать про NQ в треугольнике A₁NC₁?
Подсказка 3
Также давайте проведём через B прямую параллельно A₁C₁ и пересечём её с RQ в B₁. Расстояние от B до секущей плоскости равно расстоянию от B₁ до секущей плоскости (почему?). Дальше осталось аккуратно посчитать ответ.
Треугольник — прямоугольный,
точка
точка
симметрична
относительно
Секущая плоскость
проведена через точку
расстояние
от точки
до плоскости
Проведём через точку
прямую
параллельную
такую, что
Также отметим точку
на
такую, что
средняя линия
и
пересекает
в точке
Тогда
видим, продлив
до пересечения в точке
с прямой, проходящей через
паралелльно
и лежащей в плоскости
что
К тому же
Проведём через точку в плоскости
прямую, параллельную
и пересекающую
в точке
Тогда получаем,
что
Аналогично, проведя подобные рассуждения в плоскости получаем, что
где
точка пересечения
и
Плоскость
содержит
сечение — треугольник
Для площадей, в силу подобия треугольников, имеем соотношение
Отметим на
точку
такую, что
Тогда
Через
проведём прямую
и пусть она пересекает прямую, параллельную
и проходящую через
в точке
Тогда по теореме о
перпендикулярах
откуда
Найдем
Поскольку
и расстояние
от точки
до плоскости
равно расстоянию от точки
до
плоскости
Длина отрезка
равна высоте треугольника
Имеем Пусть
. Тогда
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




