Площадь сечения (+ построение сечений)
Ошибка.
Попробуйте повторить позже
Дана правильная четырехугольная пирамида с вершиной
, стороны основания которой равны
, а боковые ребра равны
Найдите площадь сечения пирамиды плоскостью, проходящей через точку
и середину ребра
параллельно прямой
.
Подсказка 1
Как нам переформулировать условие на то, что плоскость сечения параллельна BD? По какой прямой когда эта плоскость будет сечь плоскость BDS? Как при построения сечения нам поможет прямая по которой плоскость сечения пересекает BDS?
Подсказка 2
Да, эта плоскость сечет плоскость BDS по параллельной BD прямой! Значит, нам осталось найти одну точку пересечения плоскости сечения с плоскость BDS, и мы сможем построить прямую по которой плоскость сечения пересекает плоскость BDS(неопытный читатель спросит: «А зачем вообще нам искать эту прямую?». Дело в том, что если мы найдем эту прямую, то найдем по точке, которая принадлежит плоскости сечения и прямым SD и BD, а значит и плоскостям боковых граней. При этом у нас уже есть середина ребра. Так мы и построим сечение.) Осталось найти точку, как это сделать, зная, что трапеция правильная и что M лежит в плоскости сечения?
Подсказка 3
Правильно, в силу симметрии(пусть О-центр ABCD), SO и AM лежат в одной плоскости и пересекаются. И точка их пересечения, очевидно, лежит в плоскости сечения. Значит, мы нашли эту точку. Значит, и прямую, а значит построили сечение. Остается посчитать его площадь. Мы пользовались симметрией. А что еще она нам может сказать, скажем про четырехугольник, который является сечением пирамиды?
Подсказка 4
Верно, он дельтоид. Значит, его диагонали обладают некоторым свойством. Теперь посчитать площадь-дело техники, по нахождению длин диагоналей, не так ли? Конечно так, несколько подобий/теорем Фалеса и теорем Пифагора.
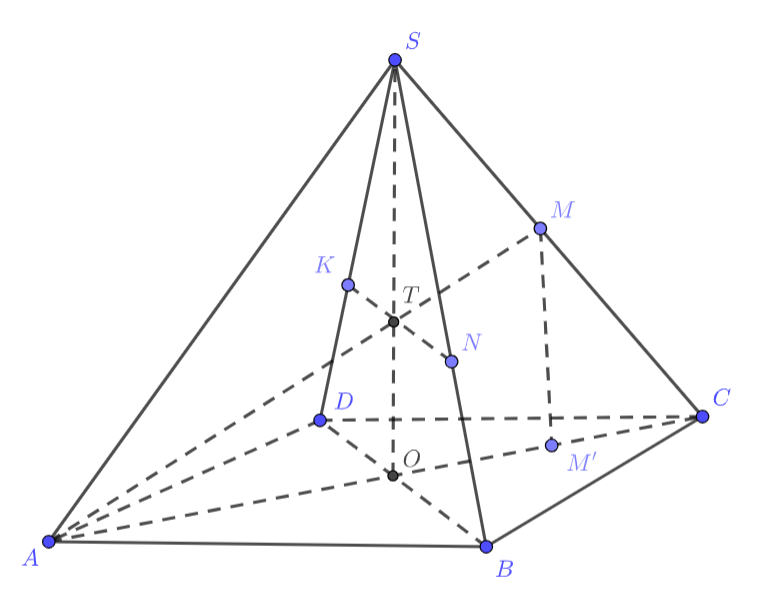
Пусть . Опустим высоту пирамиды в точку
— центр квадрата
. Далее пересечём
(все они
лежат в плоскости
), заметим, что
, откуда пересечение этой плоскостью нашей — прямая
, где
. Отсюда
будет искомым сечением.
В силу выполнено
, то есть площадь можно найти по формуле
. Далее
— центр
треугольника
, как пересечение двух медиан, то есть
Кроме того,
Отсюда , а по свойству точки пересечения медиан
. В итоге
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




