Площадь сечения (+ построение сечений)
Ошибка.
Попробуйте повторить позже
Основанием четырехугольной пирамиды является параллелограмм
со сторонами
и углом
,
равным
. Высотой пирамиды
является отрезок
, где
- точка пересечения диагоналей параллелограмма
. Найдите площадь сечения пирамиды
плоскостью, параллельной медиане
боковой грани
и
проходящей через середину ребра
и середину отрезка
.
Источники:
Подсказка 1
То, что в условии нам даны все длины, может подтолкнуть к тому, что это очень техническая задача. Здесь придется много считать и не бояться больших и страшных дробей. Первым делом нужно построить сечение. Поищите точку, принадлежащую сечению, на плоскости ABCD.
Подсказка 2
Теперь рассмотрим саму плоскость ABCD. У нас есть прямая, лежащая в этой плоскости и принадлежащая сечению. Где эта прямая пересекает прямые, содержащие стороны параллелограмма ABCD? Найдите отношения с помощью теоремы Менелая и подобия.
Подсказка 3
Пусть эта прямая пересекает прямые AB,BC,CD, AD в точках F,G,H,I соответственно. Пусть L - точка, в которой прямая HM пересекает ребро SD. Тогда искомое сечение это LMGI. Найдем его площадь как разность площадей треугольников LHI и MGH. А как найти их площади? Много считать длины сторон и отношения, используя теоремы Менелая, Герона, Пифагора, косинусов.
Пусть — середина ребра
а точка
- середина отрезка
. Рассмотрим плоскость
. Так как плоскость сечения
параллельна медиане
и проходит через точку
, построим прямую
в плоскости
. Тогда
- средняя линия в
, а
середина
.
Теперь нам известны три точки сечения: . Рассмотрим основание пирамиды
и посмотрим, как прямая
пересекает
стороны основания. Пусть эта прямая пересекает прямые
в точках
.
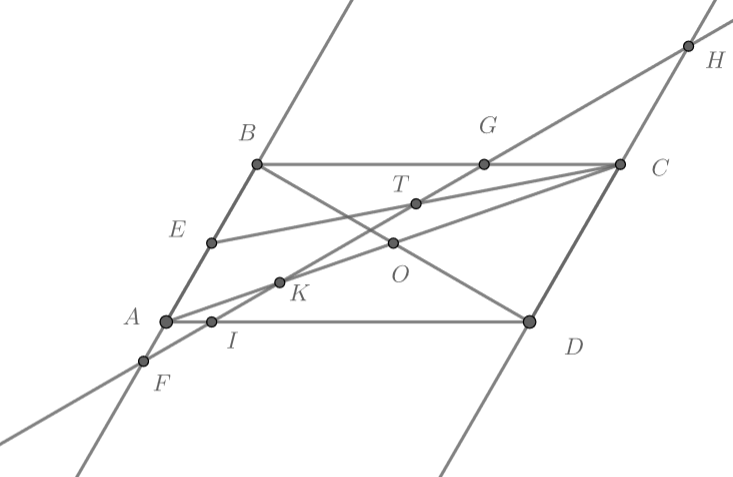
Из теоремы Менелая для треугольника получаем, что
Так как , то
.
Далее замечаем, что . Тогда
Откуда .
Из подобия получаем
То есть .
Аналогично из подобия получаем
То есть .
Проведем , где
- точка на
. Тогда
И . Тогда из теоремы косинусов для треугольника
получим
.
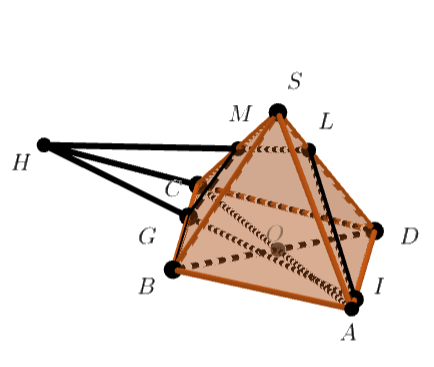
Пусть - точка, в которой прямая
пересекает ребро
. Тогда из теоремы Менелая для
и прямой
получим:
Далее из теоремы Менелая для имеем:
В силу параллельности прямых и
имеем
, откуда
. По теореме косинусов для
имеем
, то есть
. Из теоремы Пифагора для треугольника
получаем
, откуда
. По теореме косинусов для
имеем
, а значит
. По теореме Пифагора для
вычислим
. Заметим, что для треугольника
выполняется теорема Пифагора, то есть угол
прямой.
С помощью теоремы косинусов для треугольника
вычислим
. Теперь через теоремы косинусов
для треугольников
и
вычислим длины отрезков
. Далее по теореме Герона получаем
.
Заметим, что . Значит,
.
Ошибка.
Попробуйте повторить позже
![]()
Построим прямую, проходящую через точку параллельную
![]()
Тогда:
Построим пересечение плоскости и прямой
По теореме Менелая найдем, где
пересекает отрезок
![]()
Чтобы найти сечение, проходящее через точку воспользуемся гомотетией. Для этого найдем отношение
![]()
Точка перейдет в точку
точка
перейдет в точку
точка
перейдет в точку
Соответственно
—
как следствие гомотетии, а
— по теореме Менелая. Получается что нужное нам сечение —
а отношения в которых
данная точка пересекает ребра тетраэдара:
Ошибка.
Попробуйте повторить позже
Через середину бокового ребра правильной треугольной пирамиды проведено сечение, параллельное двум скрещивающимся ребрам этой
пирамиды. Найдите площадь этого сечения, если сторона основания равна , а боковое ребро равно
Пусть — правильная пирамида, а сечение проходит через середину
. В силу симметрии можно утверждать, что оно параллельно
и
. Итак,
— середина
,
— плоскость сечения, тогда в силу её параллельности
выполнено
, где
—
середина
. Далее, если
— высота основания, а
— её середина, то
, поскольку в силу параллельности
в
лежит
вся средняя линия
(
) треугольника
. Осталось снова воспользоваться
, откуда вся средняя линия
(
) треугольника
лежит в
, то есть
— сечение (построение сечения стандартно, как на ЕГЭ, но требует
обоснований).
Итак, , а также
как средние линии, следовательно,
— параллелограмм,
— его высота,
, так что
.
![]()
Ошибка.
Попробуйте повторить позже
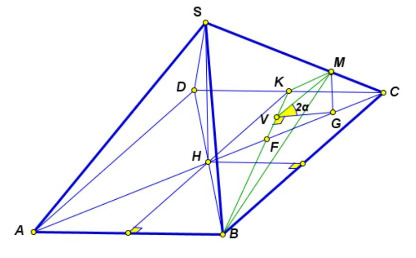
Найдите площадь сечения правильной шестиугольной пирамиды плоскостью, проходящей через вершину
основания
и параллельной медиане
боковой грани
и апофеме
боковой грани
если сторона основания пирамиды
равна
а расстояние от вершины
до секущей плоскости равно
Источники:
Подсказка 1
Итак, перед нами стереометрия с ШВБ, технической олимпиады, а значит придётся много считать и не бояться этого. Но для того, чтобы найти площадь сечения, нужно сначала его построить, что не очень просто, ведь пирамида аж шестиугольная. Однако нам дано целых две прямые, параллельные сечению, поэтому, хорошей идеей для начала решения будет постpоение разных прямых, параллельных данным в некоторых плоскостях.
Подсказка 2
Построим прямую SQ, параллельную CM, точка Q принадлежит CD. Что теперь можно сказать про отношение плоскостей SQN и сечения?
Подсказка 3
Они параллельны! Через точку F проведём прямую, параллельную NQ, пусть она пересекает CD в точкe V. Правда ли, что эта прямая принадлежит сечению?
Подсказка 4
Да, это верно! Через точку V проведем прямую VL, параллельную CM, L лежит на SC. Получается, плоскость FVL — плоскость сечения. Теперь нетрудно найти точки, в которых эта плоскость пересекает плоскость пирамиды.
Подсказка 5
Ура, мы построили сечение! Но получился пятиугольник, как теперь искать его площадь? Вспомните формулу: Площадь сечения равна площади проекции сечения на основание делить на угол между плоскостями сечения и основания.
Подсказка 6
Дальше дело техники! Площадь проекции найдите как сумму площадей треугольников. Длины различных отрезков можно искать и выражать через длину стороны основания с помощью подобия, теоремы Фалеcа. Не забывайте так же про большое количество параллельных прямых на чертеже и правильность шестиугольника в основании. А для того, чтобы найти угол, нужно вспомнить про данное в условии расстояние!
Построим сечение пирамиды. В плоскости через точку
проведем прямую
параллельную
принадлежит прямой
Тогда
будет средней линией треугольника
следовательно,
где
— сторона основания
пирамиды.
Плоскость содержит прямые
и
которые параллельны плоскости сечения, следовательно, по признаку плоскость
параллельна плоскости сечения.
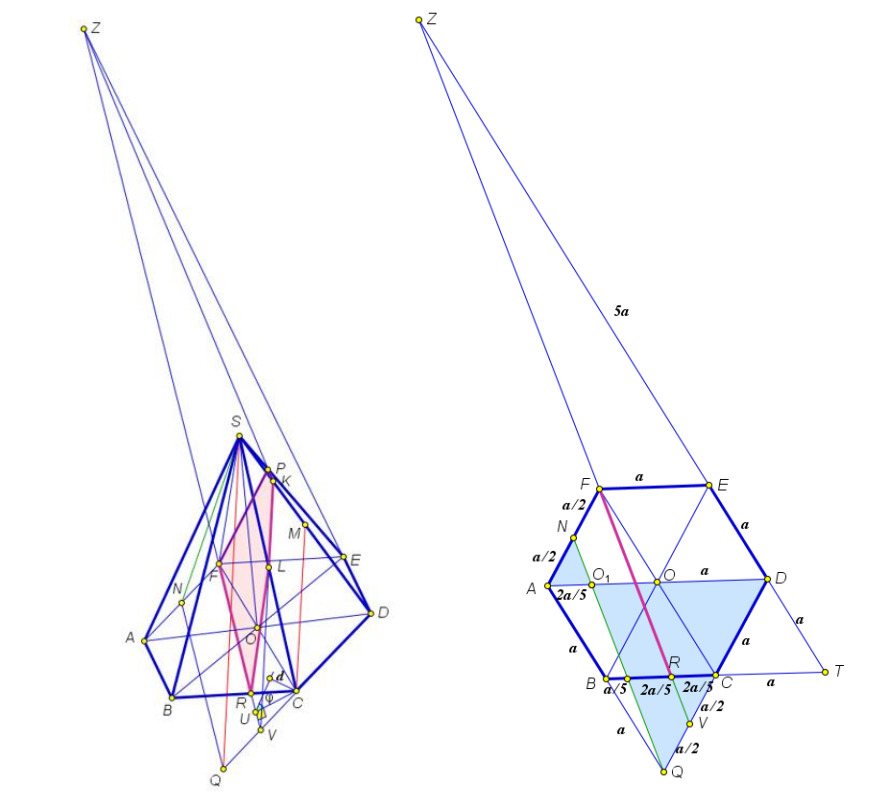
Через точку проведем прямую
параллельную
где
принадлежит прямой
Т.к.
и
значит,
— параллелограмм, следовательно,
Учитывая, что
— середина
а также
можем
сказать, что
Пусть — точка пересечения прямых
и
Плоскость сечения пересекает основание пирамиды по отрезку
Пусть — точка пересечения
и
Заметим, что углы
И
равны как вертикальные, а углы
и
как накрестлежащие при параллельных прямых
и
и секущей
Следовательно, треугольники
и
подобны,
поэтому
Т.к. является правильным шестиугольником, значит,
Учитывая, что
получаем,
что
Т.к.
и
углы
и
равны, аналогично, т.к.
и
углы
и
равны, а также
следовательно, треугольники
и
равны, поэтому
Пусть точка — точка пересечения прямых
и
а точка
— точка пересечения прямых
и
Из-за того, что
— правильный шестиугольник, можно сделать вывод, что
Т.к.
треугольники
и
подобны, поэтому
В плоскости через точку
проведем прямую
параллельную
принадлежит ребру
— точка пересечения
прямой
с ребром
параллельны друг другу, поэтому по теореме Фалеса имеем
В плоскости точка
— точка пересечения прямых
и
Запишем теорему Менелая для треугольника
и секущей
Искомое сечение - это Для нахождения площади сечения используем формулу
где — площадь проекции сечения на плоскость основания,
— угол между плоскостью сечения и плоскостью основания. Найдем
площадь проекции сечения на плоскость основания.
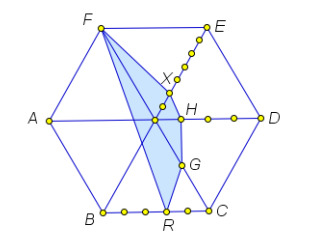
Проекцией является пятиугольник Площадь проекции сечения вычисляется по формуле
Обозначим расстояние от точки до плоскости сечения
Т.к. точка
принадлежащая плоскости сечения является
серединой
расстояние от точки
до сечения тоже равно
В треугольнике
проведем высоту
обозначим ее длину
Тогда
Т.к. — правильный,
Тогда найдем
по теореме косинусов:
Используя различные формулы для нахождения площади треугольника имеем
Тогда
Окончательно имеем
Ошибка.
Попробуйте повторить позже
Дан куб с ребром 1, нижним основанием и боковыми ребрами
. На ребрах
отмечены
соответственно точки
, так что
,
,
. Найдите площадь сечения
тетраэдра
, параллельного ребрам
и
, имеющего форму ромба.
Источники:
Подсказка 1
Начнём с хорошего чертежа! Возможно, будет удобно отдельно вынести тетраэдр KLMN, чтобы удобнее было работать с сечением. В каком случае сечение тетраэдра будет ромбом? А что нам нужно, чтобы найти его площадь?
Подсказка 2
Будем вычислять стороны ромба и угол между ними. Заметим также, что этот угол равен углу между рёбрами KL и MN тетраэдра. Итак, пусть вершина ромба делит ребро KN в отношении х/у, что можно сказать о том, в каких отношениях вершины ромба делят другие рёбра тетраэдра? Параллельность нам поможет это установить!
Подсказка 3
При помощи теоремы Пифагора можно вычислить любое ребро тетраэдра. А подобие треугольников поможет нам после этого отыскать сторону ромба. Но как же найти угол?
Подсказка 4
KL и MN, а также другие пары параллельных им прямых, не выглядят удобными для построения угла между прямыми напрямую, однако куб — очень хорошая фигура для работы с декартовой системой координат! Введите координаты и при помощи работы с векторами определите искомый угол. Остаётся лишь подставить найденные значения в формулу площади ромба и задача убита!
Пусть — длина стороны ромба,
— его меньший угол. Тогда искомая площадь равна
причем угол
равен углу между
прямыми
и
т.к. сечение параллельно ребрам
и
![]()
Найдем Пусть сечение пересекает стороны
в точках
соответственно. Тогда
и
Пусть
и
имеют длину
и
соответственно. По теореме о пропорциональных отрезках для параллельных прямых
и
понимаем, что
Из подобия треугольников и
и треугольников
и
получаем
Отсюда то есть
По теореме Пифагора
Отсюда
Найдем угол — угол между
и
Он равен углу между направляющими для этих прямых векторами
и
Их скалярное произведение равно
Следовательно,
Соответственно,
Значит, искомая площадь равна
Ошибка.
Попробуйте повторить позже
Пересечение плоскости и правильной треугольной пирамиды является квадратом со стороной 1. Найдите длину ребра
основания пирамиды, если известно, что двугранный угол между плоскостью боковой грани и плоскостью основания равен
Источники:
Подсказка 1
Пусть исходная пирамида — SABC, SA = b. AB = a. Знание о том, что пирамида правильная, помогает нам понять, куда упадёт высота этой пирамиды, а значит — построить косинус двугранного угла. В каком случае сечение будет квадратом, как связаны его стороны с рёбрами пирамиды?
Подсказка 2
Выразите через а и b все отрезки, необходимые для нахождения косинуса, после этого можно будет установить связь между a и b. А как нам определить отношение стороны квадрата к ребру а?
Подсказка 3
Пусть вершина квадрата-сечения делит ребро АВ в отношении m/n, в каком отношении делится ребро SB этим же сечением? При помощи подобия треугольников и известного отношения a/b установите численно отношение m/n. После этого, подстановкой известных отношений, вычислите а.
Поскольку сечение — четырёхугольник, плоскость пересекает все грани. Обозначим вершшины основания через и вершину
пирамиды через
. Тогда можно считать, что секущая плоскость пересекает рёбра
в точках
соответственно.
Поскольку
, прямая
параллельна всей плоскости
. Стало быть,
. Аналогично,
. Положим
.
![]()
Тогда косинус двугранного угла при основании равен
что по условию равно , откуда
. Из того, что
получаем:
Таким образом,
то есть .
Ошибка.
Попробуйте повторить позже
Дана правильная четырехугольная пирамида с вершиной
, стороны основания которой равны
, а боковые ребра равны
Найдите площадь сечения пирамиды плоскостью, проходящей через точку
и середину ребра
параллельно прямой
.
Подсказка 1
Как нам переформулировать условие на то, что плоскость сечения параллельна BD? По какой прямой когда эта плоскость будет сечь плоскость BDS? Как при построения сечения нам поможет прямая по которой плоскость сечения пересекает BDS?
Подсказка 2
Да, эта плоскость сечет плоскость BDS по параллельной BD прямой! Значит, нам осталось найти одну точку пересечения плоскости сечения с плоскость BDS, и мы сможем построить прямую по которой плоскость сечения пересекает плоскость BDS(неопытный читатель спросит: «А зачем вообще нам искать эту прямую?». Дело в том, что если мы найдем эту прямую, то найдем по точке, которая принадлежит плоскости сечения и прямым SD и BD, а значит и плоскостям боковых граней. При этом у нас уже есть середина ребра. Так мы и построим сечение.) Осталось найти точку, как это сделать, зная, что трапеция правильная и что M лежит в плоскости сечения?
Подсказка 3
Правильно, в силу симметрии(пусть О-центр ABCD), SO и AM лежат в одной плоскости и пересекаются. И точка их пересечения, очевидно, лежит в плоскости сечения. Значит, мы нашли эту точку. Значит, и прямую, а значит построили сечение. Остается посчитать его площадь. Мы пользовались симметрией. А что еще она нам может сказать, скажем про четырехугольник, который является сечением пирамиды?
Подсказка 4
Верно, он дельтоид. Значит, его диагонали обладают некоторым свойством. Теперь посчитать площадь-дело техники, по нахождению длин диагоналей, не так ли? Конечно так, несколько подобий/теорем Фалеса и теорем Пифагора.
Пусть . Опустим высоту пирамиды в точку
— центр квадрата
. Далее пересечём
(все они
лежат в плоскости
), заметим, что
, откуда пересечение этой плоскостью нашей — прямая
, где
. Отсюда
будет искомым сечением.
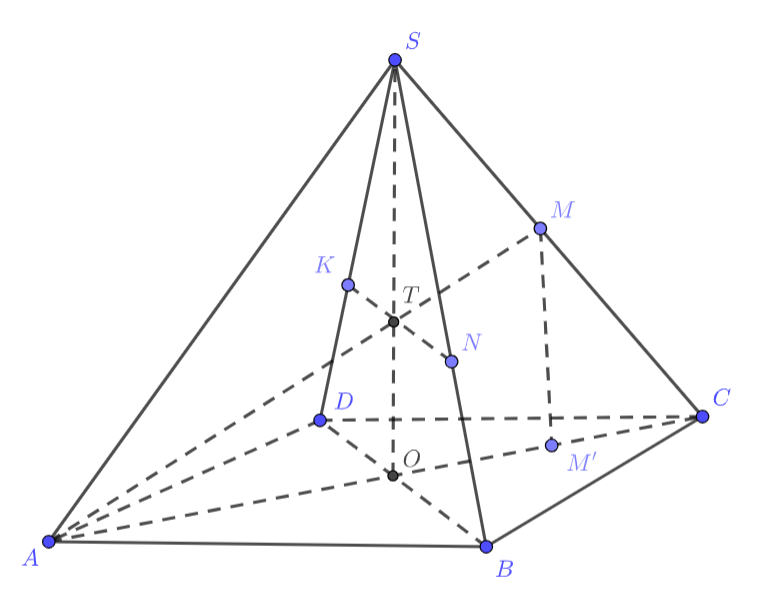
В силу выполнено
, то есть площадь можно найти по формуле
. Далее
— центр
треугольника
, как пересечение двух медиан, то есть
Кроме того,
Отсюда , а по свойству точки пересечения медиан
. В итоге
Ошибка.
Попробуйте повторить позже
Объём правильной четырёхугольной пирамиды равен , угол между боковым ребром и плоскостью основания равен
.
Рассматриваются правильные треугольные призмы, вписанные в пирамиду так, что одно из боковых рёбер лежит на диагонали основания
пирамиды, одна из боковых граней параллельна основанию пирамиды, и вершины этой грани лежат на боковых гранях
пирамиды. Найдите объём той призмы, плоскость боковой грани которой делит высоту пирамиды в отношении
, считая от
вершины.
Обозначим через сторону основания
данной пирамиды
.
Пусть плоскость, параллельная основанию пирамиды и проходящая через точку лежащую на высоте пирамиды, делит высоту в
данном отношении
. Тогда в сечении пирамиды этой плоскостью получится квадрат
со стороной
(
).
Пусть боковое ребро правильной призмы
лежит на диагонали
квадрата
. Тогда вершины
противоположной грани
лежат на сторонах соответственно
квадрата
.
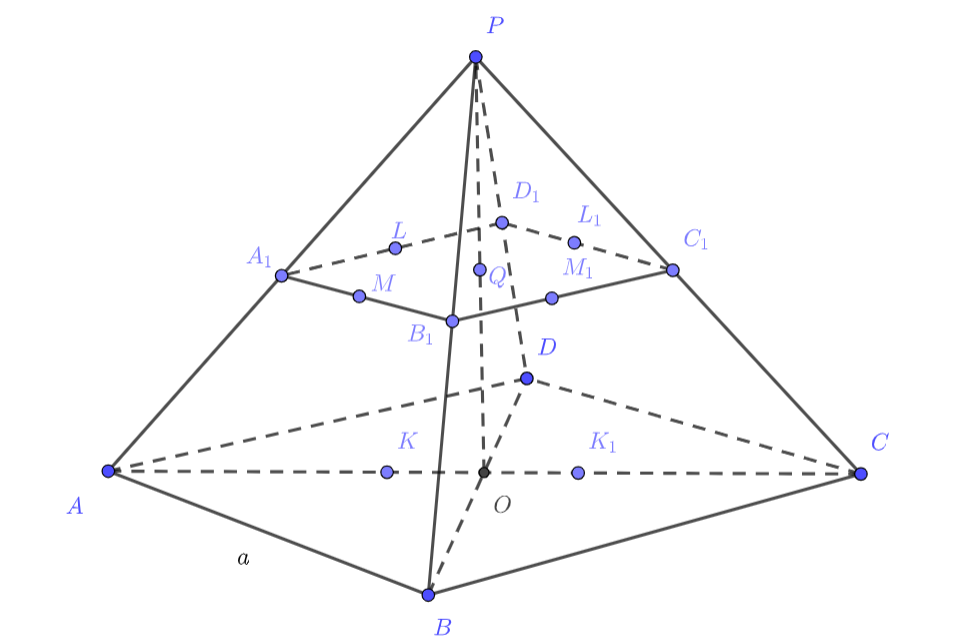
Из прямоугольного треугольника находим, что
Тогда если - высота равностороннего треугольника
, то
Пусть - сторона основания призмы. Тогда
. Из уравнения
находим, что
.
Обозначим . Поскольку прямоугольник
вписан в квадрат
, причём его стороны
параллельны диагоналям квадрата, то периметр прямоугольника равен сумме диагоналей квадрата, т. е.
.
Значит,
Поэтому
Выразим найденный объём через объём данной пирамиды:
Следовательно,
Ошибка.
Попробуйте повторить позже
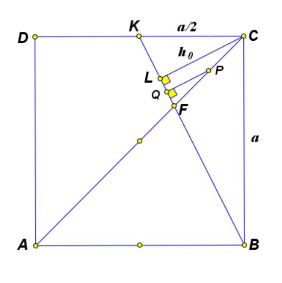
Шар радиуса лежит внутри правильной четырехугольной пирамиды
со стороной основания 8 и высотой 3.
Этот шар касается плоскости основания
пирамиды и боковых граней
и
Плоскость
касается
шара, проходит через точку
середину
ребра
и пересекает ребро
в точке
Найдите объем пирамиды
Подсказка 1.
Сразу же введём основание высоты пирамиды (например, через точку H) и центр шара (например, через точку O). Раз в условии у нас правильная пирамида, то центр данного шара лежит в плоскости SHC. Тогда удобно будет провести прямую, проходящую через центр O параллельно SH (пусть это прямая PR). Мы сразу знаем OP, ведь он равен радиусу, а также то, что RP перпендикулярен плоскости основания пирамиды. Введём коэффициент подобия треугольников SCH и RCP (пусть он равен 1/k). Тогда, зная SH, мы можем выразить PR через k. Хорошо бы было выразить ещё отрезки через k, чтобы впоследствии прийти к уравнению и найти k. Попробуйте сделать это в плоскости ABCD.
Подсказка 2.
В плоскости ABCD мы можем провести прямую, проходящую через P параллельно AB. Пусть она пересекает BC в точке N. Тогда, так как ABCD — квадрат, то AH = HC, и с помощью этого мы легко можем выразить PN через AB и k. Теперь можно заметить, что точка касания шара и плоскости SBC лежит на RN. Что тогда мы можем сказать про треугольники ROE и RPN?
Подсказка 3.
Верно, они подобны. Тогда, записав подобие, мы можем получить уравнение на k, откуда k = 1/3. Отлично, теперь пора возвращаться к плоскости из условия. Чтобы найти объём MBCK, нужно найти высоту из M на BCK (пусть это отрезок MG) и площадь треугольника BCK. С треугольником BCK нет никаких проблем, ведь мы знаем сторону квадрата ABCD и отношение CK к KD, а значит, можем найти любой элемент треугольника. Но как же найти MG? Попробуйте выразить его через SH и коэффициент подобия треугольников MCG и SCH (пусть он равен n). Чтобы найти n, можно использовать угол между плоскостями MKB и KBC, опустив высоту GV на BK.
Подсказка 4.
Используя подобие треугольников VFG и FKC (F является точкой пересечения BK и AC), мы можем выразить GV через n. Тогда мы можем выразить тангенс угла MVG через n. Отлично! Теперь осталось лишь найти этот угол. Мы знаем, что он является линейным углом двугранного угла между плоскостями MKB и KBC. Для решения задачи мы ещё не использовали, что плоскость MKB касается шара (пусть точка касания — точка T). Зная это, мы можем опустить перпендикуляр PQ на BK и получить, что TQP также является линейным углом двугранного угла между плоскостями MKB и KBC. Теперь нужно найти угол TQP. Его не очень удобно искать, однако посмотрите на треугольники OTQ и OQP. Попробуйте найти угол, используя их равенство.
Подсказка 5.
Треугольники OTQ и OQP равны, а значит и углы TQO и OQP. Тогда угол TQP в два раза больше угла OQP. А вот угол OQP легко найти, ведь мы можем выразить PQ через подобие треугольников QFP и KFC, а OP мы знаем. Так мы найдём тангенс угла OQP. Затем по формуле тангенса двойного угла найдём тангенс угла TQP и, подставив в уравнение, найдём n. Осталось лишь подставить n в формулу MG и найти объём.
Поскольку пирамида правильная, то центр
указанного шара лежит в плоскости
, где
— высота пирамиды. Пусть
Обозначим Проведем
— точка касания шара плоскости
пусть радиус шара
Поскольку
то
Треугольники
и
подобны, и
или
По условию задачи Тогда
Точка — точка пересечения
и
тогда
Поскольку
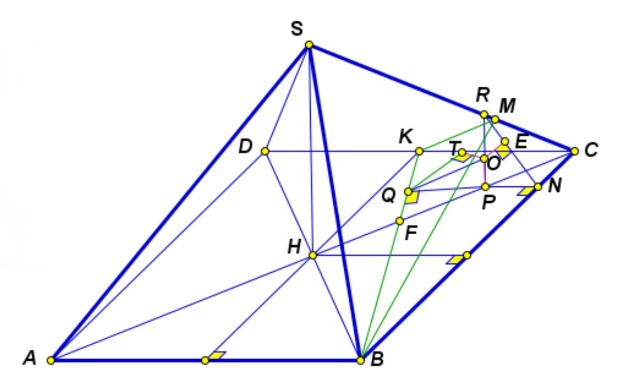
Пусть . Тогда
Если
то
Угол между плоскостью
и плоскостью основания
равен
Тогда
Пусть — отрезок перпендикуляра, опущенного из точки
на плоскость основания
, и
. Тогда
. Если
, то
— высота треугольника
проведенная из вершины
Ошибка.
Попробуйте повторить позже
В кубе , все рёбра которого равны единице, точка
— середина ребра
, точка
— центр грани
.
Множество точек, лежащих на грани
, таково, что для любой точки
этого множества плоскость
пересекает ребро
. Найдите площадь этого множества.
Источники:
Подсказка 1
Неудобно рассматривать какой-то произвольный случай для точки X. Тогда попробуйте рассмотреть граничные случаи (когда XOM пересекает ребро AD в точке A или D).
Подсказка 2
Для точки A всё ясно. В этом случае плоскостью XOM будет являться плоскость B₁AM. Теперь посмотрим на случай с точкой D. Прямые OD и B₁C₁ лежат в одной плоскости. Тогда что можно сказать про их взаимное расположение?
Подсказка 3
Точно! Они пересекаются (пусть в точке E). Теперь рассмотрим произвольную точку X нашего множества. Пусть она пересекает AD в точке F, а OF пересекает AD в точке G. Раз X лежит и в BB₁C₁C, и в FOM, то на какой прямой лежит эта точка?
Подсказка 4
Верно! На MG. Значит, наше множество представляется всеми такими прямыми MG. Но все они заключены между ME и MB₁. И раз X лежит на грани BB₁C₁C, то X лежит в той части треугольника MEB₁, что находится на грани BB₁C₁C. Тогда нам всего лишь осталось найти её площадь.
Подсказка 5
Необходимо найти площадь треугольника MHB₁ (H является точкой пересечения BB₁ и ME). То есть нужно вычислить значение 1/2×B₁H×C₁B₁. Осталось всего лишь найти B₁H. Для этого посмотрите на треугольники EHB₁ и EMC₁. Что можно про них сказать?
Построим плоскость . Для этого найдём точку пересечения прямой
с плоскостью
. Очевидно, что это будет точка
.
Значит, сечение куба плоскостью
пересекает ребро
в точке
.
![]()
Построим плоскость . Для этого найдём точку пересечения прямой
с плоскостью
. Прямые
и
лежат в
плоскости
, а
, значит,
пересекает
. Обозначим их точку пересечения через
, она также лежит в
плоскости DOM. Прямая
также лежит в плоскости
и пересекает ребро
в некоторой точке
. Заметим, что
треугольники
и
равны, значит,
. Треугольники
и
подобны с коэффициентом 2 , значит,
. Пусть
- некоторая точка искомого множества и плоскость
пересекает ребро
в точке
. Прямая
лежит в плоскости
, а значит, точка пересечения
прямой
с плоскостью
лежит на отрезке
. Прямая
лежит в плоскости
, причём она заключена между прямыми
и
. Поскольку точка
лежит в плоскостях
и
, то она лежит на прямой
, а следовательно, внутри треугольника
, значит, треугольник
— искомое
множество.
Ошибка.
Попробуйте повторить позже
Найдите площадь сечения правильной треугольной призмы плоскостью, которая параллельна диагонали
боковой грани
проходит через середину стороны
основания
и точку
лежащую на стороне
если,
расстояние между
и секущей плоскостью равно
а сторона основания призмы равна
В плоскости основания проводим прямую
параллельную
,
, и прямую
параллельную
лежит
в плоскости сечения. В плоскости основания
проводим прямую, соединяюшую точку
с серединой
стороны
,
точка
— точка пересечения этой прямой со стороной
. В плоскости основания
проводим прямую
,
параллельную
Точка
— точка пересечения прямой
со стороной
. Трапеция
— искомое
сечение.
Найдём площадь проекции сечения на плоскость основания призмы. Обозначим сторону основания через . Тогда
.
Пусть
— проекция точки
на основание
. Пусть
— проекция точки
на основание
. Поскольку
и
параллельны, то
, и
. Проекцией сечения на плоскость основания
является трапеция
, её
площадь
Найдём косинус угла наклона плоскости сечения к плоскости основания призмы. Расстояние
от прямой
до плоскости
сечения равно расстоянию от точки
до плоскости сечения, которое, в свою очередь, равно расстоянию от точки
до плоскости сечения
(
, где
принадлежит плоскости сечения).
Строим плоскость , проходящую через точку
и перпендикулярную
линии пересечения основания и плоскости сечения (
и
перпендикулярны
). Проведем прямую
перпендикулярную
, расстояние
равно
. Угол наклона плоскости
сечения к плоскости основания равен углу
. Находим:
В треугольнике имеем
Итого:
Ошибка.
Попробуйте повторить позже
Рассматриваются плоские сечения правильной пирамиды , параллельные боковому ребру
и диагонали основания
, в которые можно вписать окружность. Какие значения может принимать радиус этих окружностей, если
,
Источники:
Подсказка 1
В этой задаче условие может выглядеть очнеь страшно, поэтому первым делом нужно нарисовать аккуратный чертеж, чтобы понять, с какими объектами мы работаем. Теперь давайте подумаем, нам дана правильная пирамида (какой вывод можно сделать про ее основание?), мы знаем сторону и один из углов. Попробуем найти длины полезных отрезков в этой пирамиде. Например, с помощью косинуса SBD и длины OB (O - центр основания) можно найти SB - боковое ребро пирамиды!
Подсказка 2
Итак, вспомним, что это можно сделать, опустив высоту из S и заметив, что SOB - прямоугольный треугольник с известным нам катетом и углом. Итак, мы нашли длину боковой стороны, а теперь подумаем про сечения. Если вы нарисовали чертеж - подумайте, какие вообще варианты сечений у нас могут получаться? (вряд ли сечением пирамиды будет двенадцатиугольник, например). Затем попробуем рассмотреть каждый вид сечений отдельно.
Подсказка 3
Верно! У нас могут быть сечения всего двух видов - пятиугольные и треугольные! Мы знаем, что наше сечение пересекает плоскость основания по прямой A₁C₁, параллельной прямой AC. Обозначим за O- центр ABCD. Какое будет сечение, если прямая A₁C₁ лежит внутри треугольника ADC?
Подсказка 4
Верно! Это будет треугольник. Пускай S₁- его вершина, лежащая на ребре SD, а x- длина A₁C₁. Попробуйте найти S₁B₁ (выразить через х), где B₁- точка пересечения A₁C₁ и BD, если вы знаете, что S₁B₁ параллельна SB...
Подсказка 5
Площадь сечения должно получиться S₁B₁⋅A₁C₁/2=3x²/16. S₁C₁ можно найти из теоремы Пифагора. Воспользуйтесь тем, что r=S/p для оценки радиуса. А какое сечение будет, если A₁C₁ лежит внутри треугольника ACB?
Подсказка 6
Домик). Переобозначим A₁C₁ за A₂C₂=x, A₃- точка пересечения сечения и AS, C₃- сечения и SC, Q- сечения и SD, B₃- сечения и BD. Из того, что A₂A₃ и C₂C₃ параллельны SB и A₂C₂ и A₃C₃ параллельны AC, можно получить, что A₂A₃C₃C₂- параллелограмм, а т.к. SB перпендикулярен AC- прямоугольник. Попробуйте найти отрезки A₂A₃ и QA₃...
Подсказка 7
Если в наш пятиугольник можно вписать окружность, то будет верна формула S=pr. При этом мы знаем, что r=x/2, ведь наша окружность касается параллельных прямых A₂A₃ и C₂C₃, расстояние между которыми равно x. Осталось только посчитать площадь и полупериметр, и решить уравнение S=px/2
Так как пирамида правильная, то в основании лежит квадрат с диагоналями , пусть
— его центр. Тогда
является
высотой пирамиды, так что из условия про косинус находим
Плоскость сечения параллельна , поэтому содержит параллельную
прямую из плоскости
. Поэтому сечение может быть
двух видов:
![]()
1 случай) треугольник , где
лежит внутри
.
Тогда (строго меньше единицы, потому что сечение параллельно
, содержать
не может). Пусть
.
Теперь найдём, чему равняется (то есть радиус вписанной окружности)
![]()
2 случай) Пятиугольное сечение плоскостью , где
лежит внутри
. Заметим, что
и
поэтому
и
Пусть
Тогда из подобий и
получаем
Значит,
Также имеем
Откуда
Так как
. Тогда по теореме Пифагора
.
![]()
Воспользуемся формулой
Тогда
Ошибка.
Попробуйте повторить позже
В правильной четырёхугольной пирамиде сторона основания
равна
, высота
равна
Точка
лежит на
высоте
, причём
. Через точку
проведена плоскость
, перпендикулярная прямой
. Найдите
площадь сечения пирамиды плоскостью
, расстояние от точки
до плоскости
и угол между плоскостью
и прямой
.
Подсказка 1
Давайте начнём с поиска угла! Во-первых, давайте найдем, чему равны AO и AS - это можно сделать, исходя из условия, которое нам дано, и воспоминаний о теореме Пифагора. Если плоскость пересекает ребро AS в точке M, а ребро SD в точке P, то задачу можно переформулировать, как поиск угла SPM, а угол SMP мы знаем из перпендикулярности! Тогда как можно найти SPM?
Подсказка 2
SPM = 90 - MSP = 90 - ASD! Но мы знаем что-то про угол ASD - некоторые стороны в треугольнике, где он находится. Тогда мы можем узнать его синус!
Подсказка 3
Расстояние DP = DS - SP, а эти два расстояния попроще искать. DS мы уже знаем, а SP в треугольнике, где мы знаем угол, какие-то стороны можем тоже попробовать найти! Например, чтобы найти SP, попробуйте сначала найти SM и MP, чтобы вычислить расстояние
Подсказка 4
Площадь искомого треугольника можно найти, зная MN, MP и синус угла между ними. Попробуйте найти его, используя теорему косинусов! Для этого нам потребуются PM и PN, а значит надо найит PN (PM искали в прошлом пункте). А PN можно найти из теоремы косинусов в PNS!
Имеем . Пусть
. Тогда
Пусть плоскость П пересекается с прямыми и
в точках
и
соответственно.
![]()
В плоскости из прямоугольного
имеем
Далее из прямоугольного имеем
В плоскости из прямоугольного
имеем
Так как перпендикулярно плоскости
, то углом между прямой
и плоскостью
является
Так как
то расстояние от точки до плоскости
равно
В плоскости из
по теореме косинусов находим
Рассмотрим . Пусть
. Тогда по теореме косинусов получаем
Следовательно, , и искомая площадь сечения равна
Площадь равна
Расстояние равно
Угол равен



