Площадь сечения (+ построение сечений)

В плоскости основания проводим прямую параллельную , , и прямую параллельную лежит в плоскости сечения. В плоскости основания проводим прямую, соединяющую точку с серединой стороны , точка — точка пересечения этой прямой со стороной . В плоскости основания проводим прямую , параллельную Точка — точка пересечения прямой со стороной Трапеция — искомое сечение.

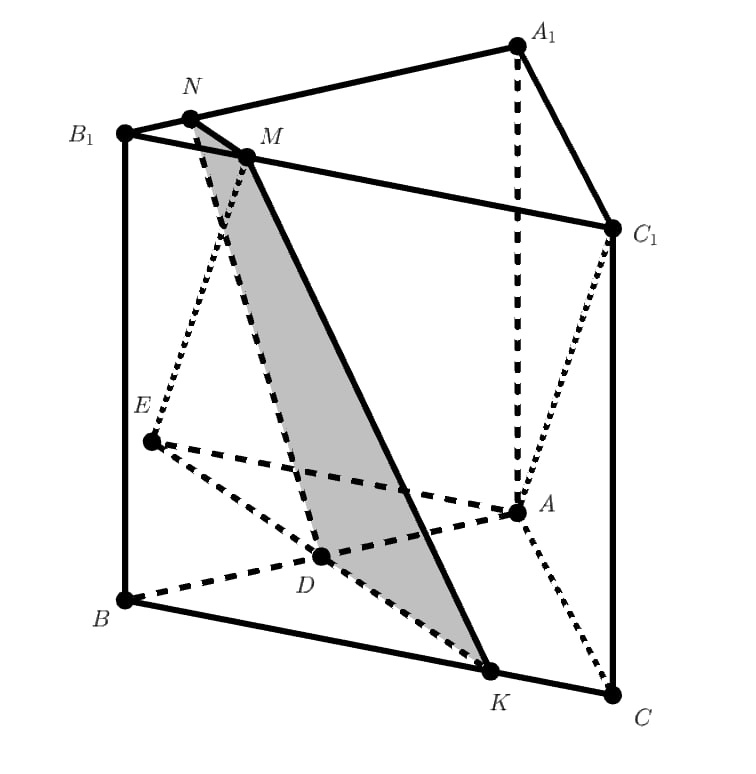
Найдём площадь проекции сечения на плоскость основания призмы. Обозначим сторону основания через . Тогда . Пусть — проекция точки на основание . Пусть — проекция точки на основание . Поскольку и параллельны, то , и . Проекцией сечения на плоскость основания является трапеция , её площадь

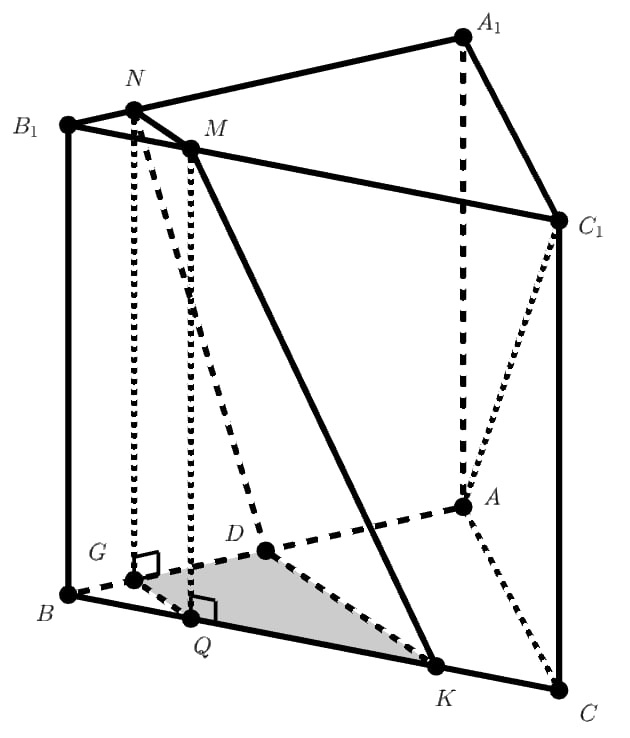
Найдём косинус угла наклона плоскости сечения к плоскости основания призмы. Расстояние от прямой до плоскости сечения равно расстоянию от точки до плоскости сечения, которое, в свою очередь, равно расстоянию от точки до плоскости сечения (так как , принадлежит плоскости сечения).

Построим плоскость проходящую через точку и перпендикулярную линии пересечения основания и плоскости сечения ( и перпендикулярны ). Проведем прямую перпендикулярную , тогда расстояние равно

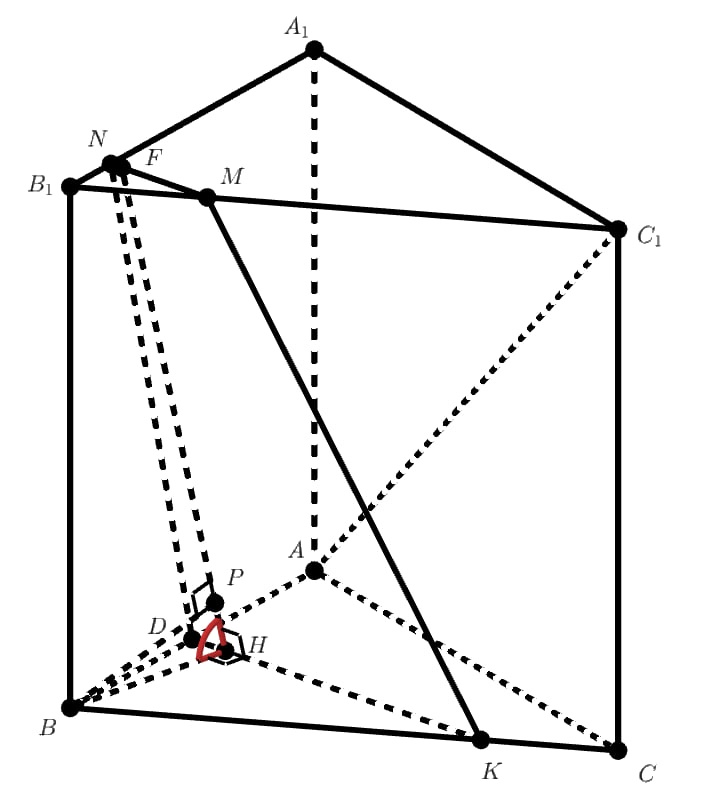
Угол наклона плоскости сечения к плоскости основания равен углу . Находим:

В треугольнике имеем

Итого по теореме о площади ортогональной проекции